在庫管理の基本的な動きを図１・１に示します。
①顧客から注文が入ります。
②注文に応じて（商品、数量、納期、、）出荷します。
③発注条件（定期、定量、定件）に合わせて、発注します。
④納入リードタイム（以下、納入LT）後に入庫されます。
これで在庫量が元の数量に戻ります。このサイクルが繰り返されます。
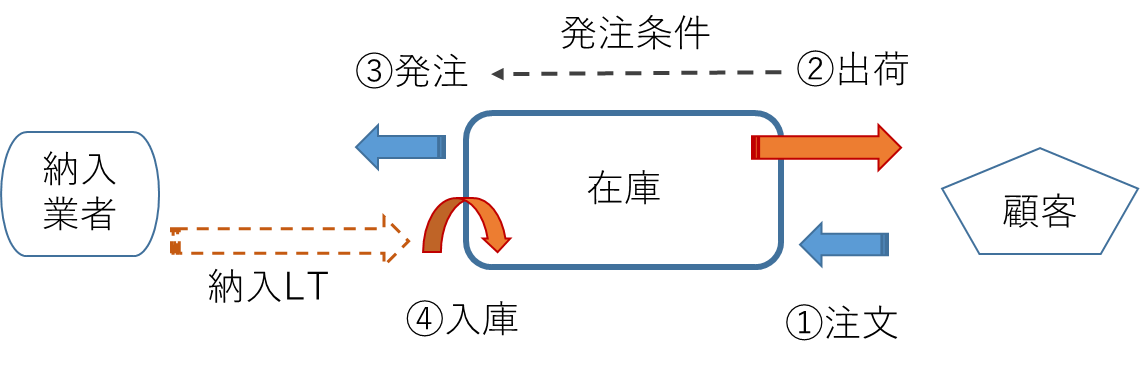
図１・１ 在庫流動の基本的な動き
在庫の動きを捉えるための基本要素は次の通りです。
＊件数/時間
ある時間に来る注文の件数（購買客数、、）です。通常、１日に何件とか１週間に何件とか、現場の作業環境に合った時間で集計しています。これが「件数/集計時間」です。在庫補充には通常、納入LTという時間がかかります。在庫管理では、納入LT間の需要を知る必要があります。その時使うのが「件数/納入LT」です。
＊数量/件
１件の注文の数量です。数量の単位はSKU（Stock keeping Unit;在庫管理単位）です。
＊発注方法
発注方法は、次の３通りあります。
①定期発注；予め決めた発注サイクル
②定量発注；出荷数量が予め決めた量に達した時
③定量発注；予め決めた受注件数に達した時
発注量は発注後、次の発注が行われるまでに出荷した数量です。
定期発注は発注毎に発注量と件数が変動します。定量発注は発注間隔と件数が変動します。定件発注は発注間隔と発注量が変動し、不定期不定量発注となります。
このような在庫の動きをモデル化したのが「在庫流動モデル」です。「在庫流動モデル」の基本は“出荷した分だけ補充発注する”ですが、“消費した分だけ補充する”という“かんばん方式”の基本と共通します。下記のように、基本要素も共通しています。
＊かんばん１巡時間 → 納入LT
＊かんばん回転枚数/かんばん１巡時間 → 件数/納入LT
＊収容数/箱 → 数量/件
＊消費数/かんばん１巡時間 → 需要/納入LT
“かんばん方式”では「かんばん回転枚数/かんばん１巡時間」も「収容数/箱」も定数ですが、「在庫流動モデル」では「件数/納入LT」も「数量/件」も確率変数となります。定数や確率変数を次のように表すことにします。
[・・] ；定数
（・・） ;確率変数
｛・・｝ ;合成確率変数
（（・・））；従属確率変数
在庫流動方程式は次のようになります。
[初期在庫]＝｛補充在庫｝＋（（実在庫））
＝｛発注量｝＋｛需要/納入LT｝＋（（実在庫））
＝｛発注量｝＋｛（数量/件）＊（件数/納入LT）｝＋（（実在庫））
＝[流動在庫]
[流動在庫]のイメージは図１・２のようになります。
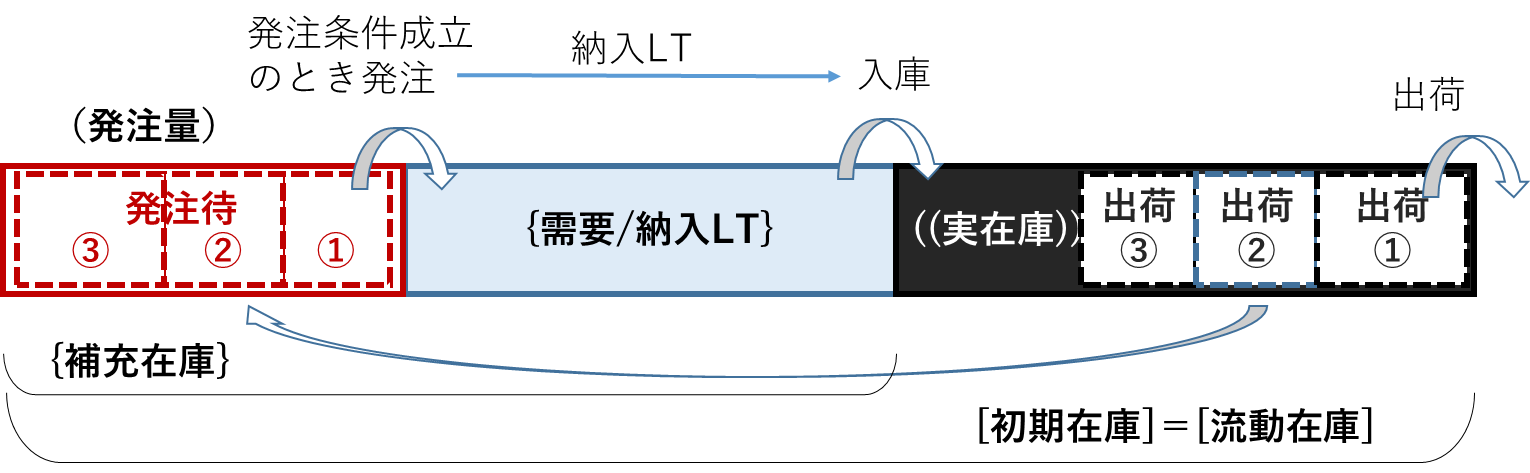
図１・２ [流動在庫]のイメージ
「適正在庫」は、｛補充在庫｝の分布とその累積確率カーブから求めます。図２・１をご覧ください。例えば、累積確率が９０％の在庫数量は３１個、９５％は３４個、９９％は４１個です。この累積確率が在庫管理ではサービス率となります。つまり、９０％のサービス率が必要ならば[初期在庫]を３１個、９５％のサービス率が必要ならば３４個、９９％のサービス率が必要であれば４１個の[初期在庫]が必要だ、ということになります。必要となるサービス率に対する「適正在庫」が[初期在庫]となります。
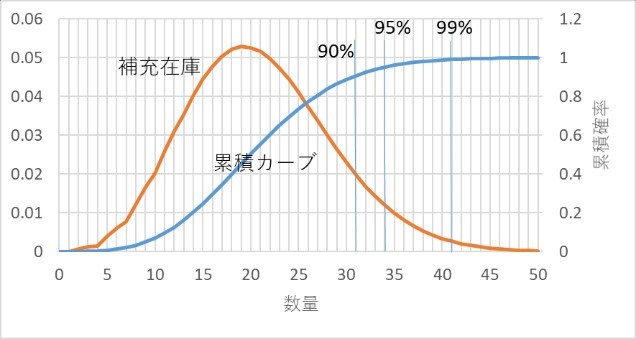
図２・１ サービス率（累積確率）と適正在庫との関係
「在庫流動方程式」から、｛補充在庫｝は次のようになります。
｛補充在庫｝＝｛発注量｝＋｛需要/納入LT｝
＝｛発注量｝＋｛（数量/件）＊（件数/納入LT）｝
｛発注量｝は発注方式によって異なりますので、ここでは、発注方式に共通な｛需要/納入LT｝を（数量/件）と（件数/納入LT）を合成して求めてみます。合成方法として、「分布形状アプローチ」と「数理アプローチ」の２つの方法があります。
コンビニでのボトル茶の販売を例にします。次のように読み替えます。
（件数/納入LT） → （客数/納入LT）
（数量/件） → （買上数/件）
｛需要/納入LT｝ → ｛買上数合計/納入LT｝
（客数/納入LT）がポアッソン分布、(買上数/客)がガンマ分布に従うとします。
ボトル茶を買う客は１日、平均２人来るとします。発注してから商品棚に並ぶまでの時間、「納入LT」は３日とします。先ずは簡単な条件で考えてみます。客は必ず１本しか買わないとしましょう。このとき、「納入LT」３日間の買上数合計の分布はどのようになるかを考えてみたいと思います。
客数は１日平均２人ですので、３日間では平均６人の客が来ます。つまり、来客数の確率分布は平均６のポアッソン分布となります。来客３人の確率は０．０９、来客４人の確率は０．１３、来客５人は０．１６、、、という具合です。その確率分布を図２・２の左側上に示します。
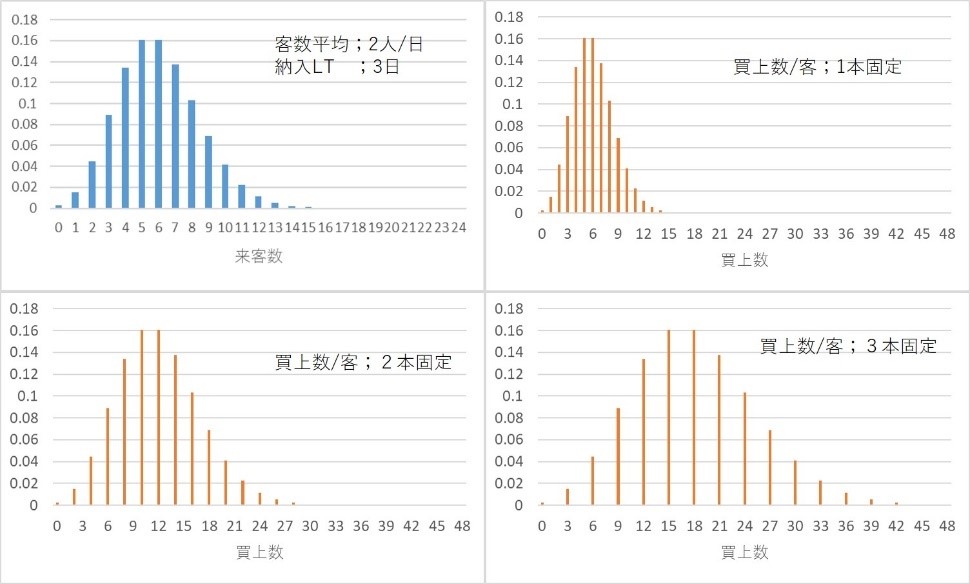
図２・２ 買上数/客が１本、２本、３本の時の｛買上数合計/納入LT｝の分布
では、「納入LT」３日間の買上数合計はどうなるでしょうか。客は全員、ボトル茶１本しか買いませんので、来客数と買上数合計はまったく同じになります。買上数３本の確率は０．０９、買上数４本は０．１３、５本は０．１６、、、となります。図２・２の右側上の図を参照ください。
客が全員、２本買った場合はどうなるでしょうか。図２・２の左側下に示すようになります。例えば客数が３人であれば買上数は、２（本）＋２（本）＋２（本）＝６（本）、客数が４人であれば、２（本）＋２（本）＋２（本）＋２（本）＝８（本）、５人であれば１０本、、、となり、買上数６本の確率は０．０９、８本の確率は０．１３、１０本は０．１６、、、となります。
客が全員、３本ずつ買った場合は図２・２の右側下のような分布になります。客数が３人であれば、３（本）＋３（本）＋３（本）＝９（本）、４人であれば、３（本）＋３（本）＋３（本）＋３（本）＝１２（本）となります。買上数９本の確率は０．０９、１２本の確率は０．１３、１２本では０．１６、、、となり、確率分布形状は(買上数/客)が大きくなるに伴い右方に広がるようになります。
(買上数/客)が変動するとどうなるでしょう。バラツキの分布はすでに説明しましたように、ガンマ分布を使います。
（買上数/客)の平均は３本、変動係数を０．２５としてみます。客が１人のときは平均３、変動係数０．２５のガンマ分布となります。客が２人のときは、平均３、変動係数０．２５のガンマ分布に従う確率変数の和の分布となります。客が３人ではガンマ分布に従う確率変数３つの和の分布となります。
複数のガンマ分布の和はどのような分布になるのかを確認しておきます。ガンマ分布は、既述の通り、再生性があります。つまり、ガンマ分布に従う確率変数の和の分布もガンマ分布となります。
（買上数/客）の平均が３本で、変動係数が０．２５のとき、客が１人、２人、３人、、、８人それぞれの買上数合計の分布の一例を折れ線グラフで図２・３に示します。客数が多くなるに従い分布の山の高さが低くなり、すそ野が広くなります。各山状の分布の面積が確率を表すことになりますが、いずれの分布も確率は１となります。
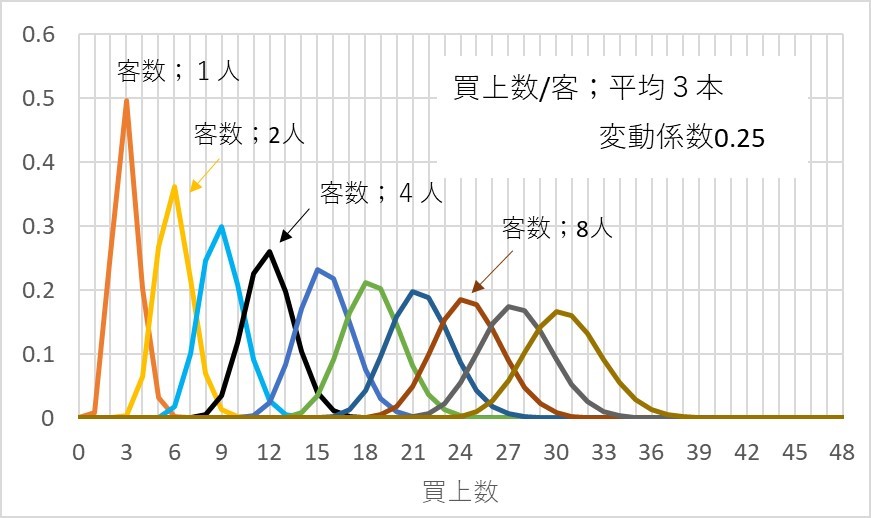
図２・３ 客数と買上数合計の分布
次に、｛買上数合計/納入LT｝の分布はどうなるか考えてみます。(買上数/客)平均３、変動係数０．２５、「納入LT」３日のとき、｛買上数合計/納入LT｝の分布は図２・４右側下に示すような全体にかぶさる山状のカーブになります。
山状のカーブの下方に①、②、③、、、と小さな山状のカーブがたくさんあり、これらの小さな山を全部集計したものが｛買上数/納入LT｝の確率分布となります。
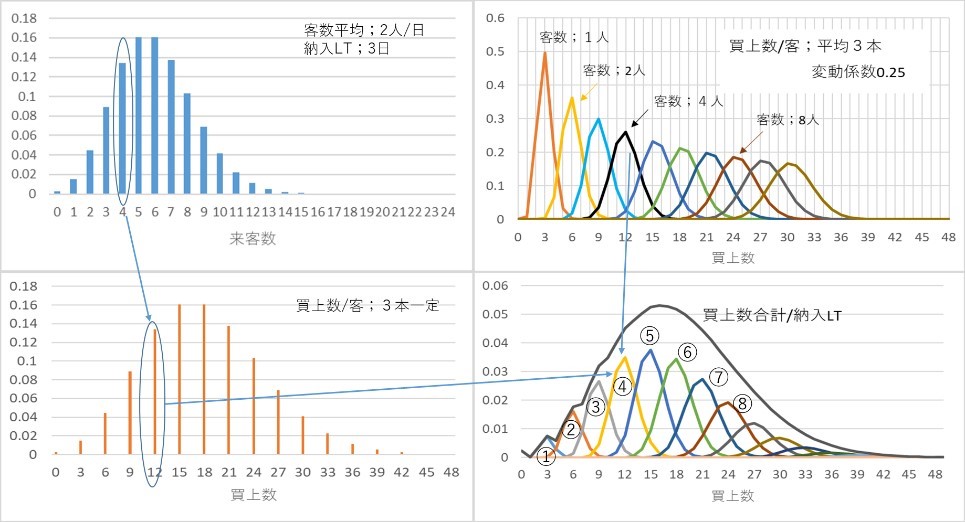
図２・４ （客数/日）平均２人、（買上数/客）平均３、変動係数０．２５、「納入LT」３日のときの｛買上数合計/納入LT｝分布
｛買上数合計/納入LT｝の分布の成り立ちを図２・４に示します。④の分布を例にとります。④の分布は客数が４人のときの買上数の分布です。右側上のグラフでみるとわかると思います。（買上数/客）が３本一定の場合は、左側下のグラフのように買上数１２本の位置に棒がきます。買上数１２本の発生確率は０．１３ですので、右側上の来客数が４人の分布に０．１３が乗じられ、右側下の④の分布となります。
｛買上数合計/納入LT｝の確率分布は、様々な形状となります。平均値が大きいときは正規分布に似ていますが、小さい時はゼロ側に押しつぶされたような非対称な形状となります。
最初の「納入LT」の間に受注する数量をみてみます。「納入LT」間に来る、初めの注文の数を Q１(１) 、次の注文数量をQ１(2)、、、「納入LT」での最後の注文がN１番目となり、その数量をQ１(n１)とします。その間の需要D1は次の式で表されます。
-----式①
これは「納入LT」間に、N１件の受注があり、その間の需要はD１であることを示します。これが最初の「納入LT」とします。
同様に２回目の「納入LT」での需要D２は次のようになります。
-----式②
３回目の「納入LT」での受注数量、そしてm回目の「納入LT」での需要は次のようになります。
-----式③
┇
-----式ⓜ
表２・１に「納入LT」での需要、受注件数と（数量/件)を示します。「納入LT」順番１が式①、順番２が式②、順番３が式③、順番mが式ⓜに相当します。
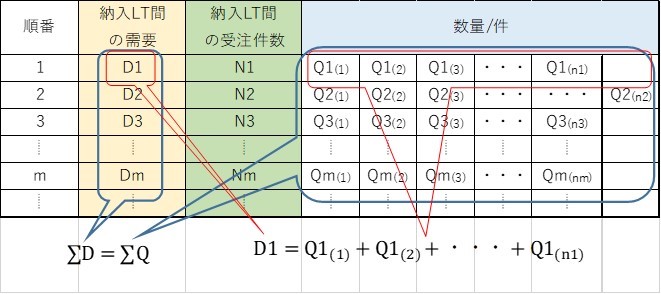
表２・１ 「納入LT」ごとの受注数量、受注件数と数量/件
これらの式から、Qの平均Qバー、その分散Vqおよび Nの平均Nバー、その分散Vnを使って、Dの平均DバーおよびDの分散Vd の関係を表す方程式を導き出します。
初めにDバーとNおよびQの関係式を検討します。表２・１と式①～式ⓜをご覧ください。左辺の合計と右辺の合計を次のように表します。
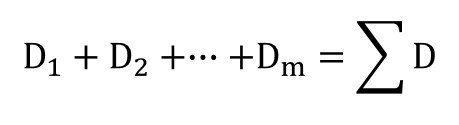
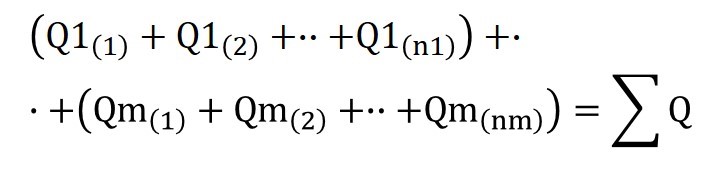
左辺の合計と右辺の合計は同じですので、
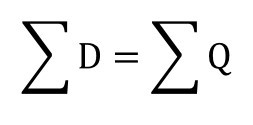-----式④
となります。（数量/件)の平均QバーはQの総計を受注件数の総数で割って、
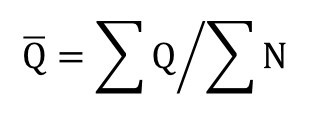-----式⑤
となります。一方、｛需要/納入LT｝の平均 Dバー は シグマD をDのデータ数mで割って、次のようになります。
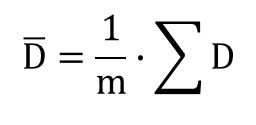
式④と式⑤から、
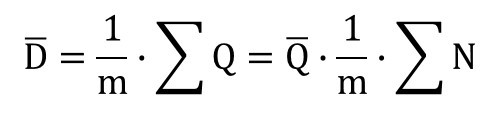
となります。Nの合計をmで割ったものがNの平均なので、次のようになります。
次に、分散の式を求めます。aを定数、確率変数Xの分散をV[X]として、次の分散公式を利用します。
分散の公式
V[X+Y]=V[X]+V[Y]
但し X、Yは独立。これらの公式の証明は省略します。
Qの分散 Vqをゼロに近づけると、
となり、QはQの平均値 Qバー となり、そのときの需要 Dｑバーは、次のようになります。
Qバー は定数、Dｑバー とNは確率変数なので Dqバーの分散 V[Dqバー] は、公式[１]から次のようになります。
次に、Nの分散 Vnをゼロに近づけますと、
となり、NはNの平均値 Nバー となります。このときの需要 Dｎバー は、次のようになります。
Dnバー の分散 V[Dnバー] は公式[２]から、次のようになります。
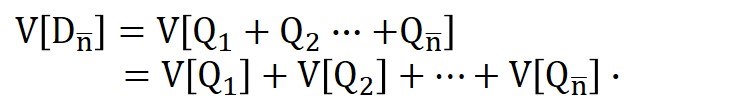
（数量/件)Qは同一母集団に属しますので、
となり、次のようになります。
V[Dqバー]とV[Dnバー]は分散の加法性が成立するとして、Dの分散 Vdは、次のようになります。
まとめると、次のようになります。
------式２－１
------式２－２
｛需要/納入LT｝の平均は式２-１、分散は式２-２で求めることができます。
「適正在庫」を求めるためには｛補充在庫｝の分布を知る必要があります。｛補充在庫｝は、
｛補充在庫｝＝｛発注量｝＋｛需要/納入LT｝
です。｛需要/納入LT｝は発注方法に関係なく同じですが、｛発注量｝は発注方法により異なりますので、発注方法ごとに、｛発注量｝がどうなるか、｛補充在庫｝がどうなるかをみてみます。
定件発注方式は注文（購買客）が予め決めた件数（客数）に達した時、その間に受注（売上）した分を補充発注する発注方法です。
図３・１に｛発注量の｝の時系列変化の一例を示します。定件数は５です。５人目の客が購買した時に発注しますので、来客が５人ごとにゼロになります（水色）。橙色は（数量/件）（一人当たりの買上数）を示しています。客数に（数量/件）を累積すると灰色の｛発注量｝となります。
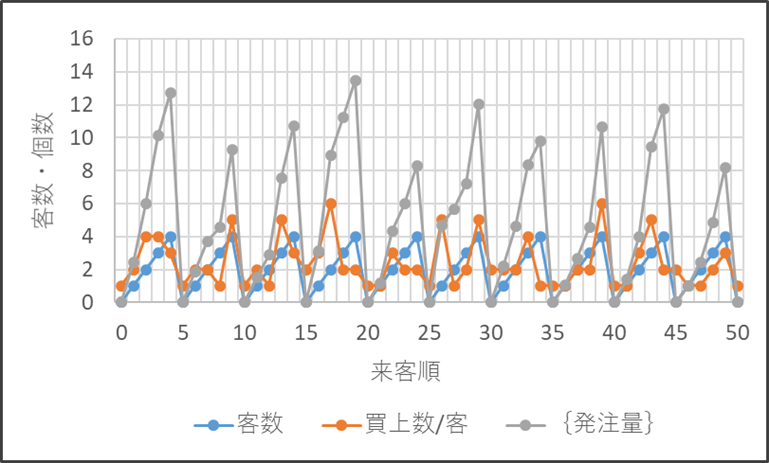
図３・１ 客数、買上数/客、｛発注量｝の時系列変化
図３・２は客数、買上数/客、｛発注量｝の確率分布を示しています。
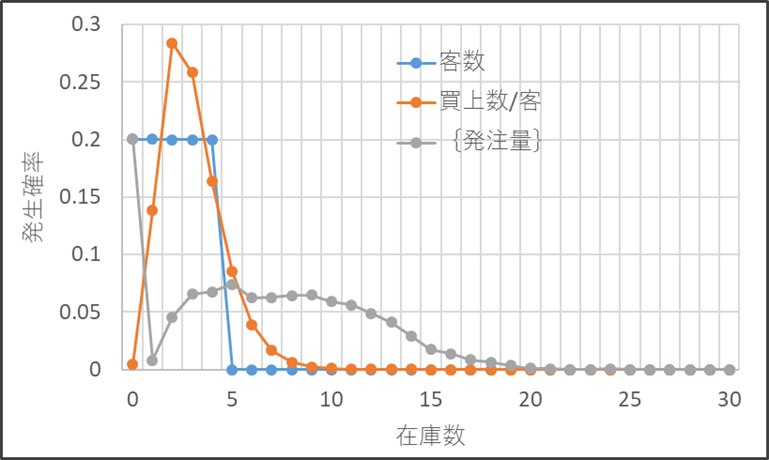
図３・２ 客数、買上数、｛発注量｝の確率分布
定件数をNcとして、｛発注量｝の平均OQバー、分散Voqは次のようになります。
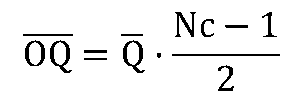
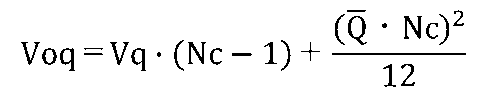
｛補充在庫｝の平均と分散を求める式は次の通りです。
｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の確率分布の一例を図３・３に示します。
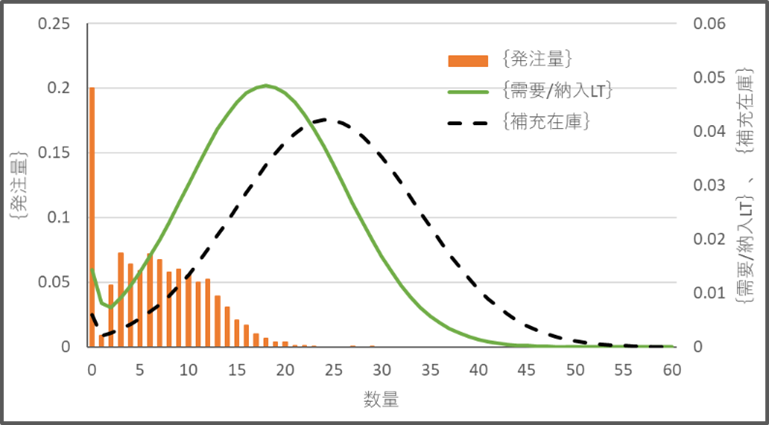
図３・３ ｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の確率分布の一例
定期発注方式は一定時間（発注サイクル）ごとに、その間に受注（出荷）した分を補充発注する発注方法です。
一定時間に来る注文件数の推移は、鋸歯状になります。（数量/件）はバラツキます。ここではガンマ分布を使っています。鋸歯状の件数に（数量/件）が合算されて、｛発注量｝となります。図４・１は、左側のグラフが件数、（数量/件）、｛発注量｝の時系列推移、右側のグラフはそれぞれの確率分布を示しています。
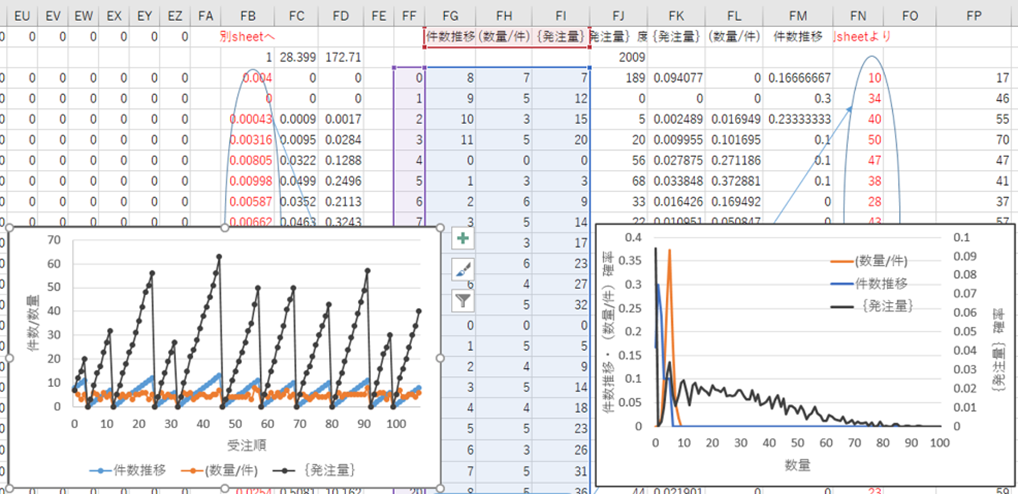
図４・１ ｛発注量｝の分布形状の一例
発注サイクル間の件数の平均をNyバー、分散をVnyとして、｛発注量｝の平均OQバー、分散Voqは次のようになります。
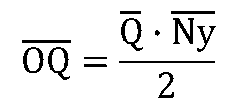
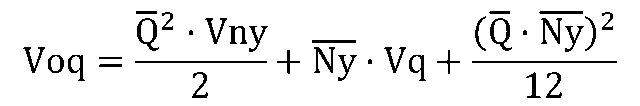
｛補充在庫｝の平均と分散は次のようになります。
定期発注の｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の一例を図４・２に示します。
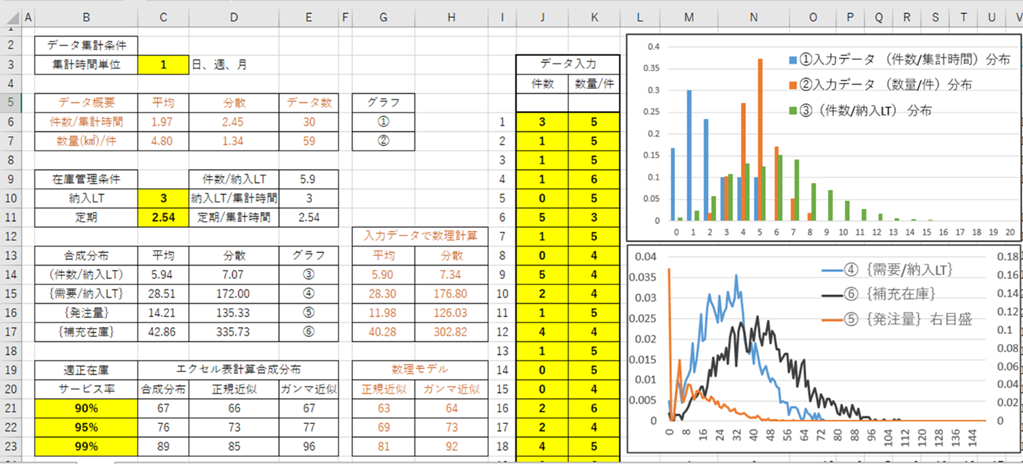
図４・２ 定期発注の｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の一例
定量発注方式は受注量（出荷量）が予め決めた一定量に達した時点で補充発注する方法です。定件発注や定期発注と異なる点は“発注遅端数”が生じることです。図５・１参照。
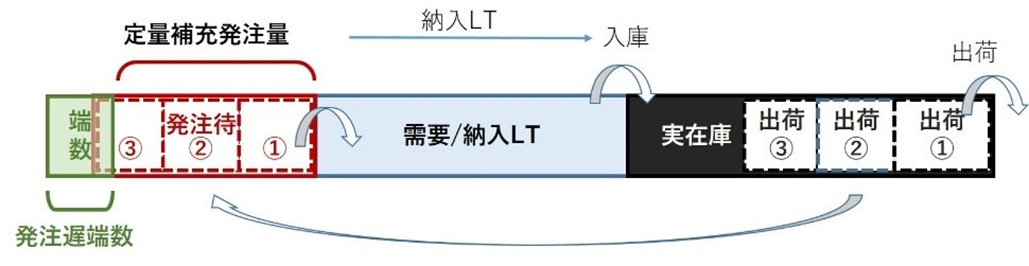
図５・１ 定量発注での[流動在庫]の一例。発注遅端数が生じる
図５・２は定量発注量（赤点、５０）、（数量/件）、｛発注量｝の時系列変化を示したものです。
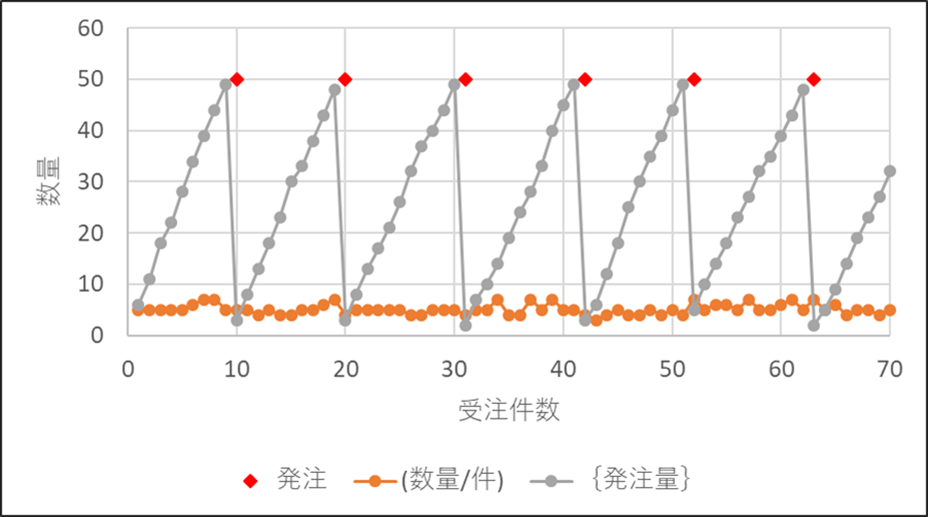
図５・２ 定量発注での｛発注量｝の時系列変化
定量をOcとして、｛発注量｝の平均OQバー、分散Voqは次のようになります。
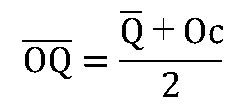
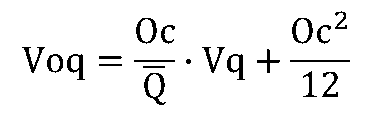
｛補充在庫｝の平均と分散は次のようになります。
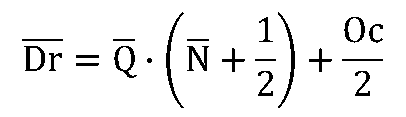
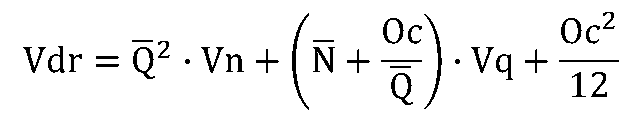
｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の確率分布形状の一例を図５・３に示します。
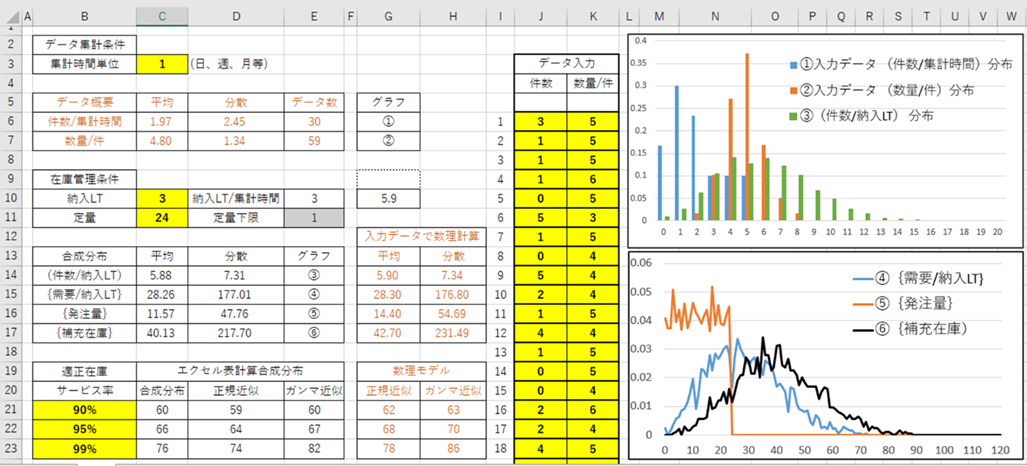
図５・３ 定量発注での｛発注量｝、｛需要/納入LT｝、｛補充在庫｝の一例
図６・１に分布形状アプローチの構成とその流れを示します。
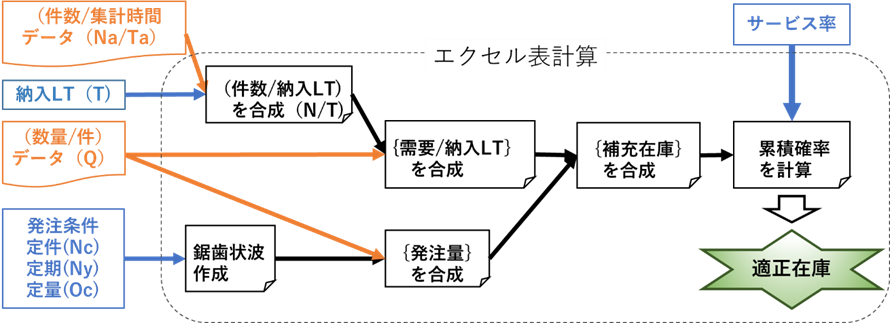
図６・１ 分布形状アプローチの構成と流れ
図６・２に数理アプローチの構成とその流れを示します。
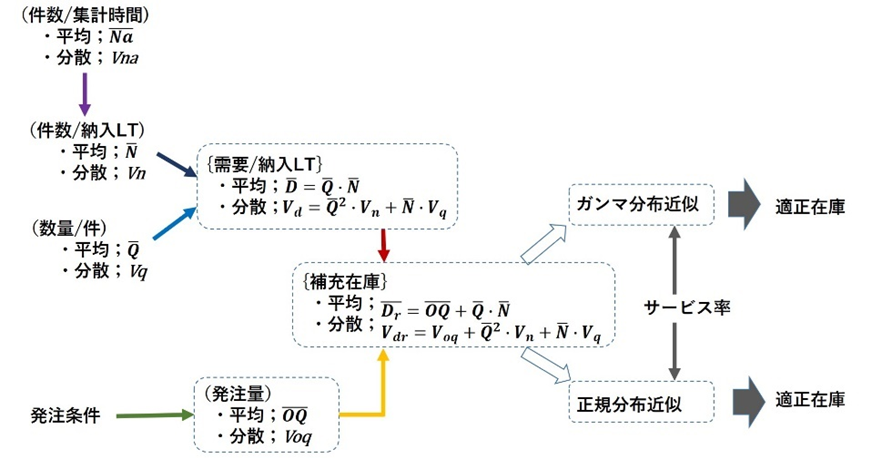
図６・２ 数理アプローチの構成と流れ
表６・１に数理アプローチで使う｛補充在庫｝の平均と分散の数式を示します。
表６・１ ｛補充在庫｝の平均と分散を求める数式
ここまでは、在庫の流動は「在庫」～「在庫」を想定してきました。”かんばん方式”で言えば“引取かんばん”に相当します。本章では、生産ラインと直結した製品倉庫の在庫管理について検討したいと思います。”かんばん方式”の“仕掛けかんばん”に相当します。
図７・１に生産ラインと直結した製品倉庫のイメージを示します。製品倉庫から出荷されますと、発注条件（定期、定量、定件）に従ってまとめた数量；｛発注量｝の生産指示を出します。生産指示は一旦、投入計画表にプールされます。生産ロットには投入予定日、インベントリ―ランク等の情報も付けられます。その条件で生産ロットの投入の優先度を調整することができます。
｛補充在庫｝は、（投入計画表＋生産ライン仕掛）となります。[流動在庫]は｛補充在庫｝に((実在庫))を加えた在庫です。この場合も[補充在庫]は一定になります。インベントリ―ランクの情報を使って、生産ロット（生産品）間の相対的な優先度を判断し、優先制御することもできます。
顧客からの注文は即納の場合もあれば、納期指定の場合もあるなどいろいろです。「在庫流動管理」をベースにした「自動需要追従生産」は即納を基準に機能するように構築されています。出荷予定表に登録された顧客からの注文は即納でも顧客納期があっても在庫は確保されます。出荷されれば、生産指示が出され生産予定表に追加され、需要に追従した生産が継続されることになります。
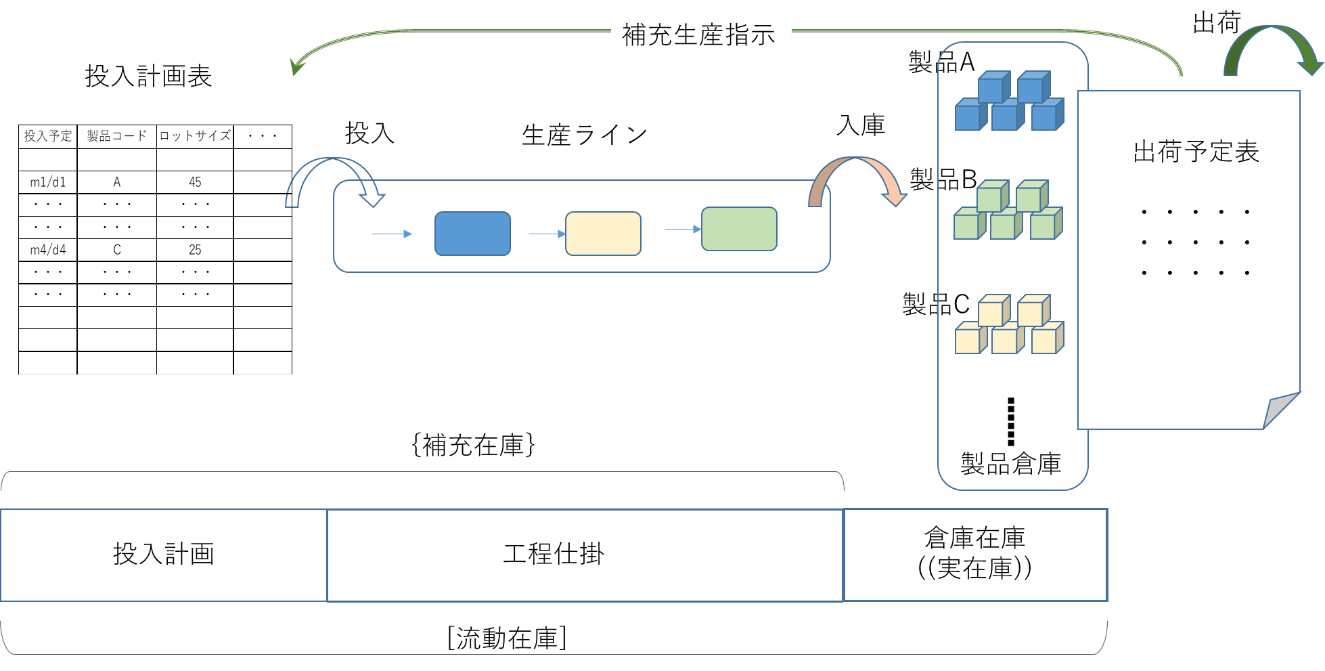
図７・１ 需要に自動追従する生産ラインのイメージ
「在庫流動モデル」の中に生産ラインが組み込まれることにより、在庫流動管理と生産管理が一体化され、需要をトリガーとした投入計画（生産計画）の自動生成、優先度の自動調整などが可能となり、第４次産業革命の時代の生産ラインの在り方を問う、ひとつの方向性を示すのではないか、と考えます。