在庫基準から需要基準へ

１、在庫管理;なぜうまくいかないのか

大量生産が始まった１９世紀後半～２０世紀中ごろまで、景気循環はあったものの、おおむね売り手市場。いかに効率よく生産量を増やすか、いかにスムーズに部材を調達、供給するかが課題でした。そんな背景で在庫管理の仕組みも形づくられたと考えられます。

ある量まで減ったら買い足す。日常生活でも常備品はそうします。発注点方式の原型です。発注してすぐ納入されるものはいいのですが、、中には足の長い資材もあります。３カ月とか４カ月とか、中には６カ月以上かかるものも、、。これに発注点方式を適用すると、在庫の山と欠品に悩まされることになります。

先々使うであろう量を定期的に補充発注する方法が考案されました。本来なら生産計画を基に資材所要量を計算すればいいのですが、先々の生産計画など当てになりません。資材は資材の責任で予測し、発注することになります。定期不定量発注方式の原型です。

在庫管理は、在庫のあるところで必要になります。在庫のあるところと言いますと、資材倉庫の他に、工場の製品倉庫、地域・物流倉庫、問屋、小売店、工場内にある半製品倉庫、生産ラインの中にある仕掛、外注からの受け入れ倉庫、、、。これらの連鎖がサプライ・チェーンになるわけですが、、、。

工場の資材倉庫の管理から始まった在庫理論は現在も尚、健在です。これを古典在庫論と呼んでおきます。この古典在庫論は、現代の多様化した在庫形態に適用できるのか。結論から申し上げますと、答えは「否」。どこに問題があるのか。原因を上げればきりがありませんが、ここでは簡単に、「非対称性」と「適正在庫の曖昧性」の２点について、触れておきます。

＜非対称性＞

図１をご覧ください。Aで在庫管理が行われいます。顧客から注文を受けて出荷します。AはBに発注し在庫を補充します。AからBに発注するときは、定期不定量発注、定量不定期発注、いずれの場合も、発注時刻とその時の発注量を記録します。B側は、Aから来た注文の受注時刻と受注量を記録します。Aも顧客から注文を受けていますので、案件ごとに受注時刻と受注量を記録します。商取引ですのできちんと行われていなければなりません。これを在庫管理のテーブルに持ってくるとどうなるか。

図１　在庫管理の基本要素

在庫管理の基本は「出」に合わせて「入り」を調整・管理することですので、「出」と「入り」は同じ物差しで測らなければなりません。「出」は需要です。需要をコントロールすることはほとんどできませんので、受け入れるしかありません。ですから、バラツキ範囲を含めて、需要の大きさを知ることが重要です。

在庫管理で需要の大きさを予測するとき、例えば、調達リードタイムが2カ月であれば2カ月先までの需要を予測します。そのとき、受注件数と一件当りの受注量を分けて予測しているでしょうか。古典在庫論では、そうは教えていません。2カ月先までの需要見込はXXX個。(period)　件数が何件で一件当りの受注量は何個、、、だから需要総量の平均はYYY個、バラツキはZZZ、なんて見積をやっているところ、あまり聞きません。

発注するときは、発注間隔や一件当りの発注量をすごく気にしますが、需要をみるときは大雑把。つまり、「出」と「入り」で物流を違った眼鏡でみているわけです。これを「非対称」だ、と、、。

「えっ！それって、何が問題なんですか？」

ある期間の受注件数の平均が40件、一件当りの平均受注量が5個の場合と受注件数の平均が10件、一件当りの平均受注量が20個の場合、その期間の受注量の平均は200個でどちらも同じです。ではバラツキはどうでしょうか。前者と後者の受注件数の変動係数は同じ、前者と後者の一件当り受注量の変動係数も同じとして、両者のバラツキは同じにはなりません。ドーンと一度に受注するよりは多数回に分けて注文をもらう方が在庫は少なくて済むということは直観的にわかると思います。つまり、ある期間の受注量のバラツキを正しく捉えるためには、受注件数と一件当りの受注量を別々に捉える必要があります。

サプライ・チェーンは、図１に示すような在庫管理ユニットのつながりで構成されています。そこを物品が滞留、流動します。「出」と「入り」を異なった視点でみれば、言い方を変えれば、「出」と「入り」の対称性がなければ、在庫管理ユニット間のつながりがスムーズにいかなくなります。

物理学の視点からも対称性のある、なしは意外に重要です。例えば、力学の方程式は座標軸を平行移動しても回転しても変わりません。宇宙のかなたでも成り立ちます。物理法則は対称性があればあるほど普遍的である、対称性があればあるほど美しいと言われております。在庫補充の仕組みも物理現象ですから、対称性があればあるほど普遍的である。逆に対称性がないということは、古典在庫論の適用範囲が狭いということを示唆しているのではないでしょうか。

＜適正在庫の曖昧性＞

図１を見ながら、在庫の流れを時系列で少し詳しく、みてみますと、受注→出荷→在庫減→発注待ち→発注→発注残→納入→入庫、、こんな感じでしょうか。受注がトリガーとなり、出荷、発注、入庫というイベントが連鎖的に起きます。イベントごとに在庫の状態が変わりますので、それぞれの在庫状態にある数量も変化します。

留意しておきたいことは、倉庫にある実（現物）在庫だけではなく、発注待ちや発注残という状態の在庫も、ほぼ常時存在し、その量も時には実在庫を上回るということです。そして、それぞれの状態にある在庫量はイベントごとに増減します。

ところが、古典在庫論では、維持すべき「適正在庫」が、具体的に、何を指すのか、いまいちはっきりしません。中には、発注残も含めて「適正在庫」を説明する例もありますが、多くは、実（現物）在庫を「適正在庫」に結び付けて説明しています。 いずれにしましても、それぞれの状態にある在庫量は変動しますし、どれとどれかを合算してもバラツキます。

在庫管理では管理基準として「適正在庫」は最も重要なもののひとつです。それが、実態では、どの在庫を持って「適正在庫」と照合すればいいのか、曖昧です。

２、在庫管理にもDXの波

最近DX（Digital Transformation）の動きが活発になってきました。このままだと、古典在庫論との乖離はますます広がっていくのではないか、と危惧します。DXへの方向転換は待ったなし、です。

古典在庫論の問題が、「非対称性」と「適正在庫の曖昧性」にあると看破すれば、対策の方向性は見えてきます。この2つを解決する方策は意外に簡単です。

出荷（受注）量＝発注量

とします。”消費した分だけ発注する”という”かんばん方式”と同じです。出て行った分だけ補充しますので、循環する在庫量は、常に一定です。これが「適正在庫」になりますので「適正在庫」は固定値となります。

発注するタイミングですが、最も単純な方法は、出荷時に発注することになりますが、出荷が頻繁な場合、発注回数も増えて作業が煩雑となり、必ずしも合理的ではありません。実務を考慮して、定期発注、定量発注、定件発注の条件で発注タイミングを設定します。

定期発注は、従来と同じく発注サイクルごとに発注しますが、発注量はその間の出荷量と同じ量を発注します。定量発注は出荷量が予め決めた数量に達した時、その定量を発注します。実在庫に発注点を設定するわけではありません。定件発注とは、受注件数が予め決めた件数に達した時、その件数での受注量（出荷量）を発注する方法です。

いずれの発注方法でも「適正在庫」は固定値となります。これで、「非対称性」と「適正在庫の曖昧性」が修正されることになります。

３、在庫補充の基本的仕組み；在庫流動モデル

「非対称性」と「適正在庫の曖昧性」の問題を解決した、新たな在庫補充の仕組みを「在庫流動モデル」と呼んでおきます。

図２は簡略化した「在庫流動モデル」の模式図です。補充発注方法は前述しましたように、次の３つがあります。

*定期発注
*定量発注
*定件発注

それぞれの発注方法の特性については、後ほど、触れます。

ここでは在庫流動の大まかな動きを確認しておきます。在庫状態は、出荷、発注、入庫などのイベントごとに移り変わり、それぞれの在庫数量は変動しますが、循環する全体の在庫数量は一定です。

この全体の在庫を[流動在庫]と呼ぶことにします。常に一定なので[ ]を付けておきます。[流動在庫]は｛補充在庫｝と((実在庫))で構成されます。｛補充在庫｝は｛発注量｝と｛需要/納入LT｝が合算されたものです。｛需要/納入LT｝は(件数/納入LT)と(数量/件)が合算されたものです。この関係を式で示せば、次のようになります。

[流動在庫]＝｛補充在庫｝＋((実在庫))
    ＝｛発注量｝＋｛需要/納入LT｝＋((実在庫))
    ＝｛発注量｝＋｛(件数/納入LT)*(数量/件)｝＋((実在庫))

  [・・]    ；定数
（・・）    ;確率変数
｛・・｝    ;合成確率変数
((・・))    ；従属確率変数

この式を「在庫流動方程式」と呼んでおきます。

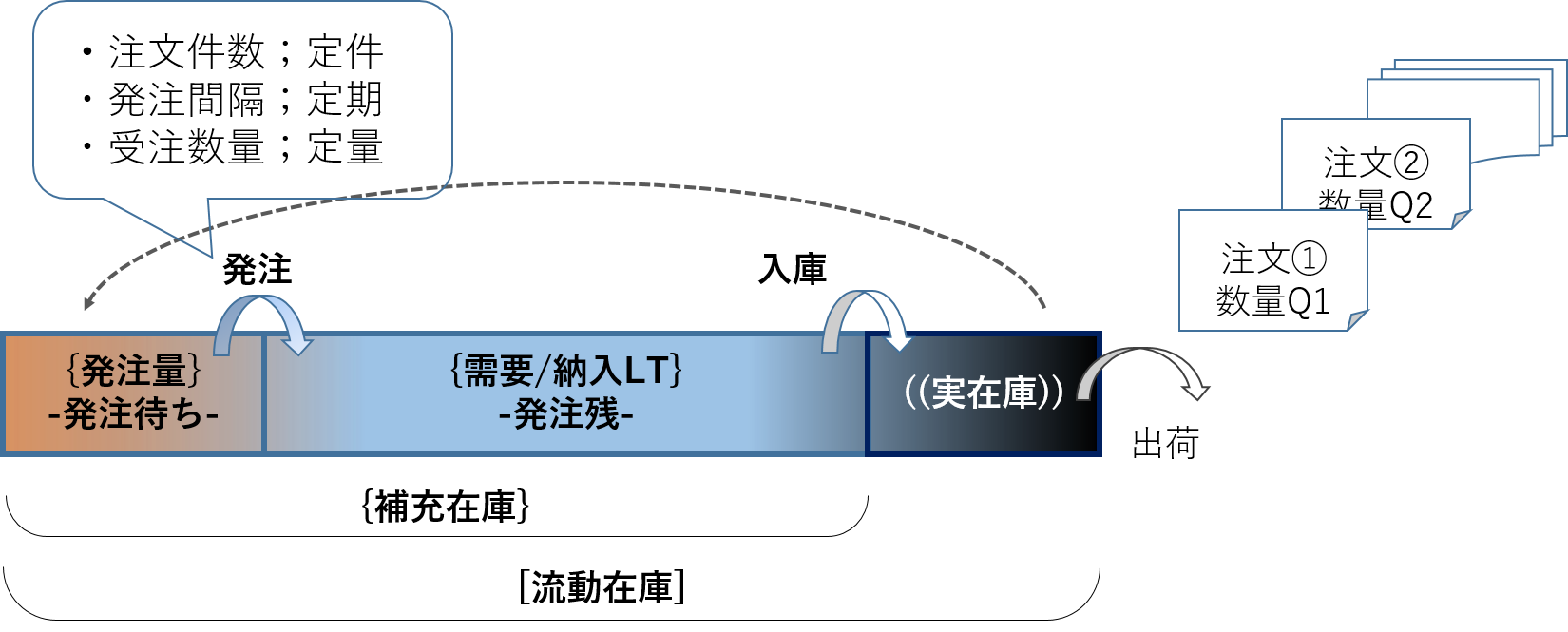
図２　在庫流動モデル

４、在庫流動管理

「在庫流動モデル」をベースに、需要をトリガーとして流動する在庫の動きを管理するために構築された在庫管理方法が「在庫流動管理」です。主な特徴は次の通りです。

＊出荷した分だけ発注して補充

”消費した分”だけ”発注”、という”かんばん方式”と同じ原理です。

＊[流動在庫]が常に一定

[流動在庫]が常に一定であることを利用して、異常の検知、優先度の判断、全体の在庫量把握など、様々な管理の基準として利用することができます。

＊((実在庫))＝０のときの｛補充在庫｝が「適正在庫」

「在庫流動方程式」から、((実在庫))がマイナスのときは欠品、プラスのときは余剰在庫を意味します。このことから((実在庫))＝０のときの｛補充在庫｝が「適正在庫」であると言えます。｛補充在庫｝は確率分布しますので、サービス率に等しい累積確率の数量が「適正在庫」となります。

＊「適正在庫」＝[流動在庫]＝[初期在庫]

「適正在庫」に等しい[初期在庫]を準備します。このとき、[流動在庫]は[初期在庫]と等しくなります。

＊ある期間ごとに「適正在庫」を見直す

ある期間、例えば１カ月ごととか、３カ月ごととか、その需要環境に応じて、「適正在庫」の見直し、再設定を行います。

＊需要の増減は常に監視

見直し期間内での需要の増減はありますので、常時監視します。ある範囲を超えたときは「適正在庫」を再設定します。

５、定量発注、定期発注、定件発注

「在庫流動管理」では定量発注、定期発注、定件発注の３つの発注方法があります。それぞれの「適正在庫」は、｛補充在庫｝の確率分布を求め、サービス率に等しい累積確率となる数量を見つけることで計算できます。

｛補充在庫｝は既述のように、｛発注量｝と｛需要/納入LT｝を合算したものです。

｛補充在庫｝＝｛発注量｝＋｛需要/納入LT｝

{需要/納入LT}はどの発注方法でも同じで、その平均と分散は次の式で求めることができます。

  ーーー式１

 ーーー式２

;件数/納入LTの平均、Vn；Nの分散
；数量/件の平均、Vq；Qの分散
;需要/納入LTの平均、Vd；Dの分散

｛発注量｝は発注方法で異なります。

＜定量発注＞

定量発注は、受注量（出荷量）が、あらかじめ決めた一定量;Ocに達した時に補充発注する方法です。{発注量}の平均と分散Voqは次のようになります

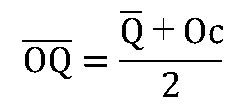
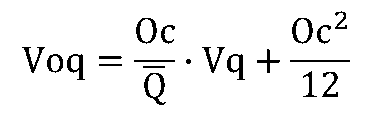
定量発注での｛補充在庫｝の平均と分散Vdrは次のようになります。

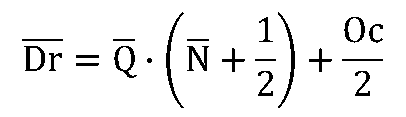
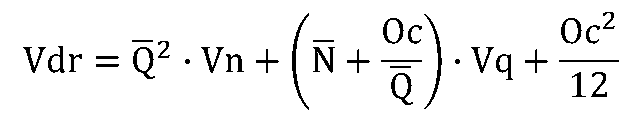
＜定期発注＞

定期発注はあらかじめ決めた一定時間ごとに、その間の受注量（出荷量）を補充発注する方法です。発注時間間隔（発注サイクル）での平均受注件数をとして、｛発注量｝の平均と分散、および｛補充在庫｝の平均と分散は次の式で表すことができます。

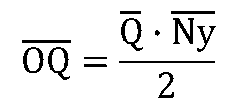
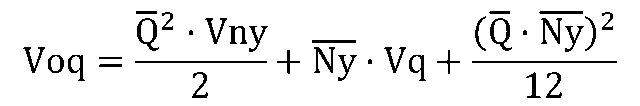
＜定件発注＞

定件発注は、受注件数が予め設定した件数に達した時に発注します。｛補充在庫｝の平均と分散は次のようになります。

６、納入リードタイムの変動がある場合

発注してから入庫されるまでの納入リードタイムが変動する場合、｛補充在庫｝は次のようになります。納入リードタイムの変動は｛発注量｝には影響はなく、｛需要/納入LT｝の分散を大きくします。その分散をVntとすると、Vntは次の式で求められます。

｛需要/納入LT｝の分散VdはVntが加算され、次のようになります。

７、在庫流動管理　まとめ

表７－１は「在庫流動管理」での「適正在庫」を算出するために必要となる｛補充在庫｝の平均と分散を求める数式の一覧表です。

黒字は｛需要/納入LT｝を、水色は｛発注量｝を、茶色は納入LTの変動の影響を示しています。

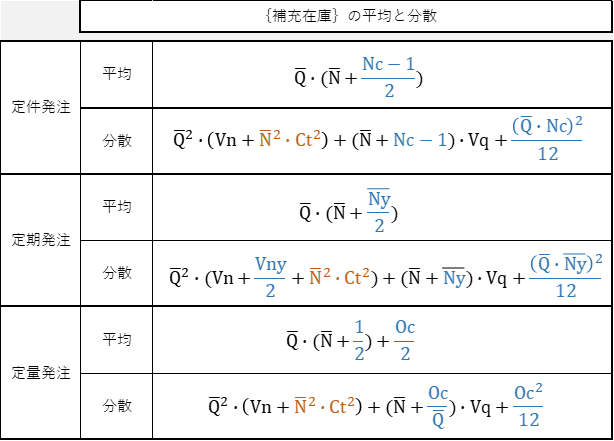
表7-1　在庫流動管理　｛補充在庫｝の平均と分散

８、在庫流動管理の導入

「在庫流動管理」は、在庫補充の仕組みを物理現象として捉え直した「在庫流動モデル」をベースに組み立てた在庫管理の方法です。現行の在庫理論に比べて格段に普遍性が高くなり、サプライ・チェーンのすべてに適用することができます。また、在庫管理の方法は簡単になり、現行からの移行も比較的容易に行うことができます。

現在、何らかの在庫管理を行っていることを前提に、「在庫流動管理」の導入について、概説しておきます。

① 対象SKU（Stock Keeping Unit）を選ぶ。
      比較的安定して流れているいるSKUを数点～十数点、選定する。
② 定量発注にするか定期発注にするかを決める。定量発注量や発注サイクルを設定する。特に事情がない限り、現行のままでOK。（現在、定件発注を行っているところはないと思います）
③ 「適正在庫」を設定する。新たにデータをとる必要はない。手持ちのデータを利用するか、経験的な数値でもOK。
④ 受注、発注、入庫等の作業は現行のままでOK。
⑤ 納入業者への連絡は必要に応じて行う。
⑥ 適用範囲を広げていく。
⑦ 管理サイクルを回し、定期的に、また必要に応じて「適正在庫」等を調整・改訂する。

「在庫流動管理」は動的生産管理（DPM）を支える重要な機能です。DPMの導入という視点からみますと、生産の上流から切り替えることが推奨されます。

一般的に、「在庫流動管理」の方が簡単ですので、現行方式からの移行もスムーズに行うことができます。在庫が少なくなる、欠品率が低下するなどの効果が比較的短時間に確認できるでしょう。

９、管理方法の例

管理方法は、環境に合わせて、構築する必要がありますが、ここでは「在庫流動管理」の一般的な管理方法の概要について説明します。

主な管理項目を列挙します。
＊在庫率＝（(実在庫))/[流動在庫]）
＊インベントリーランク(IR);[流動在庫]の中のインベントリーの位置＝(当該ロットの前にある｛補充在庫｝+((実在庫))/[流動在庫]
＊需要；受注量
＊倉庫在庫数量；((実在庫))

＜在庫率＞

どのSKUが欠品のリスクが高いかを監視するのに在庫率を使います。在庫率は[流動在庫]に対する実在庫数量の比です。在庫が減少してくると数値は低下してきます。ある基準（例えば10%~20%）を設定し、それ以下になったらアラームを出します。表9-1は全体在庫管理表の一例で、在庫率の低い順にソーティングした状態です。欠品状態であれば在庫率はマイナスで表示されます。在庫率の低いSKUは、何らかの回復処置が必要かどうか、詳細情報をクリックして、確認します。

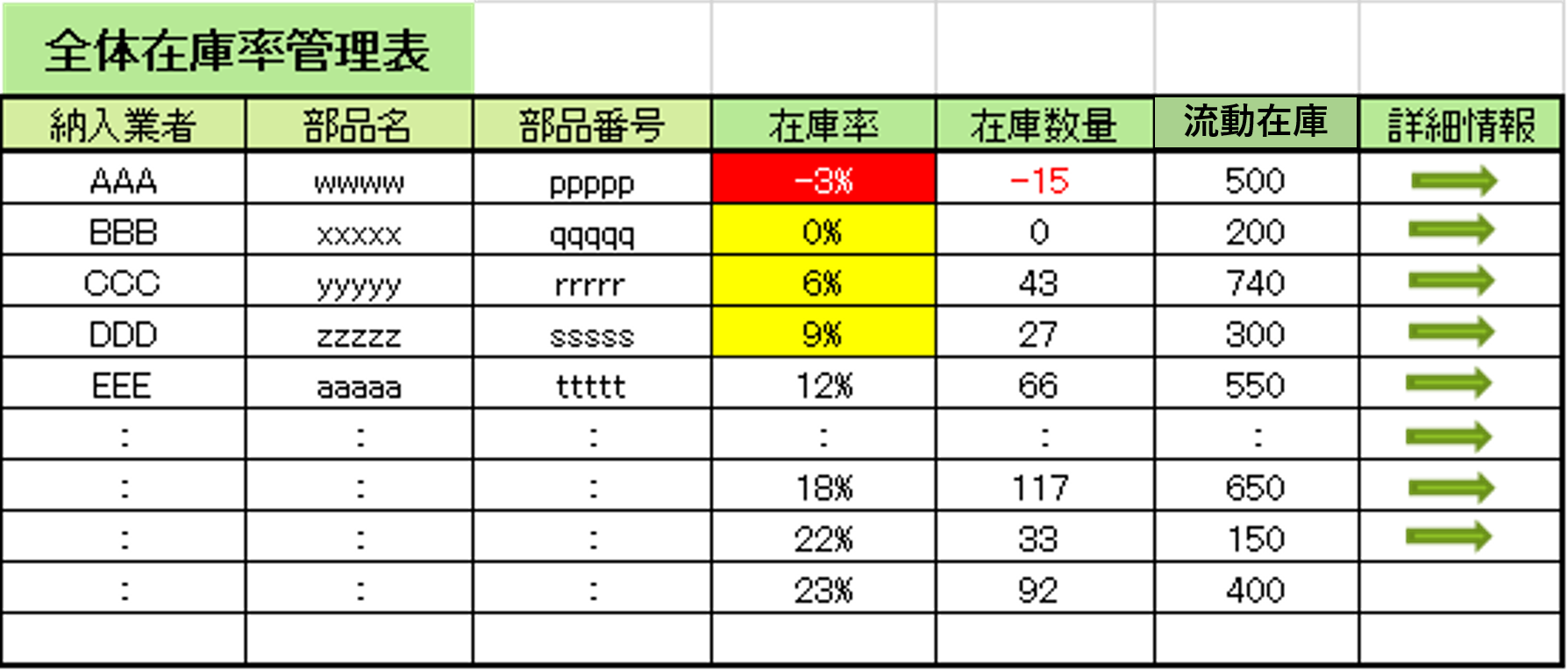
表9-1　在庫管理表の１例

図9-1は全部のSKUの在庫率を視覚化したグラフです。在庫率は、おおむね山形の分布となりますが、補充時間との関係で、山の頂上が50%付近来るとは限りません。通常、どのような分布形状になるかは、環境によって異なりますので、実績データを蓄積して、分析するのが望ましいと思います。在庫率が高すぎる場合は、在庫が過剰である可能性がありますので、こちらも注意が必要です。

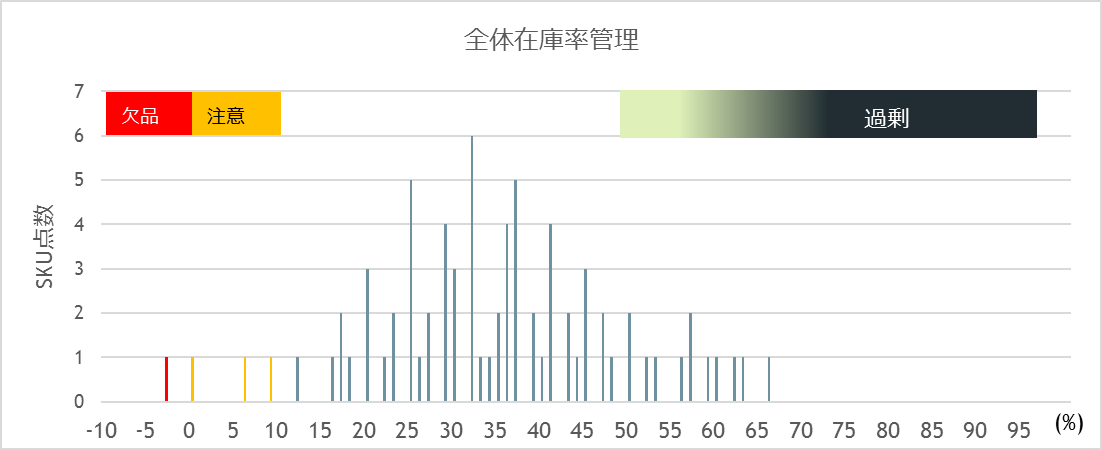
図9-1　在庫管理表のグラフ表示の１例

＜インベントリーランク管理＞

在庫率のアラームが点灯しているSKUの詳細情報をクリックすると、その[流動在庫]の詳細がわかります。表9-2は部品名yyyyyの[流動在庫]の情報です。表中のインベントリーランク（IR）は発注手続き中のロット（発注数量）や発注残が[流動在庫]の中でどこにあるかを示す数値です。

発注残１のインベントリーランク;IRは、43/740=6%、
発注残２のIRは(194+43)/740=32%、
発注残３のIRは(117+194+43)/740=48%、

となります。直近の入庫予定の発注残１のIRと在庫率は同じ値となります。

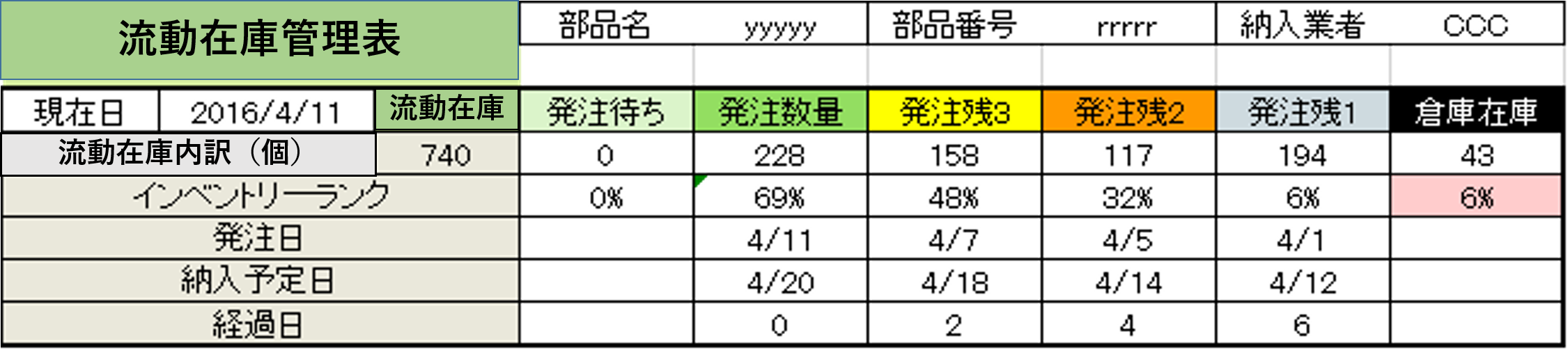
表9-2　部品名yyyyyの[流動在庫]の状態

予定通り発注されているか、約束納期通りに納入されているか等をみて、異常の有無を判断します。図9-2は[流動在庫]とIRの説明図です。

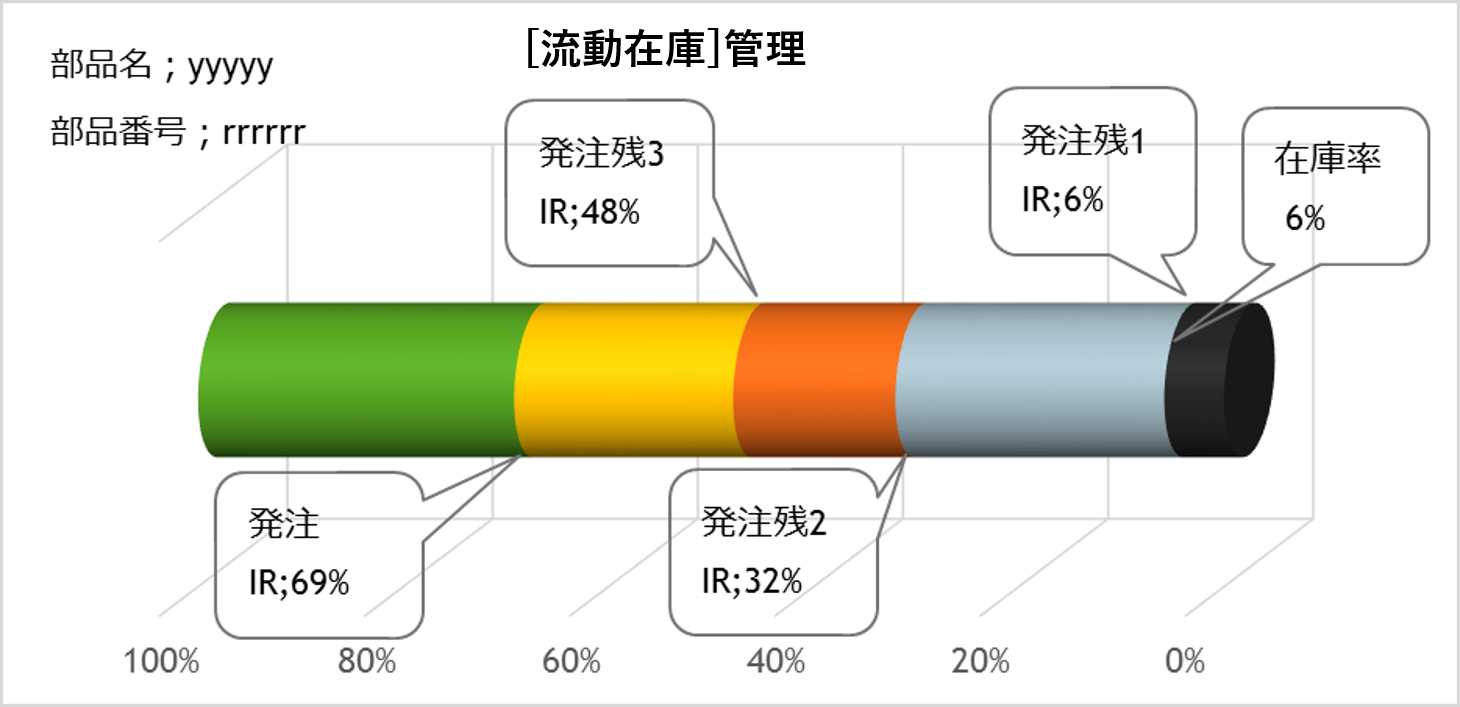
図9-2　[流動在庫]とインベントリ―ランク

図9-3は過去の[流動在庫]の推移を示したものです。一番右側が今日のIRです。どのような経過で今日の状態に至ったか等も参考にします。

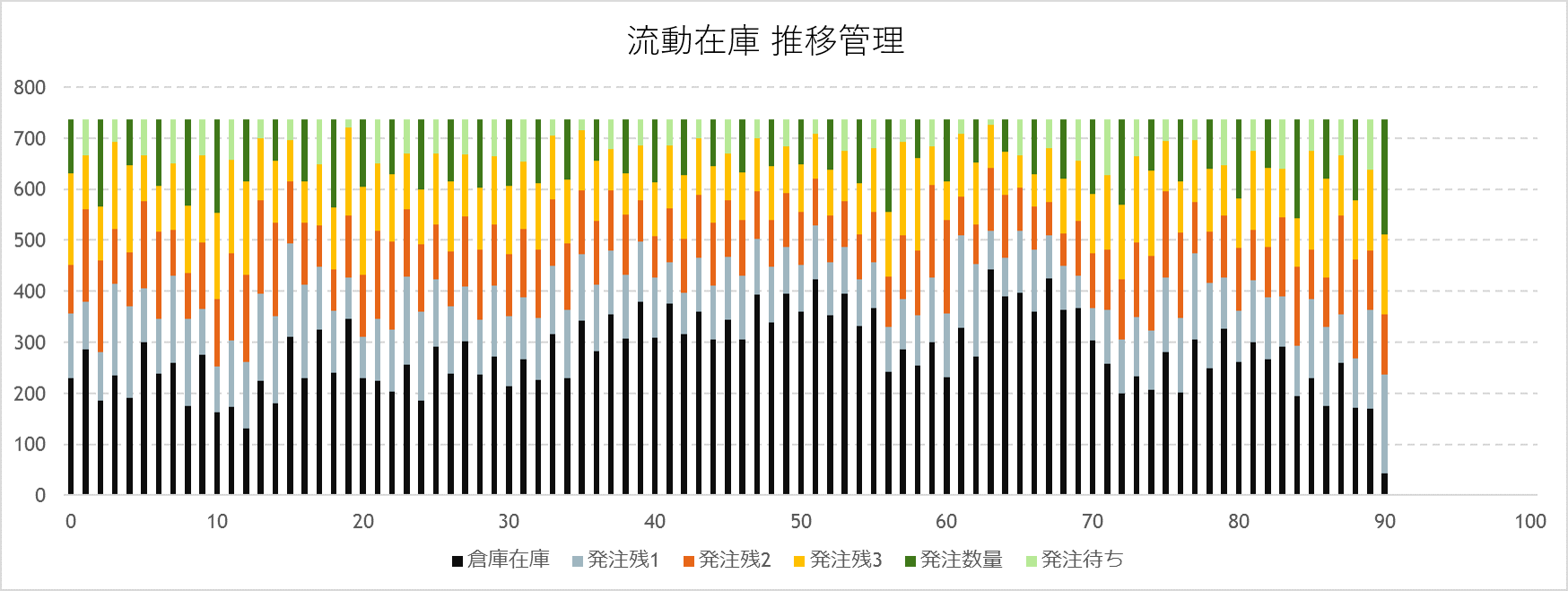
図9-3　[流動在庫]の推移

在庫率が低下する主な要因は二つあります。ひとつは受注数量が増えたこと。もう一つは補充が遅れていることです。この二つを同時に調べる必要があります。図9-4は受注状況のグラフです。破線で示しているのが日毎の受注数量のデータです。実線は5日間の移動平均です。日毎のデータはバラツキが大きく、注文が増えているのか減っているのか判断しにくくなりますが、数日間の移動平均をとると見やすくなります。品質管理でよく使う管理図の原理を利用して、上下の管理限界線を引いて管理するのも一案です。

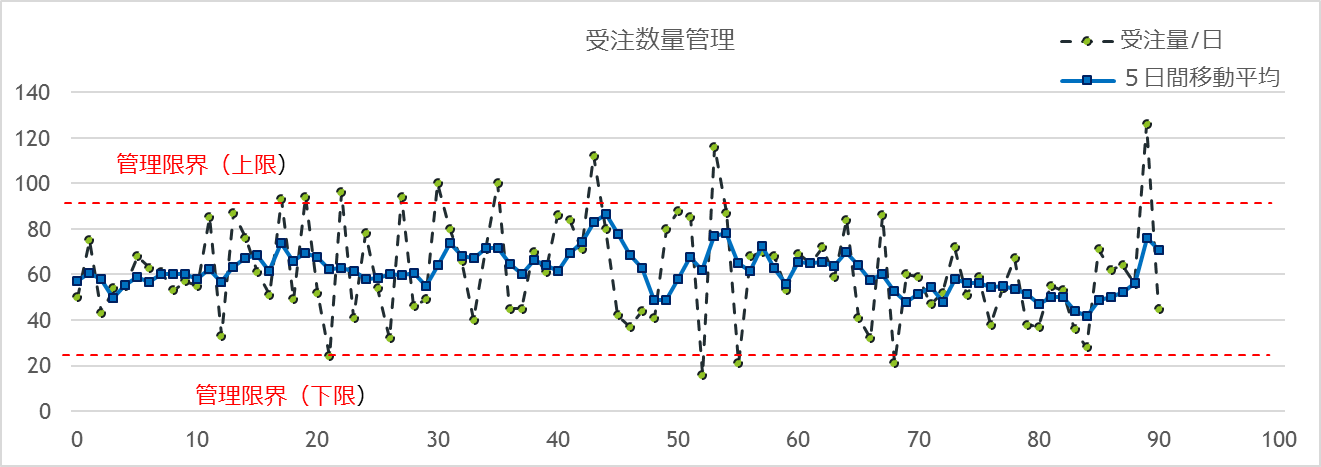
図9-4　受注状況

図9-5は在庫数と在庫率で示した倉庫在庫の推移です。

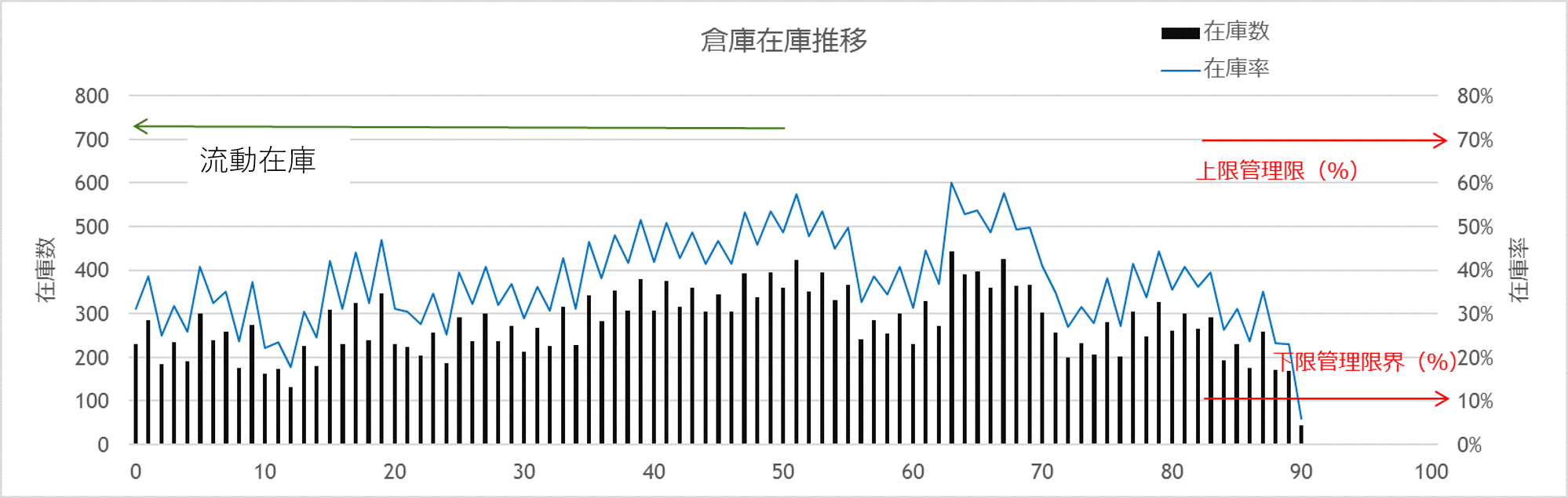
図9-5　倉庫在庫の推移

在庫率低下の二つ目の要因は在庫補充が遅れることです。具体的には、在庫管理側では発注の遅れ、検収・入庫の遅れ等、納入側では理由は様々ありますが、結果的に納入遅れとなることです。納入業者の管理は手薄になりがちになりますが、在庫管理上は重要です。

納期管理の一例として、図9-6に示すように、納期の実績を監視し、納期遵守状況を把握しておきます。突発的な納期遅延の場合もあれば、傾向的に納期遵守率が低下する場合などいろいろあります。中には納期の見直しが必要な場合もあるでしょう。

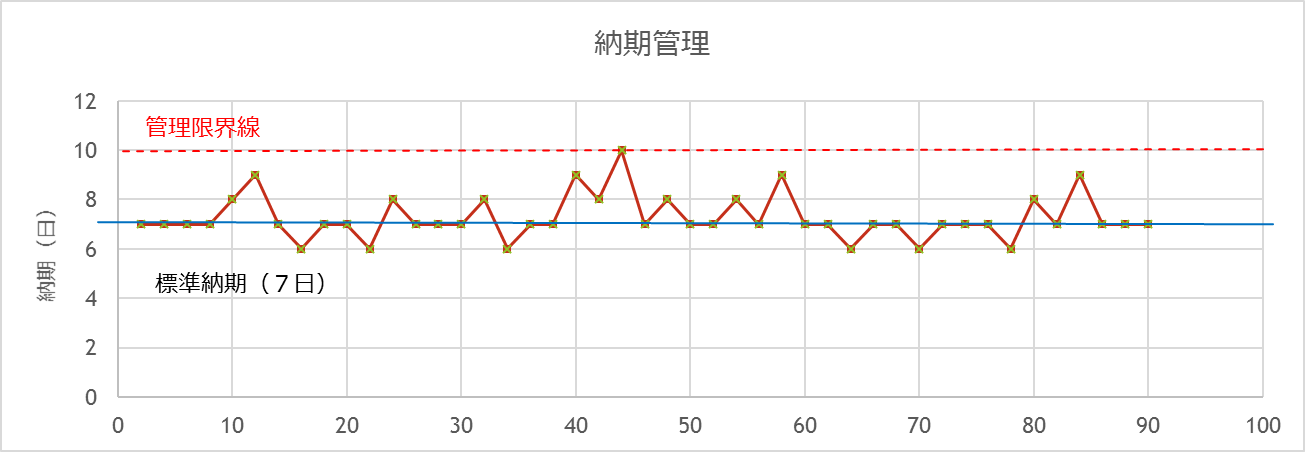
図9-6　納期管理の一例

「在庫流動管理」は、出荷した分だけ発注するという、きわめて簡単な方法ですので、導入も比較的簡単です。試してみてはいかがでしょうか。