生産ラインの特性を学ぶ
1、 生産率、WIP、フロータイム
生産ラインの特性で最も重要なのは生産能力であろう。図1は生産ラインを被加工物(以下、ワーク)が流れ、完成品としてラインアウトする様子を示している。ひとつの製品がラインアウトしてから次の製品がラインアウトするまでの時間間隔(Time Interval;Ti)に着目する。Tiが短ければ短いほど生産能力が高いので、これを使って生産能力を表すことができる。ただ、生産能力を表すには逆数をとった方が分かりやすい。1/Tiを生産率(Throughput;TH)と呼ぶことにする。THの単位は分でも時でも日でも構わない。一般的にtと表現すれば、THのディメンジョンは![]() となる。
となる。

図1 生産ラインからラインアウトするイメージ
工場の生産能力を月産xx台とか、日産yy個ということが多い。THに月をかければ月産数量に、日をかければ日産数量に等しい値となる。従ってTHは生産ラインの能力を表す重要な指標となる。THに任意の時間をかけたものもTHとみなしておく。
![]()
図2 10工程、直列バランスライン
10工程の直列バランスラインを例にして、THの性質およびそれにどのような要素が関係しているか探り出してみる。各工程の処理時間を10分一定で変動はなし、工程間の移動に要する時間はゼロとする。
最初の工程にワークを投入する。処理が終わりP2での処理がはじまるのは10分後。20分後にP2の処理が終わりP3の処理が始まる、、、、という流れでP10が終了するのが100分後。
ここで、100分ごとに投入することにする。つまり最初に投入したワークが完成すると同時に投入する。100分ごと1個投入すると、THは1/100=0.01(1/分)となる。100をかければ100分ごとの完成数となり、100分間のTHは1個となる。
生産ラインンの特性で重要なのが、投入から完成までの時間;フロータイム(Flow Time;FT)と工程仕掛(Work In Process;WIP)である。100分ごとに投入した場合、FTは100分、WIPは1個となる。
今度はワークの投入ペースを50分ごとにしてみる。最初のワークがP5を終了すると同時に2番目のワークを投入する。この時のTHは50分で1個、100分間で2 個となり、WIPは2個。FTは100分ということになる。
投入のペースをさらに上げて20分ごとに投入するとどうなるか。THは20分で1個、100分間で5個。WIPは5個。FTは100分となる。では、10分ごとに投入した場合はどうなるか。 最初のワークがP1での処理が終わると同時に次のワークがP1に投入される。P10からは10分ごとに完成品が出てくるので、THは10分で1個、100分間では10個。WIPはすべての工程にあるので10個。FTはやはり100分で同じ。
THは投入ペースを上げると(投入間隔を狭くすると)それに比例して高くなる。WIPも投入ペースに比例して増える。しかしFTは投入ペースに関係なく、この場合100分で一定である。
これが生産ラインの基本特性中の基本特性。WIPを減らそうとして投入ペースを落とすとTHも低下する。「工程仕掛削減がうまくいったら生産性が落ちた」という話、良く聞くが、背後にこんな特性があることはあまり認識されていない。
さらに投入ペースを上げてみる。9分ごとに1個、投入。P1で1番目のワークの処理が終わらないうちに2番目のワークが投入される。2番目のワークは待つしかない。処理中のワークの処理をやめて、新しく投入されたワークの処理を行うという強引な方法はとらない。処理中のワークの処理が終わるまで待つことにする。2番目のワークは何分待つか。1分待つことになる。2番目のワークが処理中に3番目のワークが投入される。3番目のワークは何分待たなければならないのか? 2番目のワークの処理が終わるのが20分後だが、3番目のワークが投入されるのが18分後なので、2分待つことになる。4番目のワークは3分、5番目のワークは4分、、、と時間経過とともに、待ち時間は長くなる。1番目のワークのFTは100分。2番目のワークのFTは101分。3番目は102分、というようにFTは時間経過とともにどんどん長くなる。
WIPとTHはどうなるか。WIPは、投入工程(P1)の前で待つワークも仕掛なので、時間経過とともに増えてゆく。THはどうなるか。完成は10分に1個(100分間で10個)で、時間が経過しても変わらない。
投入のペースを8分ごとにしたらどうなるか。2番目のワークの待つ時間が2分、3番目のワークの待つ時間は4分、、、となる。FTもその分、長くなる。工程仕掛も時間経過に対して増えるスピードが速くなる。THは100分間で10個で、変わらない。
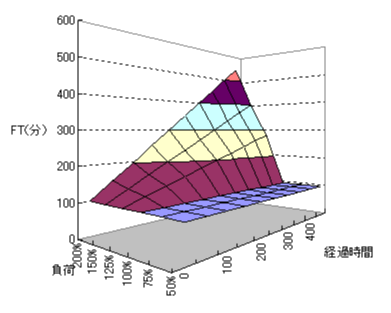
図3 投入負荷vsフロータイム 経過時間での変化
この特性を図で表す。一般的にするために、投入ペースを投入負荷という表現に変えてある。この生産ラインの生産能力は10個/100分なので、投入ペースが10分ごとに1個のとき、投入負荷が100%、20分に1個のときは投入負荷50%、5分に1個のときは200% ということになる。投入負荷と経過時間とFTの関係の一例を図3に示す。
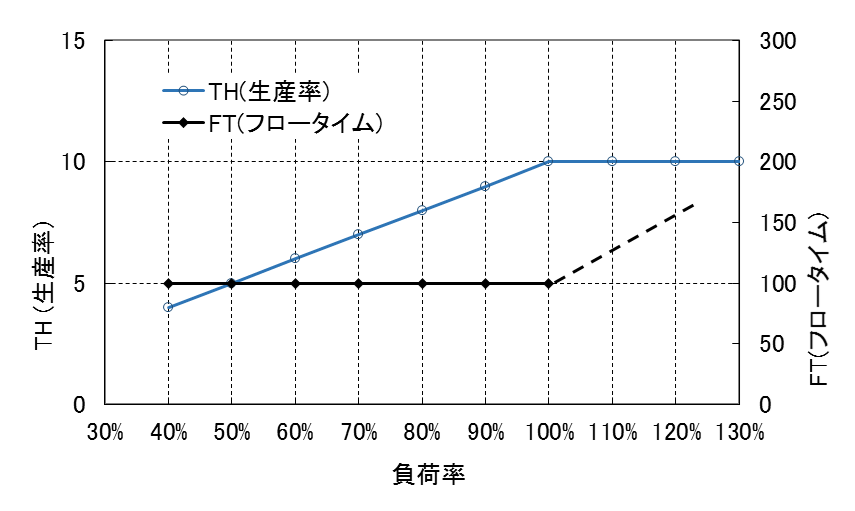
図4 投入負荷に対する生産率とフロータイム
投入負荷に対するTHとFTの関係の一例を図4に示す。FTは負荷率が100%を超えると時間経過とともに長くなるが、時間経過の軸がないので、破線でそのイメージを示しておく。THは負荷率が100%以下では負荷率に比例するが、100%を超えると一定になる。
図5はWIPを基準にFTとTHの関係を示した図である。THはWIPが10個まではWIPに比例するが10個を超えると一定になる。FTはWIPが10個以下では一定であるが、10個を超えるとWIPに比例して長くなる。この図をFITチャート(Flow Time-WIP-Throughput Chart)と呼ぶことにする。FT、WIP、THの3つの基本要素を含み、生産ラインの基本特性を表している。
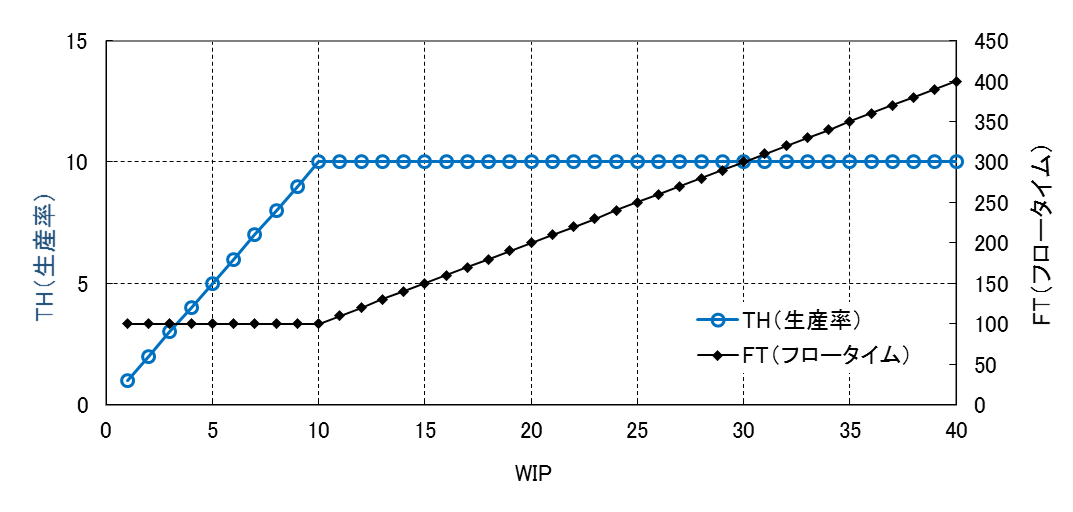
図5 FITチャートの一例
図6はFT、WIP、THを流動数曲線で表したものである。FITチャートと比較してみると参考になる。
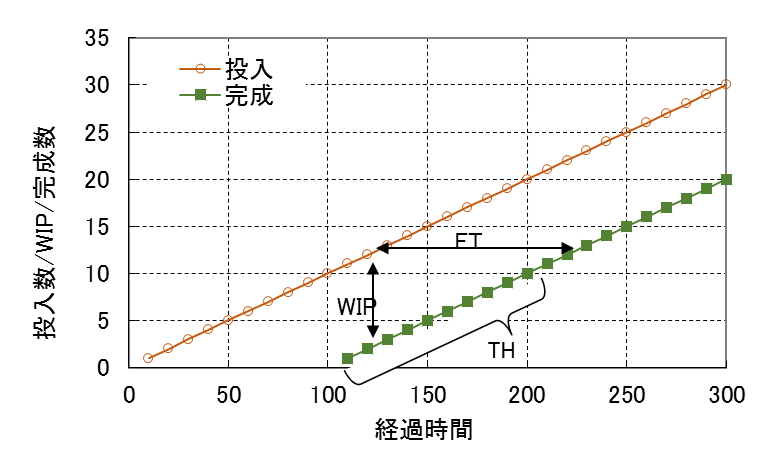
図6 流動数曲線でFT、WIP、THの関係を表す
2、FITチャートでみる生産ラインの特性
FITチャートはTH(生産率)、WIP(工程仕掛)、FT(フロータイム)の関係を示している。この関係をもう少し詳しくみてみる。
THはWIPが10個まではWIPに比例するが10個を超えると一定になる。FTはWIPが10個以下では一定であるが、10個を超えるとWIPに比例して長くなる。TH、WIP、FTの関係は「リトルの法則(Little's Law)」として知られ、式で表せば、
WIP=TH x FT -------------式1
となるが、THとFTが屈曲しているWIPがどこになるかを知る必要がある。そのWIPをC-WIP(Critical WIP)、工程の中で一番能力の低い工程(ボトルネック工程)の処理時間をTmaxとすれば、(バランスラインの時はどれか1工程の処理時間)
C-WIP=FT/Tmax -------式2
で求められる。
WIP ≦ C-WIPのとき、
FT一定 ------------------式3
TH=WIP/FT ----------式4
WIP ≧C-WIPのとき、
FT=WIPxTmax ---------式5
TH=1/Tmax -------------式6
WIPがC-WIP以上増えてもTHは増加しない。WIPがC-WIP以下ではFTが最短となるが、WIPに比例してTHは低下する。WIPがC-WIPの時、THが最大でFTが最短となる。THは生産ラインの生産能力を、FTは需要への追従能力を示していると考えるとわかりやすい。生産ラインの条件を変えてFITチャートがどのように変わるのかをみて、10工程直列バランスライン(1工程処理時間10分)を事例にして、生産ラインの特性の理解を深めてゆく。
<待ち時間がある場合>
工程間の運搬待ちや処理待ちなど、待ち時間があるのが普通である。待ち時間がある場合、FITチャートはどうなるのか。各工程終了後に5分の待ち時間あるとする(最終工程も5分待って完成)。FTは、処理時間と待ち時間の合計で、
FT=10(工程) x 10(分) + 10(工程) x 5(分) = 150 (分)
となる。Tmaxはバランスラインで10(分)なので、C-WIPは、
C-WIP=FT/Tmax = 150(分)/10(分) = 15 (個)
WIP ≦ C-WIPのとき、
FTは150(分)で一定
TH=(WIP/FT) x 100(分) = 0.667 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
これをFITチャートで表すと図7のようになる。待ち時間が加わったことにより、C-WIPが10個から15個に増える。WIP≧C-WIPでのTHとFTは変わらないが、WIP≦C-WIPではTHが低下しFTが長くなる。待ち時間が長くなればなるほどWIP≦C-WIPの領域が広くなり、生産ラインの能力は低くなる。
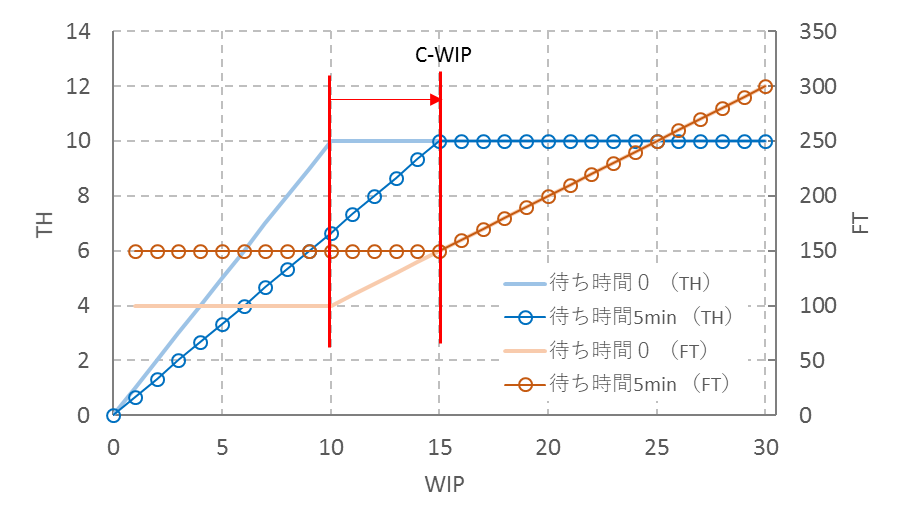
図7 待ち時間がある場合のFITチャート
<1工程の処理時間が長くなった場合>
10工程直列バランスラインで各工程の処理時間が10分より長くなったらどうなるか。10分が15分になった場合と20分になった場合についてみてみる。
◆ 15分の場合
FT=10(工程) x 15(分) = 150 (分)
となる。Tmaxはバランスラインで15(分)なので、C-WIPは、
C-WIP=FT/Tmax = 150(分)/15(分) = 10 (個)
WIP ≦ C-WIPのとき、
FTは150(分)で一定
TH=(WIP/FT) x 100(分) = 0.667 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 15 x WIP (分)
TH=(1/Tmax) x 100(分) = 6.67 (個/100分)
◆ 20分の場合
FT=10(工程) x 20(分) = 200 (分)
となる。Tmaxはバランスラインで20(分)なので、C-WIPは、
C-WIP=FT/Tmax = 200(分)/20(分) = 10 (個)
WIP ≦ C-WIPのとき、
FTは200(分)で一定
TH=(WIP/FT) x 100(分) = 0.5 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 20 x WIP (分)
TH=(1/Tmax) x 100(分) = 5 (個/100分)
これをFITチャートで表すと図8のようになる。各工程の処理時間が長くなってもC-WIPは変わらない。但し、処理時間が長くなるに従いTHは全体的に低下し、FTは全体的に長くなる。
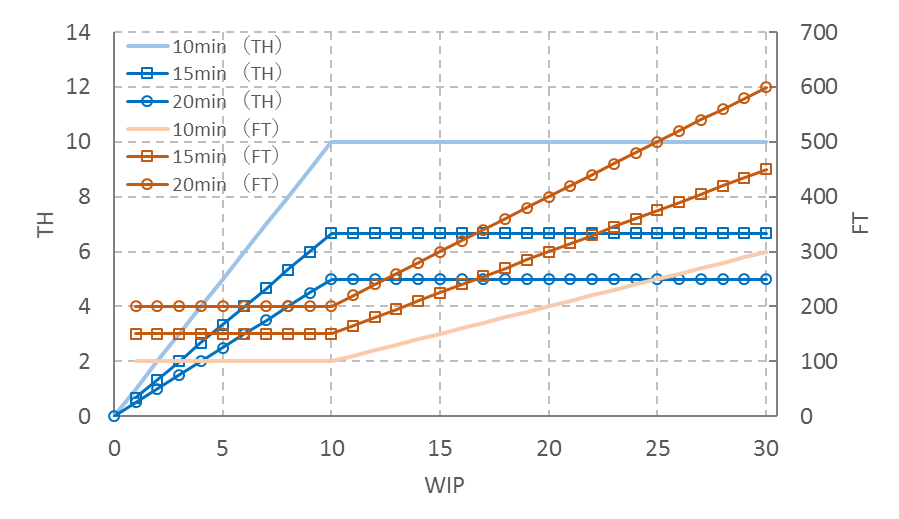
図8 工程の処理時間が長くなった場合
<工程数の変化>
各工程の処理時間は10分のままで、工程数を増やした場合はどうか。工程数を5と15で検討してみる。
◆ 5工程
FT=5(工程) x 10(分) = 50 (分)
となる。Tmaxはバランスラインで10(分)なので、C-WIPは、
C-WIP=FT/Tmax = 50(分)/10(分) = 5 (個)
WIP ≦ C-WIPのとき、
FTは50(分)で一定
TH=(WIP/FT) x 100(分) = 2 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 5 (個/100分)
◆ 15工程
FT=15(工程) x 10(分) = 150 (分)
となる。Tmaxはバランスラインで10(分)なので、C-WIPは、
C-WIP=FT/Tmax = 150(分)/10(分) = 15 (個)
WIP ≦ C-WIPのとき、
FTは150(分)で一定
TH=(WIP/FT) x 100(分) = 0.667x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
FITチャートで表すと図9のようになる。
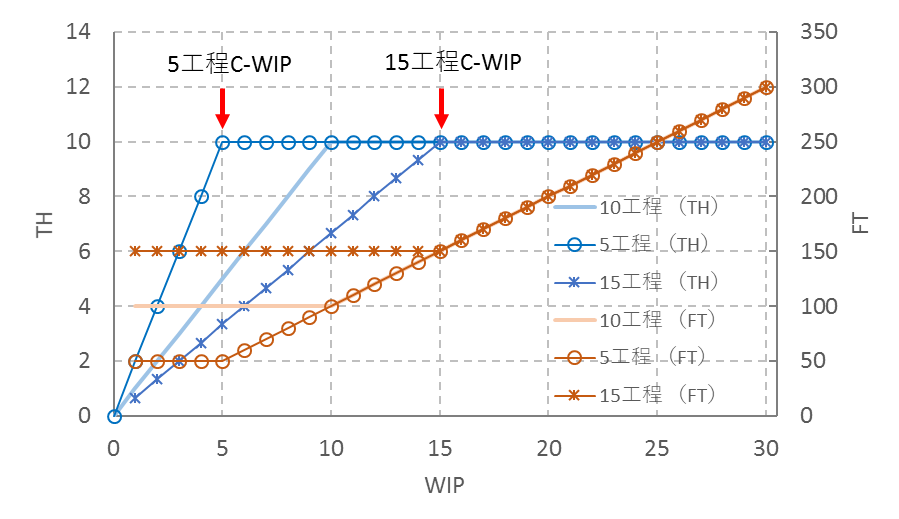
図9 工程数が5と15の時のFITチャート
5工程ではC-WIPが5個、15工程では15個になる。C-WIP以上の領域ではTHもFTもまったく同じであるが、C-WIP以下では図9に示すように変化する。
<FTはそのままで、工程数と処理時間を変える>
FTは100分のままで、工程数と処理時間を変えてみる。
◆ 20工程、処理時間5分
FT=20(工程) x 5(分) = 100 (分)
となる。Tmaxはバランスラインで5(分)なので、C-WIPは、
C-WIP=FT/Tmax = 100(分)/5(分) = 20 (個)
WIP ≦ C-WIPのとき、
FTは100(分)で一定
TH=(WIP/FT) x 100(分) = 1 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 5 x WIP (分)
TH=(1/Tmax) x 100(分) = 20 (個/100分)
図10はFITチャートである。10工程・10分と比べ、WIPが10(個)を超える領域でTHが高くなりFTが短くなる。
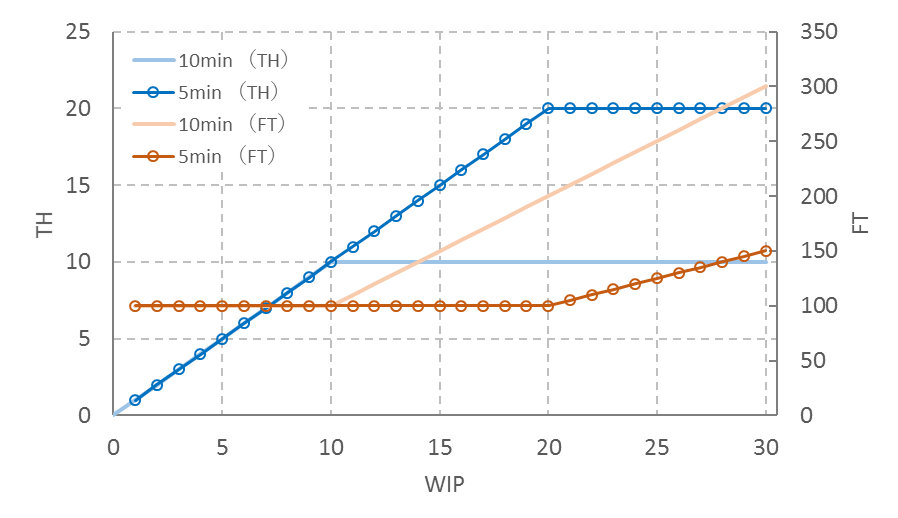
図10 20工程、処理時間5分でのFITチャート
◆ 5工程、処理時間20分
FT=5 (工程) x 20(分) = 100 (分)
となる。Tmaxはバランスラインで20(分)なので、C-WIPは、
C-WIP=FT/Tmax = 100(分)/20(分) = 5 (個)
WIP ≦ C-WIPのとき、
FTは100(分)で一定
TH=(WIP/FT) x 100(分) = 1 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 20 x WIP (分)
TH=(1/Tmax) x 100(分) = 5 (個/100分)
図11はFITチャートである。10工程・10分と比べ、WIPが5(個)を超える領域でTHが低下しFTが長くなる。
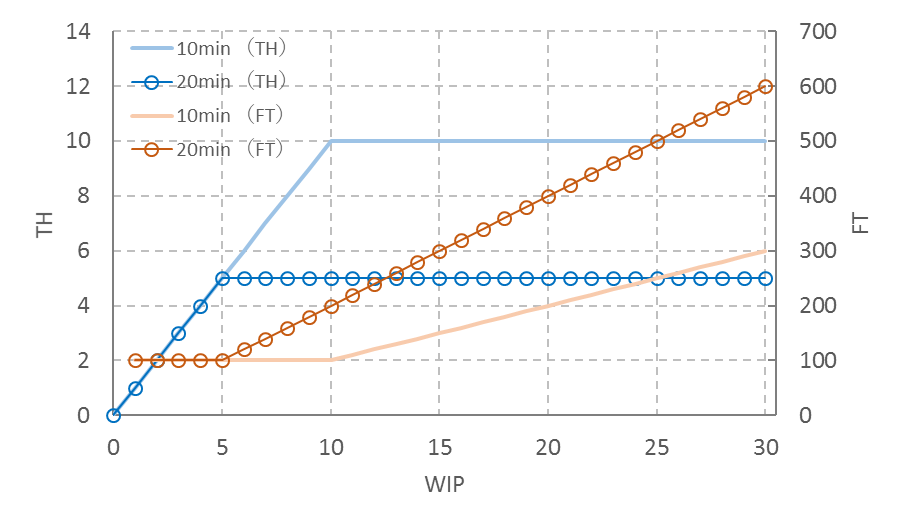
図11 5工程、処理時間20分でのFITチャート
<ボトルネック工程がある場合>
図2の10工程直列バランスラインのP5の処理時間は10分のままで、その他の工程の処理時間を6分に短縮した場合、P5はボトルネックとなる。FITチャートはどうなるか。C-WIPを求めてみる。
FT=10(分)+9x6(分)=64(分)
となる。Tmaxは10(分)なので、C-WIPは、
C-WIP=FT/Tmax = 64(分)/10(分) = 6.4 (個)
WIP ≦ C-WIPのとき、
FTは64(分)で一定
TH=(WIP/FT) x 100(分) = 1.56 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
C-WIPが10個から6.4個に移動し、C-WIP以上のTHは10(個/100分)となる。FITチャートで表すと図12のようになる。C-WIPは、端数となるため丸みを帯びる。
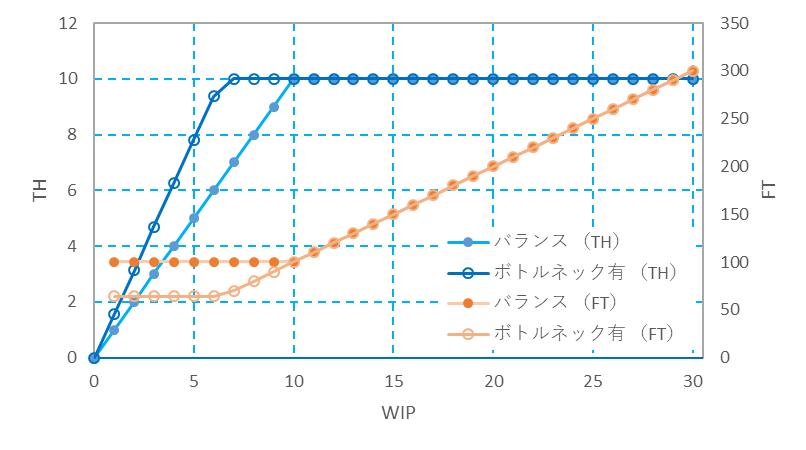
図12 ボトルネックがある場合のFITチャートの一例
3、バッチ処理がある場合
午前に1回、午後に1回運搬するとか、段取り時間を節約するためにまとめて処理するといったまとめ作業は頻繁に行われている。まとめ作業を時間で捉える場合を時間バッチ、数量で捉える場合を数量バッチと呼んでおく。このようなバッチ処理によって待ち時間が発生するが、それがどのように生産ラインの特性に影響するかを検討する。
<バランスラインで、時間バッチがひとつ>
工程内に時間バッチがある場合、FT(フロータイム)とTH(生産率)にどのような影響があるのかを調べてみる。10工程直列バランスラインで各工程の処理時間は10分固定、P4からP5へ移動するとき、50分ごとに搬送する場合を例にして、その動きをみてみる。
FTは、処理時間と時間バッチを合計して、
FT=10(分) x 10+50(分)=150(分)
となる。Tmaxはバランスラインなので10(分)、C-WIPは、
C-WIP=FT/Tmax = 150(分)/10(分) = 15 (個)
WIP ≦ C-WIPのとき、
FTは150(分)で一定
TH=(WIP/FT) x 100(分) = 0.667 x WIP (個/100分)
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
時間バッチがある場合とない場合のWIPに対するFTとTHをFITチャートで図13に示す。
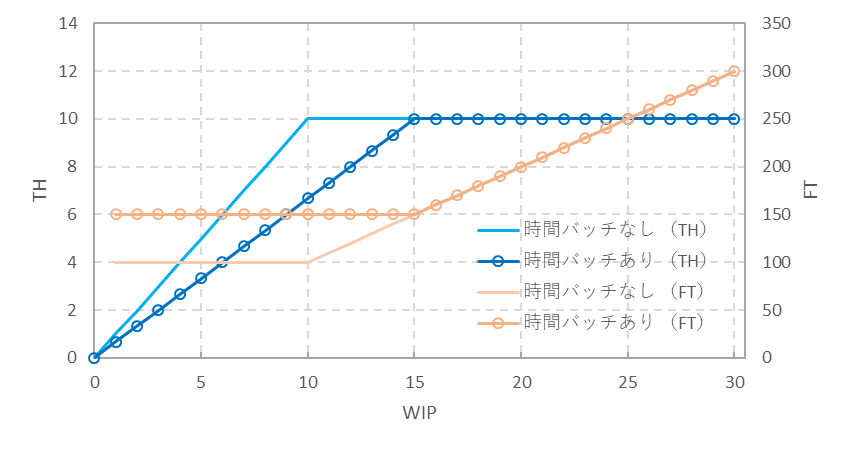
図13 1か所で時間バッチがある場合のTHとFT
<バランスラインで、時間バッチが複数>
時間バッチが複数個所ある場合、FTとTHはどうなるか。P4とP5の間に50分、P7とP8の間に80分の時間バッチがある場合について検討してみる。時間バッチが2か所あると、FTとTHは単純な直線ではなく、複雑な動きをみせる。数式ではわかりづらいので、シミュレーションを行う。シミュレーションソフトは「SIMUL8」を使用。図14にTHのシミュレーション結果を示す。黒の一点鎖線が平均、実線が最高、破線が最低である。例えばWIPが15ではTHの最低が5.6、最高が10で平均は7.2である。
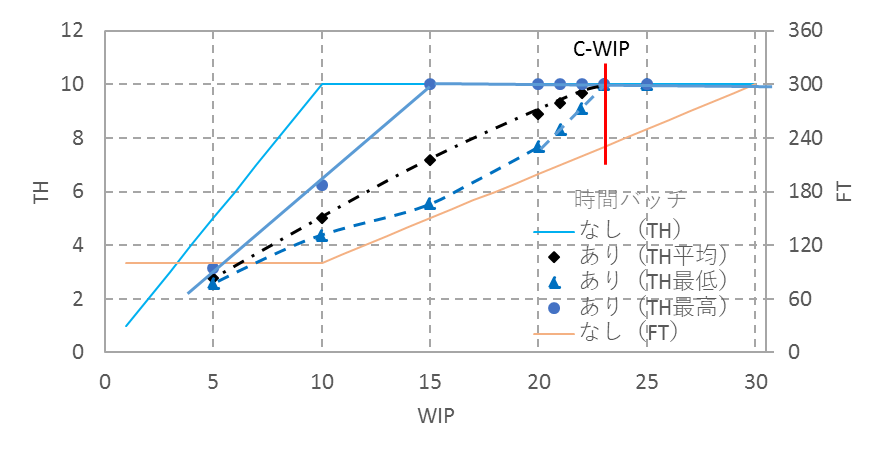
図14 時間バッチが2か所ある場合のTHのシミュレーション結果
図15にWIPが15で、時間経過とともにTHがどのように変化するかの1例を示す。
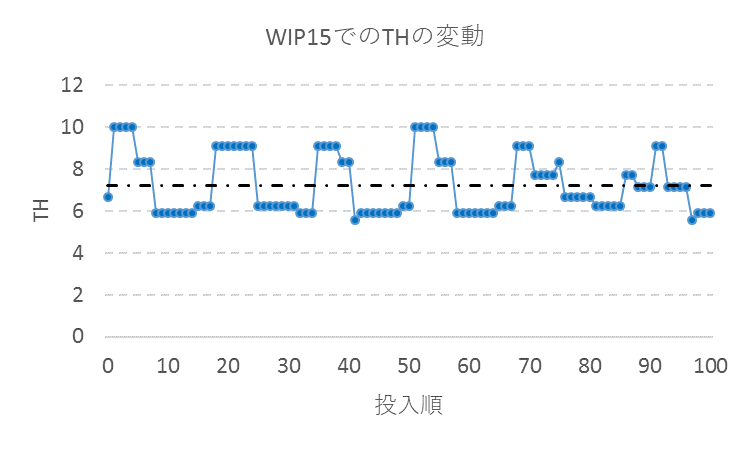
図15 THの変動の1例
次に、FTのシミュレーション結果をみてみる。図16に結果の1例を示す。最短が160分、最長が230分である。
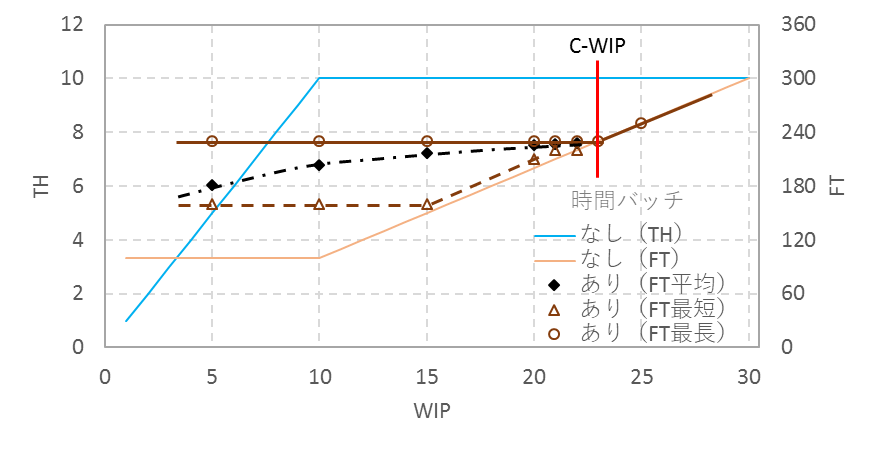
図16 時間バッチが2か所ある場合のFTのシミュレーション結果
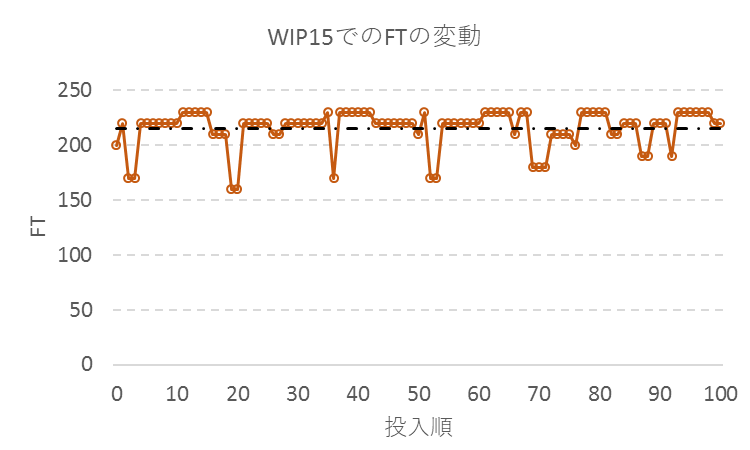
図17 FTの変動の1例
これまで使ってきた式の計算結果とシミュレーション結果を比較してみる。
FTは、処理時間と時間バッチを合計して、
FT=10(分) x 10+50(分)+80(分)=230(分)
となるが、これはシミュレーションのFTの最長と一致する。
Tmaxはバランスラインなので10分、C-WIPは、
C-WIP=FT/Tmax = 230(分)/10(分) = 23 (個)
シミュレーションでのTHもFTも、WIPが23個で屈曲している。
WIP ≦ C-WIPのとき、
シミュレーションのFTの最長値と一致するが、最短値の算出式はない。
TH=(WIP/FT) x 100(分) = 0.435 x WIP (個/100分) は、両者一致する。
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
となり、FTもTHも両者一致する。
まとめると、式1~式6は、
① C-WIPの算出に適用できる(式1、式2)
② WIP ≦ C-WIPの領域では、(式3)FTは最長値を示す。(式4)はTHの平均値を示す。
③ WIP ≧C-WIPの領域で(式5、式6)の適用ができる。
<ボトルネックラインで、時間バッチがある場合>
P7の処理時間が10分、他の工程の処理時間が6分のボトルネックラインで、P5前に時間バッチがあるとどうなるか。時間バッチ 100分の場合について検討してみる。これも、先ず、シミュレーションで確認してみる。シミュレーション結果の一例を図18に示す。
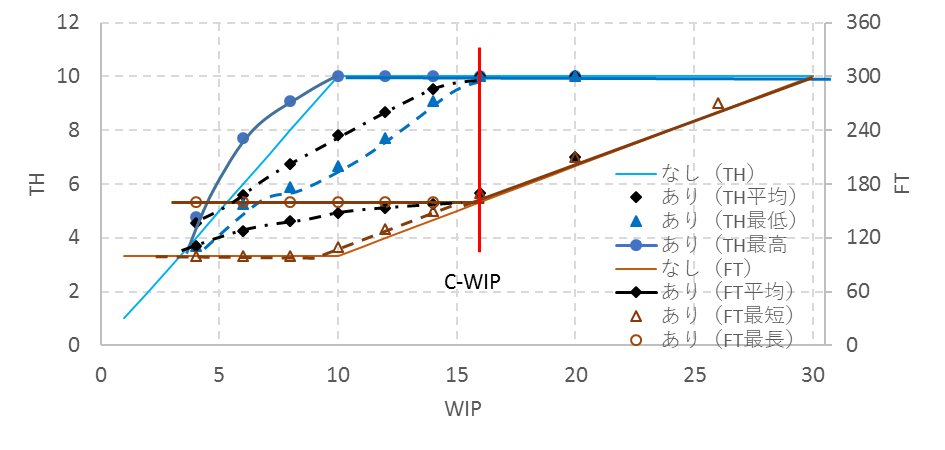
図18 ボトルネックラインで時間バッチがある場合のTHとFT
図19はWIPが10でのTHの変化、図20はFTの変化の一例である。
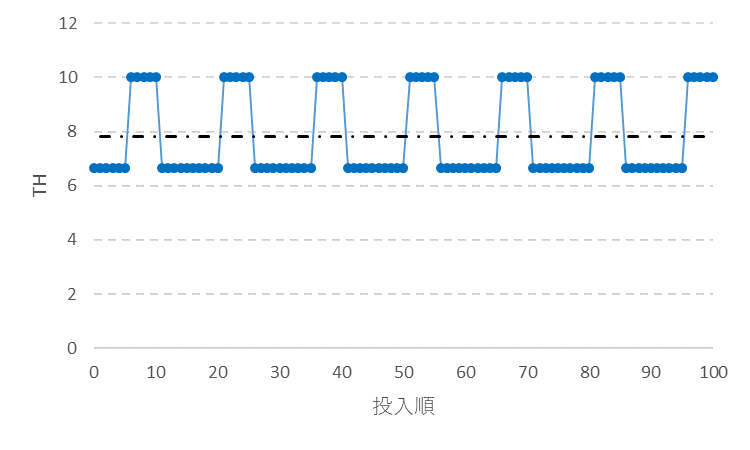
図19 WIP10でのTHの変化
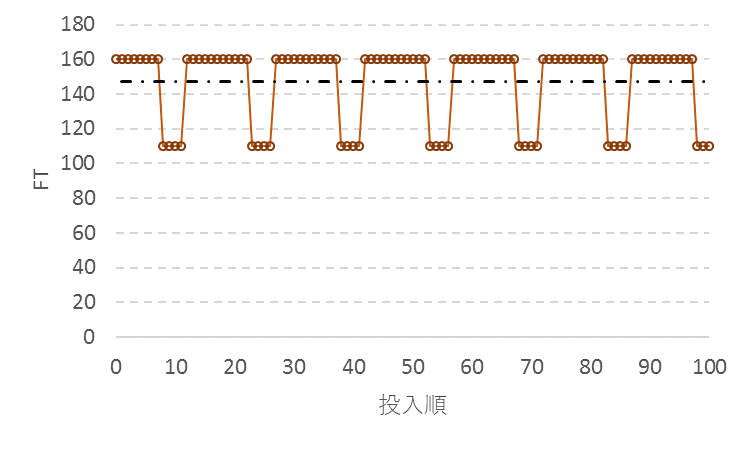
図20 WIP10でのFTの変化
数式と比べてみる。
FTは、処理時間と時間バッチを合計して、
FT=10(分)+6(分) x9+100(分)=164(分)
となる。Tmaxはボトルネックラインで10(分)、C-WIPは、
C-WIP=FT/Tmax = 164(分)/10(分) = 16.4 (個)
C-WIPはシミュレーションと一致する。
WIP ≦ C-WIPのとき、
FTは164(分)で一定
TH=(WIP/FT) x 100(分) = 0.61 x WIP (個/100分)
FTはシミュレーションの最長値と一致する。THは平均値と一致する。
WIP ≧C-WIPのとき、
FT=WIPxTmax = 10 x WIP (分)
TH=(1/Tmax) x 100(分) = 10 (個/100分)
FTもTHも計算値とシミュレーションは一致する。
<数量バッチがある場合>
炉での熱処理や段取り時間が長い場合のまとめづくりなど、数量でバッチを形成する場合がある。このような数量バッチがある場合、THとFTがどうなるか調べてみる。P9が処理時間10分、他は6分のボトルネックラインで、P6で4個、P9で7個のバッチ処理を行うことにする。シミュレーション結果の1例を図21に示す。
C-WIPの位置が16個付近にある。バッチ処理によるWIPの増加は、4-1=3(個)と7-1=6(個)の合計9個である。それ以外のFTは6x9+10=64(分)で、C-WIPはC-WIP=64/10+9=15.4(個)となり、ほぼシミュレーションと一致する。
WIP ≧C-WIPの領域では、計算式とシミュレーションは一致するが、WIP ≦ C-WIPの領域では一致しない。
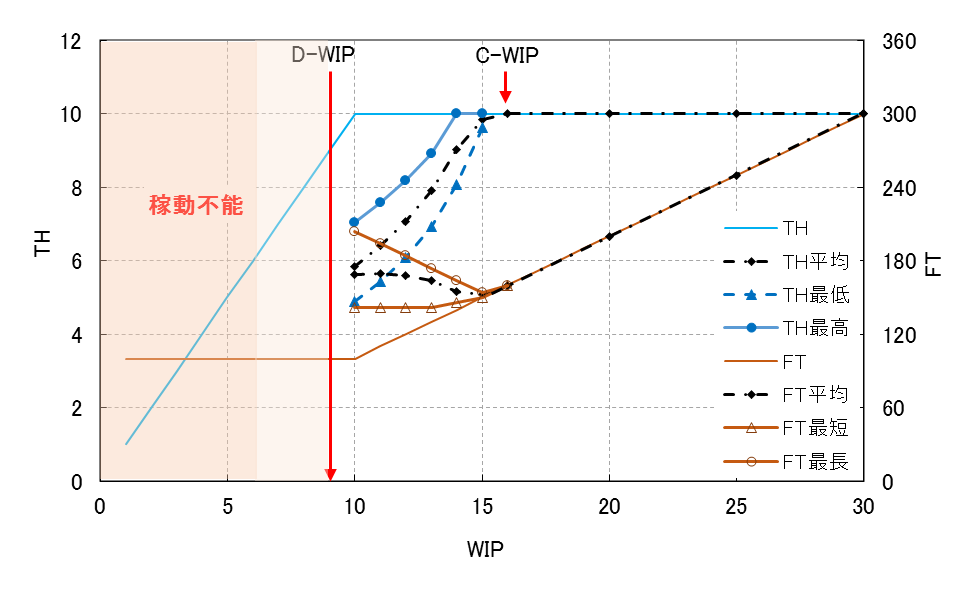
図21 ボトルネックラインで数量バッチがある場合のTHとFT
時間バッチの場合と異なるのは、図21のピンクで示した部分である。7個のバッチ処理がある場合、WIPが6個以下ではバッチ処理が行われず、流れが停止する。またWIPが9個の時、4個のバッチ処理で3個、7個のバッチ処理で6個の状態となれば、流れは止まる。前者は100%止まるが、後者はある確率で止まる。バッチ処理の場所が多ければ止まる確率は低くなることが予想されるが、止まるリスクはある。工程の流れが止まる可能性のあるWIPをD-WIP (Deadlock WIP) と呼んでおく。
4、投入時間間隔、処理時間が変動する場合
生産ラインの条件を変えて、FT、WIP、THがどのようになるのかをみてきた。条件はすべて定数を用いたが、時間バッチが複数ある場合、時間バッチは1つでもボトルネックラインの場合、数量バッチがある場合は、投入時間間隔、処理時間が一定でもFTとTHはある範囲内でばらつく。実際の生産ラインでは、処理時間、待ち時間など一定であることはほとんどない。そのような場合、FTとTHはどのようにばらつくのか調べてみる。
<ランダムに変動する場合>
検討するモデルは、これまでと同じ10工程直列ラインとする。変動条件は最もランダム性の高い指数分布を用いる。次の条件でシミュレーションを行う。
投入時間間隔;平均10分、指数分布(変動係数は1)
各工程の処理時間;平均10分、指数分布
WIP;5、10、~35、40個
データはWIPを固定して、立ち上がりを除いた安定状態のTHとFTを観察する。THのシミュレーション結果の1例を図22に示す。THの最高と最低および平均、WIP 40個でのTHの分布を示している。直線は変動がまったくない場合のTHである。
THは、その集計方法(集計期間や個数)によって値が異なる。期間が長く、個数が多ければバラツキの範囲は狭くなるが、特徴はつかみにくくなる。ここでは、(10個)÷(10個完成する時間) で計算し、移動平均をとってTHを算出している。
THの最高値は変動のないときのそれを超えるが、平均値は超えることはない。これは、変動が加わるとTHは低下することを意味する。THの分布は、このシミュレーション結果では、指数分布を用いたためか、非対称な山形となっているが、実用的な範囲では正規分布に近似できるのではないかと思われる。もうひとつ気が付くことは、WIPがいくら多くなっても、THの屈曲点(C-WIP)がないことである。
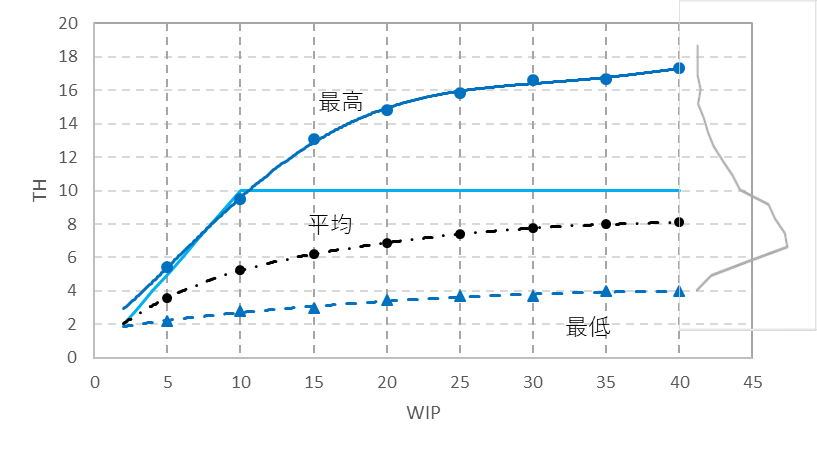
図22 指数分布による変動がある場合のTH
次に、FTをみてみる。シミュレーション結果を図23に示す。変動がないときのFTと比べ、変動が加わると、FTの平均値は長くなる。WIPに比例する性質は保たれているが、こちらも屈曲点はなくなっている。
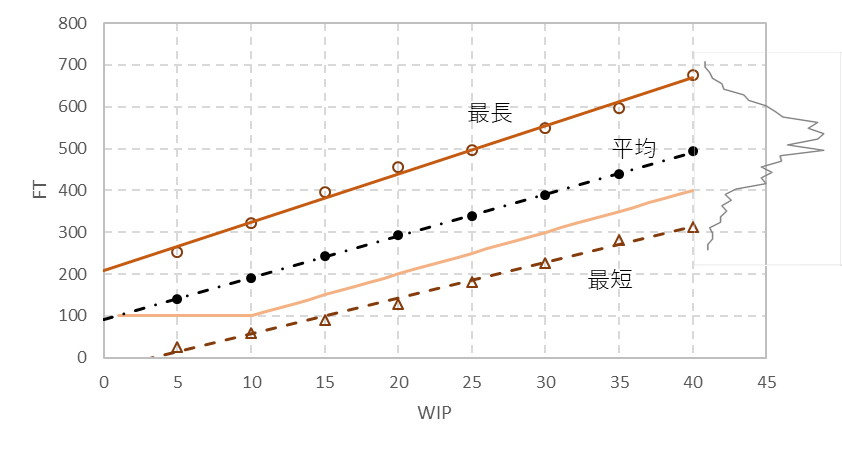
図23 指数分布による変動がある場合のFT
変動の程度によって、どの程度変わるか、処理時間を変動係数0.25の正規分布で変動させたときのシミュレーションした結果を図24と図25に示す。THとFTのばらつきの範囲が狭まることが分かる。
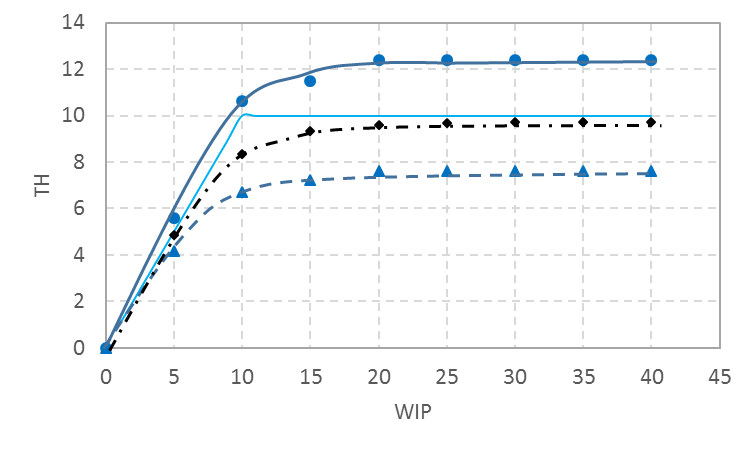
図24 正規分布(変動係数0.25)による変動がある場合のTH
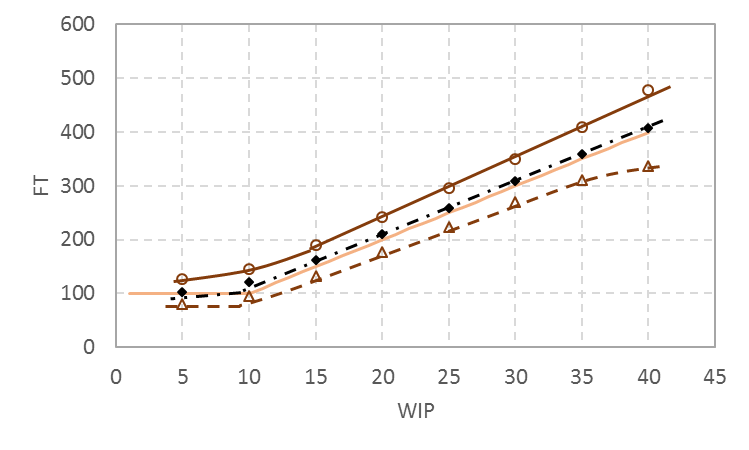
図25 正規分布(変動係数0.25)による変動がある場合のFT
<フロータイム(FT)の跳ね上がり>
図22のTHの平均(一点鎖線)に対するFTの関係を書き直してみると図26のようになる。直線は変動のないとき、点はシミュレーション結果、曲線は計算値である。(投入時間間隔、処理時間は指数分布)
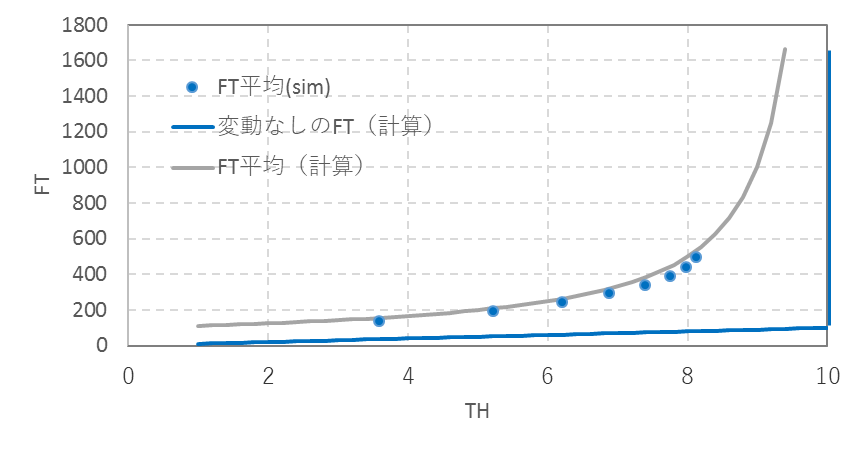
図26 THとFTの関係
THは生産能力に対する生産数量とみることができる。設備の稼働状態でみれば稼働率、負荷でみれば負荷率とみることもできる。稼働率をρとすれば、FTは次のようになる。
FT=10(工程) x 10(分) + 10(工程) x 10(分)xρ/(1-ρ)
ρ=TH/10なので、
FT=100 x {1+ TH/(1-TH)}
1項目は処理時間、2項目は待ち時間である。図26に示すように、稼働率が80%付近から急激にFTが長くなる。これを「フロータイムの跳ね上り」と呼んでおく。
補足)投入時間間隔が指数分布、処理時間も指数分布、処理工程数1ヶ所の場合(待ち行列理論ではM/M/1モデル)の平均待ち時間は;
平均処理時間×ρ/(1-ρ)
で求められる
<稼働率に対するFTと完成数の関係>
「フロータイムの跳ね上り」は生産管理、特に納期管理ではきわめて重要である。稼働率に対して、あるFT以内に完成する数量がどのようになるかをシミュレーションしてみる。これまでと同じ10工程直列バランスラインで、投入時間間隔は指数分布(変動係数1)、処理時間はk=2のアーラン分布(変動係数0.7)で変動するという条件で、FTが100分以内、300分以内、400分以内、600分以内に完成する個数をカウントする。データ収集時間は10,000分とした。
シミュレーション結果の1例を図27に示す。FTが400分、600分では、稼働率が高くなるに従って完成数も増えてゆくが、80%を超えると逆に減少する。これは、FTが急激に長くなり、時間以内に完成しなくなるものが多くなるためである。FT200分以内の条件では、稼働率50%を超えると、完成数が減少する。稼働率が高くなれば完成数も多くなるとは言えないのである。
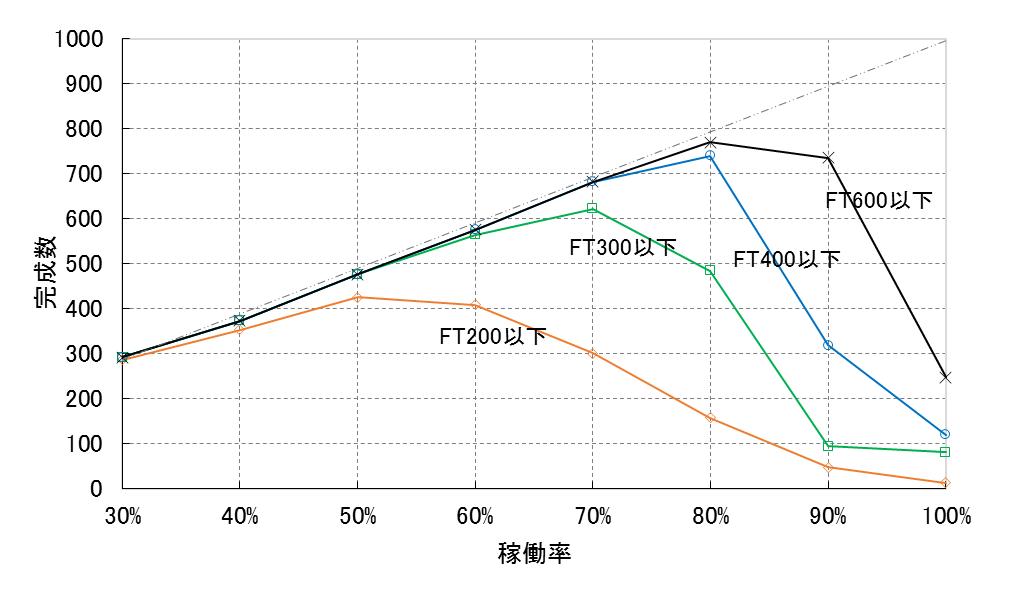
図27 稼働率に対するFT以内の完成数
現行の生産計画を基準とした生産管理がうまく機能しない大きな要因のひとつがこの「フロータイムの跳ね上り」を考慮していないためではないか、と思われる。稼働率は高い方が良いとされ、80%よりは90%を、いや、95%を目指そうとなる。そうするとフロータイムが急激に長くなり、完成が遅れ、納期に追われながら悪戦苦闘することになる。
日程計画に空白があるとみっともない。隙間なく、びっしりと仕事を入れるのが計画担当の性。「フロータイムの跳ね上り」に対し、何らかの手を打つことは、生産管理上の必須条件であることに留意しておかなければならない。
5、フロータイムの跳ね上りを抑える
FITチャートで生産ラインの特性をみてきた。処理時間に変動がない場合、WIPがC-WIPより多いとTHが一定となり、FTはWIPに比例して長くなる。THが最高でFTが最短のポイントはC-WIPである。処理時間が変動する場合その変動幅が大きくなるに従いTHの変動幅も広くなる。THの平均は図22、図24に示すように、WIPの増加とともにTHの最高点に漸近する。FTはWIPに比例する特性はそのままだが、その変動幅も広がり、平均も長くなる。またC-WIPの位置が不明確になる。
THを基準にFTがどのようになるかをみると、「フロータイムの跳ね上り」という現象がみえてくる。少し脱線するかもしれないが、この「フロータイムの跳ね上り」をどのように抑えているのか。トヨタ生産方式では平準化とタクトタイムでの同期生産、無駄の排除等により、変動を小さくすることを目指している。そしてWIPを C-WIP+α に制限し生産ラインの安定を図っている。TOCが提唱するS-DBRではタイムバッファーを設定し、投入制限し、WIPの必要以上の増加を抑制している。CONWIP(Constant WIP)という工程内のWIPを一定に保つ生産方式もある。
従前から、WIP増による弊害は認識されていた。しかし、製造業全体を見回せば、WIPのコントロールは必ずしもうまくいっているとは言えない。なぜか?
生産管理が生産計画基準となっているためではないか、と考えられる。生産計画固定で平準化が可能な環境条件であれば変動を小さくすることができるが、生産計画がコロコロ変わったり、受注生産で注文が入るたびに生産計画が更新(変更)されたりする環境では変動幅の拡大は避けられない。また生産性を上げようと日程計画の隙間がほとんど見えないほど稼働率を上げる。その結果WIPは増加し続けることになるが、その増加を抑制するメカニズムを意識的に組み込んでいる事例はほとんどない。
少し前置きが長くなったが、生産計画が固定できない生産環境では、WIPを抑制する仕組みが必要となることを確認しておきたい。WIPを制限するのは何のためかと言えば、「フロータイムの跳ね上り」を抑えるためである。
では、WIPの制限によりFTがどの程度短くなるのかをシミュレーションで確かめてみる。前回と同じ10工程直列バランスラインで、投入時間間隔は指数分布、処理時間はk=2のアーラン分布で、WIP制限なし、50個、40個、30個、20個の場合、稼働率に対するFTの変化をみてみる。結果の1例を図28に示す。WIPの制限により、FTの跳ね上がりが抑えられているのが確認できる。
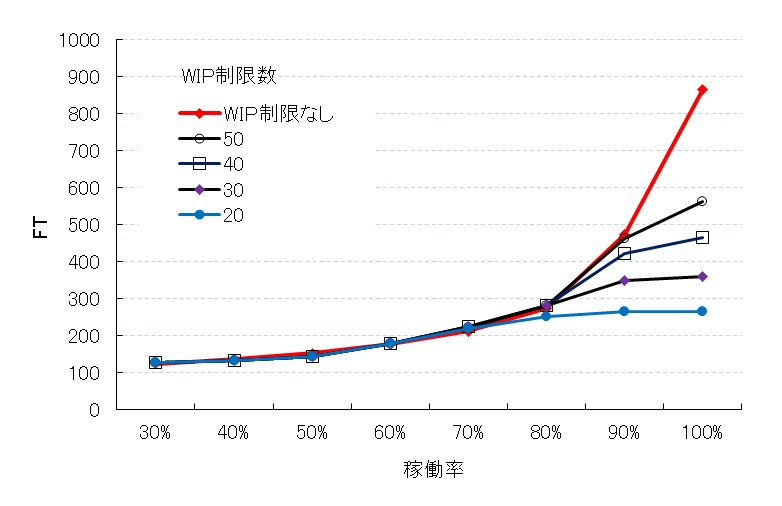
図28 WIP制限によるFTの抑制効果
ここで留意しなければならないことがある。FTは投入から完成までの時間である。それは確かに短くなるのであるが、短くなる分は、投入口で待っているのである。投入制限することで、FTが短くなる分、投入口での待ち時間が長くなるだけで、両方合わせるとほとんど同じ。投入制限による実質的な生産リードタイム(処理時間+待ち時間)の短縮はほとんどない。
WIP制限による実質的な生産リードタイムの短縮はできないが、WIP制限の意味はある。それは、投入後のFTのコントロールができるようになることと、投入口で待つワークの状態をみて、納期調整、受注調整、生産能力調整などの策をとることができるからである。制限するWIP数をU-WIPと呼ぶことにする。
実際は、U-WIPによる投入制限と生産能力の調整の両方を組み合わせて使うことになる。
6、生産ライン内の流れをTIPチャートでみる
生産ラインの特性を生産率(TH)、フロータイム(FT)、仕掛(WIP)で捉えてきた。大枠を捕まえることはできたが、進捗管理はどうするか。進捗管理をするためには、生産ライン内をワークがどのように流れるかをみる必要がある。それをみるのにTIPチャート(Time In Process Chart)が便利である。
10工程直列ラインで処理時間が一定で変動がない場合、生産ライン内をどのような時間経過で流れるのかの1例を図27に示す。処理時間が10分一定のバランスラインで投入間隔が10分一定の時(投入負荷100%)、黒線で示す時間経過を経て、100分後に完成する。投入間隔を6.7分一定(投入負荷150%)にして5番目、10番目、15番目に投入したワークの時間経過は茶色の線で示す。入口工程で待っている様子が分かる。ボトルネックライン(処理時間P5;10分、他は6分)では、水色の線で示したように、P5のボトルネック工程前で待っている様子が分かる。
このように、処理時間や投入間隔に変動がない場合、どの工程にいつ、ワークが到着するか、正確に予測でき、工程ごとに何時から何時まではこの仕事、といった生産スケジュールで作業を進めることができる。生産管理が計画基準であるべきだという根拠である。
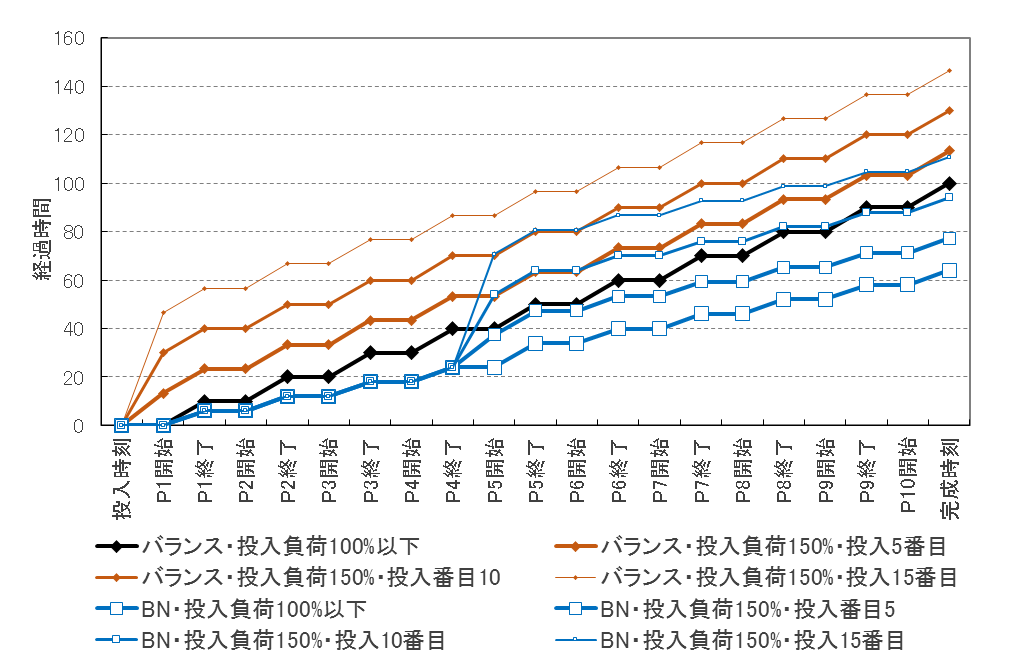
図27 投入間隔と処理時間が一定の場合の各工程通過時刻の一例
処理時間や投入間隔がばらつく場合はどうなるか。投入間隔を平均10分の指数分布、処理時間を平均10分のアーラン分布(k=2)で変動させたとき、各工程の通過時間がどうなるかをシミュレーションしてみる。結果の1例を図28に示す。例えばP6工程の終了時間をみてみると、60分から150分のバラツキがある。あるいは、投入後100分の時点をみてみると、P4工程で処理が終わるワークがあるかと思えばP10工程で処理が始まるワークもある。
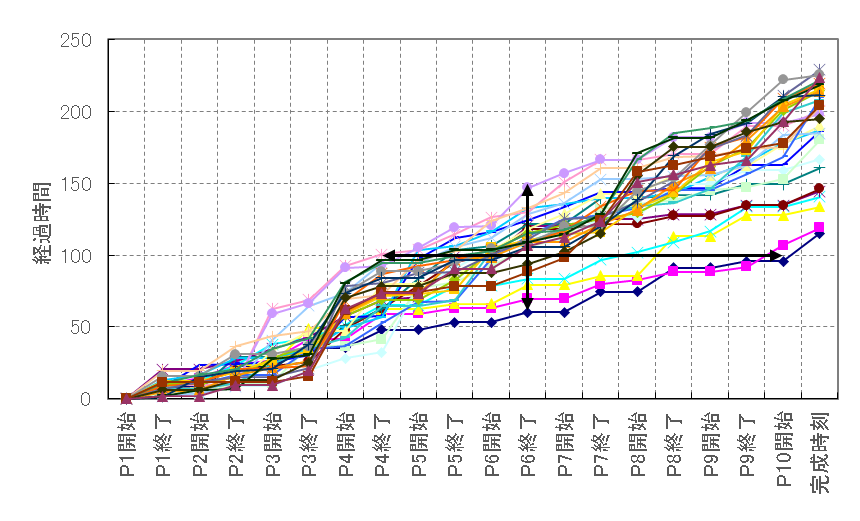
図28 投入間隔、処理時間が変動するときの各工程通過時刻の一例
投入時間や処理時間に変動がない場合、何時から何時までこの仕事という生産スケジュールに従って作業を行うことができるが、変動がある場合、何時から何時までこの仕事と指定したところで、ワークが流れてこなかったり、流れてきてもほかの仕事で忙しかったりで計画通り作業をすることは難しい。計画基準の生産管理が機能しない主な理由である。
どうするか。策を見つけるためには、生産ラインの中をどのようにワークが流れるのかを知る必要がある。直列10工程からなる次の生産ラインをモデルに検討を行う。各工程の平均処理時間とその変動係数および負荷率が既知である。P3とP4の間は、200分間に一度、ワークをまとめて搬送する。また、投入制限仕掛数(U-WIP)は40個である。尚、表中、負荷率はこれまでの稼働率と同じ意味である。
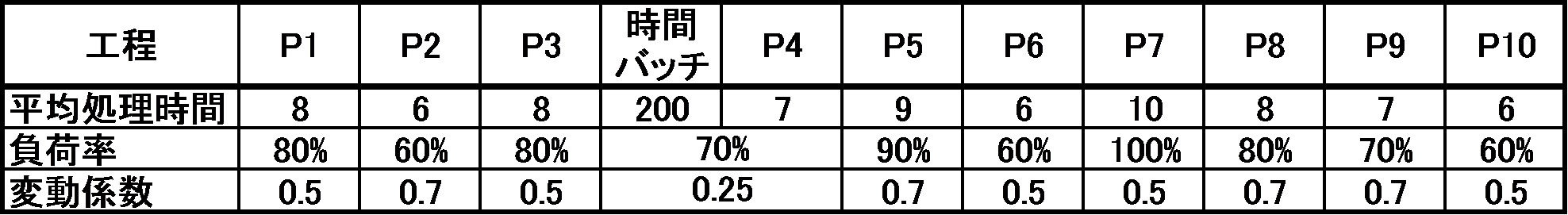
表1 生産ラインの条件
先ず、シミュレーション結果からみてみる。図29は経過時間の最長値と平均値のシミュレーション結果の1例である。
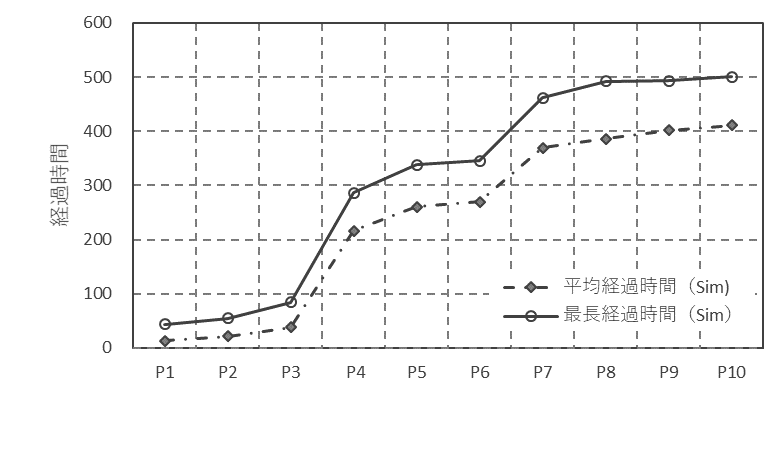
図29 各工程の経過時間のシミュレーション結果
ワークの流れる時間が工程の平均処理時間、その変動係数、負荷率とどのような関係にあるのか、詳しくみてみる。ここで注目するのはU-WIPである。U-WIPで投入制限がかかればWIPはU-WIPより多くはならない。フロータイムがWIPに比例することから、WIPをU-WIPに固定して、フロータイムの簡易計算をしてみる。
簡易計算の手順は次の通り。
① 変動係数の平均(![]() )を求める
)を求める
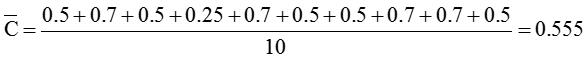
② 負荷率≦90%の工程のWIPの合計を求める
時間バッチのあるP4およびボトルネックのP7を除く各工程のWIPを、負荷率が低い領域ではU-WIPの影響を受けにくい性質を利用して次の式で求める。
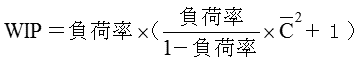
計算結果を表2に示す。

表2
WIPの合計は12.6となる。
③ ボトルネック工程の負荷率を求める
ボトルネック工程の負荷率を求めるためにボトルネック工程に滞留するWIPを算出する。P4とP7以外の工程のWIPを②で算出した。U-WIPは40個であるから、P4とP7に滞留するWIPの合計は40-12.6=27.4(個)となる。次に、P4とP7それぞれに滞留するWIPを求める。
時間バッチ工程P4のWIPを求める式

と、ボトルネック工程P7のWIPを求める式
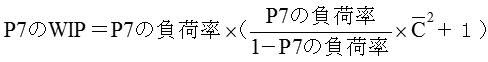
(P4のWIP)+(P7のWIP)=27.4
の2次方程式を解いてP7の負荷率を求める。(式を展開し解を求めるのが煩雑な場合、エクセルを使って解を探す方法も便利である)
計算結果はP7の負荷率=96.84%となる。
④ 平均投入間隔を求める

U-WIPでWIPが一定となる状態では、CONWIPと同じ状態となり、工程を通るワークの平均時間間隔は一定となる。これは、複数の抵抗器を直列につないだ回路を流れる電流値はどの抵抗器でも同じであるのと類似している。
⑤ 工程毎の平均フロータイムを求める
平均フロータイム=平均投入間隔xWIP
計算結果を表3に示す。
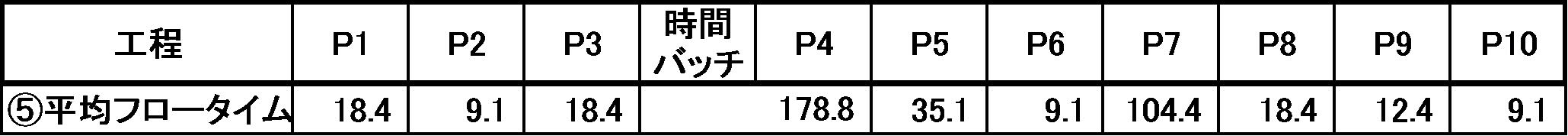
表3
⑥ 平均経過時間を求める
各工程のフロータイムの累積を求める。表4に結果を示す。
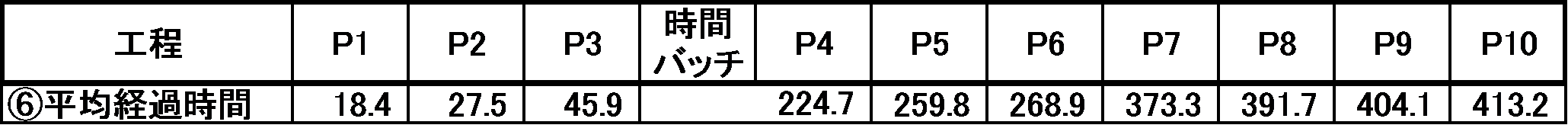
表4
⑦ 各工程のフロータイムの分散を求める
フロータイムの分散=BNの処理時間の分散 x(WIP+1)
BN(P7)の処理時間の分散は次の式で求める。
![]()
計算結果を表5に示す。
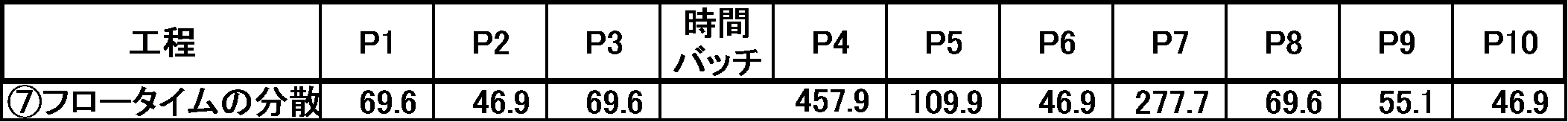
表5
⑧ フロータイムの分散の累計
フロータイムの分散の累計を求める。結果を表6に示す。
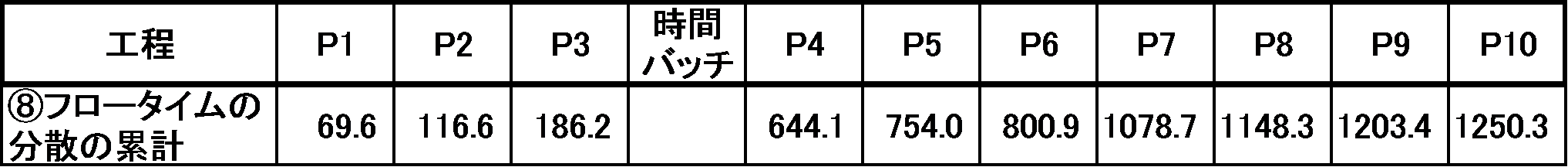
表6
⑨ 最長経過時間を求める
次の式で経過時間の最大値を求める。
![]()
ココでは標準偏差の3倍を最大値としたが、標準偏差の何倍を最大値とするかは状況に応じて決める。表7に結果を示す。
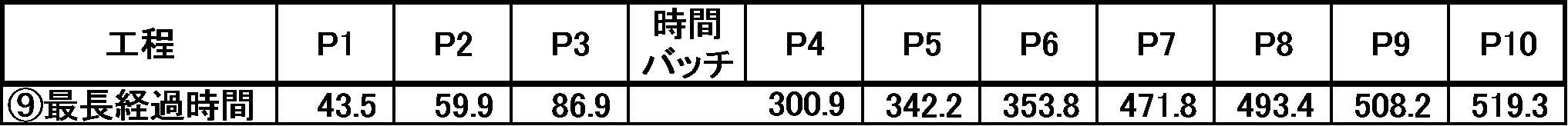
表7
これで各工程を通過する平均時間と最長時間が算出できた。
<TIPチャートで簡易計算結果とシミュレーション結果を比較>
簡易計算結果とシミュレーション結果を表8に示す。良く一致することがわかる。
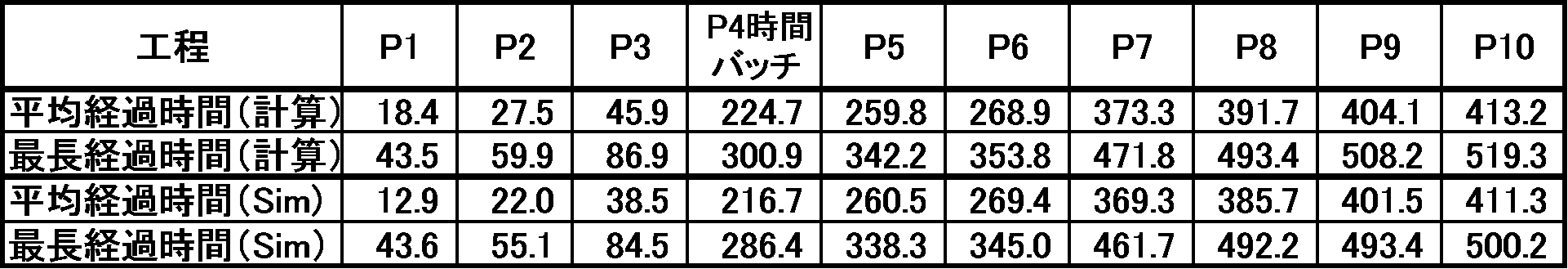
表8 簡易計算結果とシミュレーション結果の比較
これをTIPチャートにしたのが図30である。
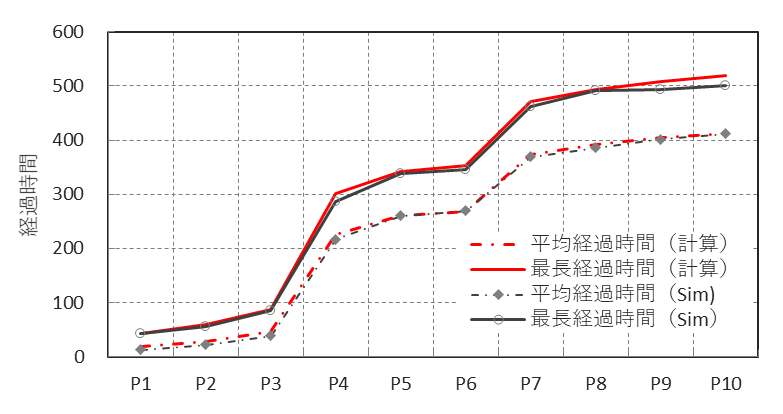
図30 簡易計算結果とシミュレーション結果の比較
7、フロータイムをコントロールする
TIPチャートでは投入から完成までのフロータイムの平均および最大値や途中工程毎の通過時間の平均と最大値がわかる。FITチャートではC-WIPとU-WIP、フロータイムや生産率のおおよそがわかり、生産ラインの特性のアウトラインを把握することができる。これで生産ラインの管理限界を知ることができるようになった。しかし、それだけでは不十分である。
一つの生産ラインでは様々な製品がつくり出される。特に受注生産環境下では異なる顧客の納期を満たさなければならない。その時々で、製品により、顧客により異なったフロータイムで生産を管理しなければならない。
生産スケジュールによる時間管理が出来ないとき、フロータイムをどのようにしてコントロールするかをみてみる。
<残時間比を優先度として使う>
生産ラインを流れるワークを動的に管理するためには、各ワークにガイドラインとなるフロータイムの情報を与えておかなければならない。これを基準フロータイムと呼ぶことにする。(ここでは生産ラインの基本特性について説明しているので、基準フロータイムと呼んでおくが、実際に生産ラインの設計をするときなどは、「標準生産リードタイム」など、使い慣れた表現をする場合が多い)
生産の進捗を管理するためには現在時刻での進捗情報が必要である。完成時刻から基準フロータイム分遡った時刻が投入時刻となる。現在時刻と投入時刻の差を経過時間、現在時刻と完成時刻の差を残時間とする。(図31参照)
図31 基準フロータイムと残時間
基準フロータイムに対する残時間の比を残時間比とする。

基準フロータイムが20日、投入日から7日が経過していれば残時間は13日、残時間比は65%となる。完成予定日を5日過ぎても完成していないときの残時間比はマイナス25%となる。
この残時間比を優先順の制御に用いる。残時間比の数値が低いワークの優先順が高いと判断する。
<優先制御の効果をみる>
優先制御機能をシミュレーションで確かめてみよう。投入間隔は指数分布、処理時間はk=2のアーラン分布。10工程直列バランスラインにRFT400、RFT600、RFT1000の3種類の製品を投入してみる。3種類の製品は全く同一仕様の製品である。違いは、それぞれ400分、600分、1000分とそれぞれ異なった基準フロータイムが設定されていることである。3種類の数量比率はRFT400が23%、RFT600 が27%、RFT1000が50%で、投入のタイミングは3種類それぞれ独立で指数分布に従う。
① 優先制御がない場合
初めに、残時間比による優先制御はしないで、フロータイムがどうなるかをみる。
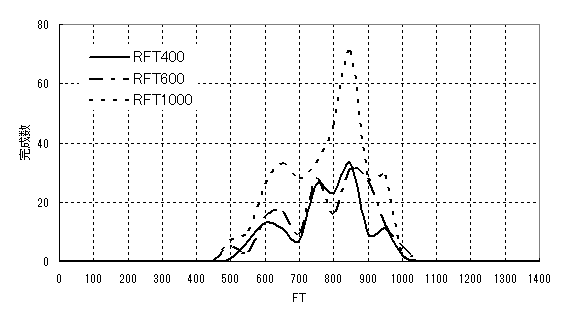
図32 優先制御がない場合のフロータイムの分布
図32に示すように、3種類ともフロータイムはほぼ同程度である。
② 優先制御がある場合
今度は、各工程で残時間比による優先制御を行ってみる。優先制御の方法は各工程の前に複数の仕掛がある場合、残時間比の低い順に処理する。仕掛がない場合は残時間比に関係なく、ワークが到着したら直ちに処理を開始する。
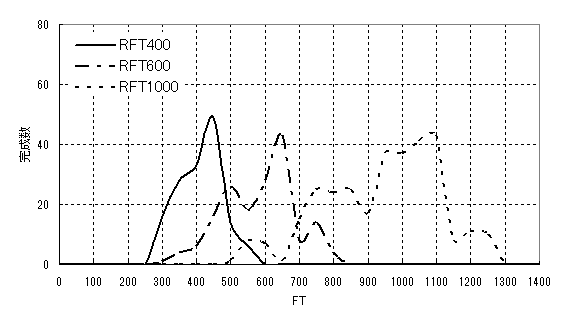
図33 優先制御がある場合のフロータイムの分布
優先制御をした場合の結果を図33に示す。基準フロータイムの短いRFT400は左寄りの短いフロータイムで完成し、次にRFT600、そしてRFT1000が右寄りの長いフロータイムで完成する。優先制御が機能していることがわかる。もうひとつ注目しておきたい特性は、RFT400は優先制御をすることによってフロータイムが短い方に移動したが、RFT1000は逆に長い方に移動していることである。
<WIPの制限でフロータイム制御が受ける影響>
フロータイムの上限を規制するために、U-WIPで投入制限をする方法が有効であることを先に確かめた。今度は、U-WIPで投入制限をすると、ワークごとに異なった複数のフロータイムのコントロールはどうなるか、シミュレーションしてみる。U-WIPを50個として、その他は前と同じ条件でのシミュレーション結果を図34に示す。全体がフロータイムの短い方向にシフトしているが、フロータイムの長い方がWIP制限の影響を受けやすいようである。
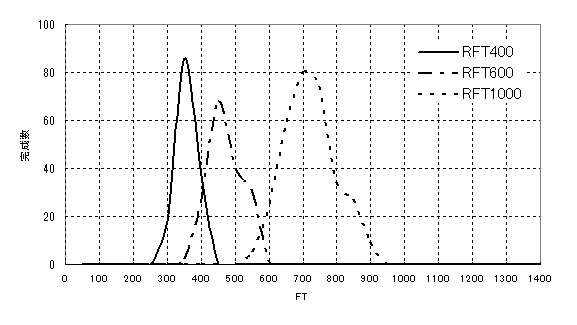
図34 U-WIPが50個でのフロータイムの分布
さらに、U-WIPを振ったときにどうなるか、一例を図35に示す。基準フロータイムによって傾きは異なるが、U-WIPとフロータイムはほぼ比例関係にあることがわかる。U-WIPでの投入制限によって異なる複数のフロータイムをまとめてコントロールすることができることを示している。
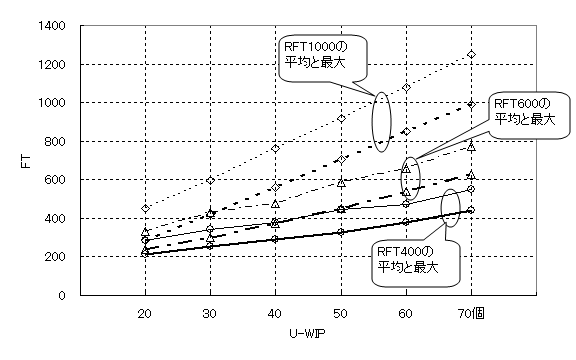
図35 U-WIPに対するフロータイムの変化
図36に示すTIPチャートはU-WIPを40個で投入制限したときの、RFT400、RFT600、RFT1000の各工程の通過時間を示している。RFT400は待つ時間がなくスイスイ流れるが、RFT600やRFT1000はところどころの工程で待っている様子がわかる。
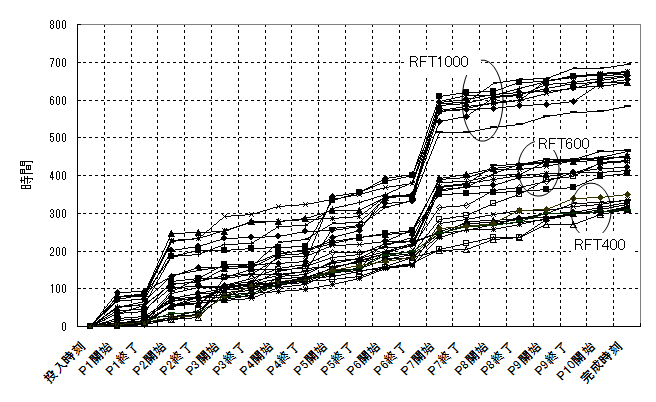
図36 U-WIP40個のときのRFT400、RFT600、RFT1000の各工程の通過時間
8、計画基準から需要基準への転換
生産ラインの物理的基本特性をみてきた。生産スケジュールを秒単位で詳細に立てたとしても、スケジュール通り作業を進めることは至難の業。原理的には不可能である。
つくれば売れる生産者優位の市場環境では、工場の生産性を優先した計画基準の生産管理が理に合う。しかし、それは数十年前までの話。市場が消費者優位になって久しい。にもかかわらず、生産管理の在り方は昔のままである。
DX(デジタルトランスフォーメーション)を聞かない日はないほどデジタル化の波が激しく押し寄せているが、巷にあふれる生産管理の本は、相も変わらぬ古典的生産管理論のまま。
買い手市場では古典的生産管理論は成り立たないことはわかっても、ではどうすればいいのか。どこに解決策の手がかりがあるのか。
方向性を見失ったら、原点にかえる。原点とは、
「生産ラインの基本特性」
を再確認すること、、。
計画基準から需要基準への転換には、避けて通れない原点回帰ではないのか。