No.86 安全在庫は考えない方がいい

図１をご覧ください。在庫減少の平均とそのバラツキから欠品となる条件を模式的に描いた図です。在庫管理ではよくお目にかかる図ですが、この背後に現在の在庫管理の陰が映っているように思います。不細工さというか、チグハグさというか、、ださい在庫管理の素性が、、。

発注方式は、定量発注とか定期発注とかありますが、比較的簡単な発注点方式を例に考えてみたいと思います。

発注点は次の式で計算すると説明されています。

発注点＝（補充時間の平均出荷量）＋（安全在庫）

早速出てきました。安全在庫。で、安全在庫は次の式で計算します。

安全在庫＝（安全係数）×（√補充時間）×（単位期間での需要の標準偏差）

この式を簡単にするために、補充時間と単位期間をどちらも１とします。そうしますと、

安全在庫＝（安全係数）×（補充時間での需要の標準偏差）

と簡単になります。でもまだ、わかりづらい。安全係数です。

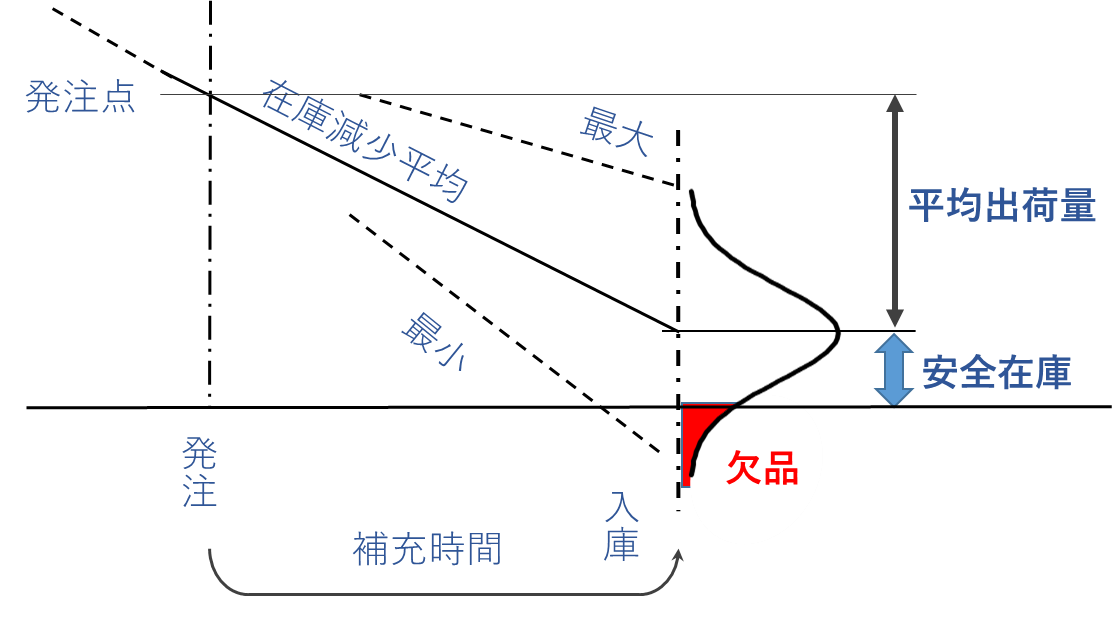
図１　安全在庫説明の一例

安全係数とは図１の赤色で示す欠品率を決めるための係数です。表１に示すように許容欠品率、あるいはサービス率（＝1－許容欠品率）に対して決まっている係数です。

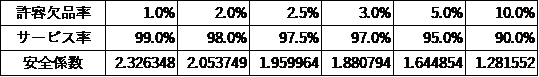
表１　安全係数表

具体的な数値で計算してみましょうか。ある製品の需要の平均が10、標準偏差が2.5だとします。サービス率は97％としましょう。安全係数は1.88ですので、安全在庫は、

安全在庫＝1.88×2.5＝4.7

発注点は、

発注点＝10＋4.7=14.7

で、切り上げて15ということになります。サービス率が90%なら安全係数が1.28なので、発注点は、10+1.28×2.5=13.2 で、切り上げて14となります。

サービス率を設定し、安全係数を探して安全在庫を計算し、平均を足して発注点を求める。それほど難しい計算ではありませんが、安全係数って、どこにあるの？　探してみました。日科技連が発行している数値表の中の正規分布表に出ています。計算よりも安全係数を見つける方が大変、、。

日科技連の数値表といえば、品質管理では必需品でした。昭和の話です。今どき、こんな数値表なんかなくてもエクセルでNORM.S.INV(サービス率)で簡単に求められます。NORM.S.INV(0.9)だと1.281551566と、瞬時に出てきます。

ということは、安全係数だの安全在庫だのと言わず、発注点をエクセルで一発で求めることができるのでは、、、。探してみました。NORM.INV(サービス率、平均、標準偏差)という関数がみつかりました。サービス率97%で発注点を計算してみると、需要の平均は10、標準偏差は2.5ですから、

NORM.INV(0.97,10,2.5)=14.70198

となりました。サービス率90%では、

NORM.INV(0.97,10,2.5)=13.20388

となりました。数値表の安全係数を使った時の答えと若干異なりますが、エクセル計算の方が正確ですよね。

安全係数を使う必要もなければ、安全在庫を計算して平均値を加えるという計算も必要ありません。需要の平均と標準偏差、それからサービス率がわかれば簡単に発注点を求めることができます。発注点は整数ですので、四捨五入する場合は、

ROUND(NORM.INV(サービス率、平均、標準偏差),0)

切り上げのときは、

ROUNDUP(NORM.INV(サービス率、平均、標準偏差),0)

とすればいいでしょう。

考えてみれば当たり前の話なんですがね。補充時間での需要分布の累積確率がサービス率なので、指定した平均と標準偏差に対する正規分布の累積分布逆関数の値を求めればいいわけです。

もう少し掘り下げて考えてみましょう。この計算は、需要分布が正規分布することを前提としているんですね。では、正規分布で近似できないときはどうすればいいんでしょう。正規分布で近似できない場合の例を図２に示します。黒線のカーブは正規分布に近似できますが、平均が小さくなると分布の山頂は左に寄ってきます。需要は実数を扱いますので、その分布はゼロ以下には分布しないと考えますと、ゼロの壁に押し付けられるように分布は歪んできます。水色のカーブが1例です。どう見ても正規分布とは言えないんじゃないかと思います。現実的には、間欠需要のときなどにこのような需要カーブとなります。

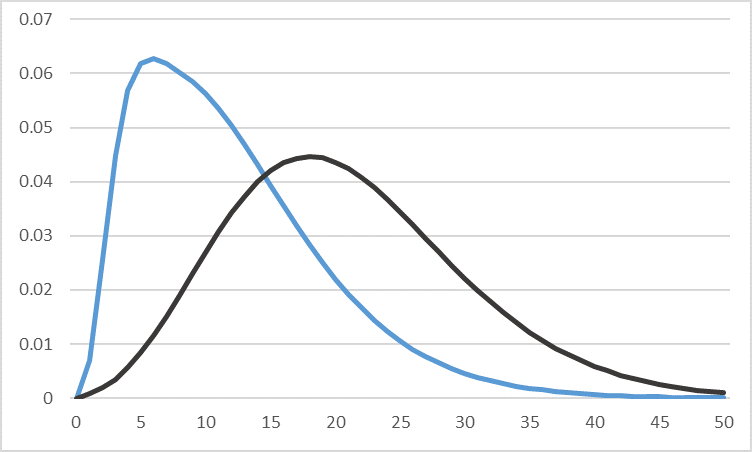
図２　需要分布形状例

正規分布の代わりになる分布はないんでしょうか。探してみました。ガンマ分布はどうでしょうか。図３に、図２の水色のカーブの平均と標準偏差が同じ正規分布とガンマ分布を重ねてみました。正規分布よりはガンマ分布の方が似ているでしょ。正規分布のゼロの部分が跳ね上がっているのは、マイナス側の確率をゼロの確率に集計したためです。

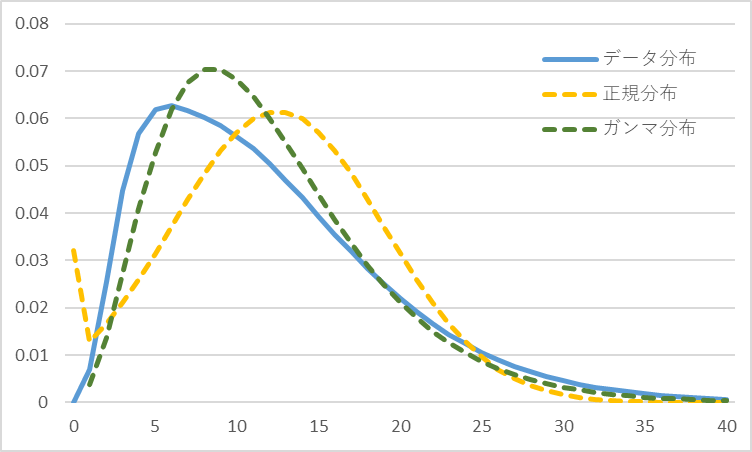
図３　データ分布と同じ平均、標準偏差の正規分布とガンマ分布

ガンマ分布が正規分布より良さそうだ、ということはわかりました。では、ガンマ分布の累積分布逆関数の値を求めるのはどうするのか、ですが、これもエクセル関数を利用できます。GAMMA.INVという関数があります。

この関数を使って、サービス率が90％、95％、99％での在庫量を計算してみました。結果は表２のようになりました。元のデータ分布に対して、ガンマ分布の方が近い値が出ます。

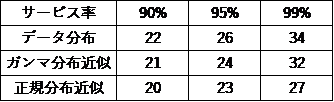
表２　データ分布に対するガンマ分布と正規分布の比較

発注点の求め方から話を始めましたが、安全在庫という考え方は、在庫管理のいたるところで出てきます。適正在庫＝サイクル在庫＋ミニマム在庫、なんて説明されていますが、平均＋安全在庫と同じ意味でしょう。

必要な資材量を算出して、その後に起こるであろう変動に対して多めに手配しておく。多めに手配する分が安全在庫。つまり、必要量（平均）＋安全在庫。生産、在庫管理の歴史の中で出来上がった考えなんでしょうね。安全在庫も、初めは、このぐらい、とか言って勘や経験で決めていたんでしょうね。それではあまりにも不細工なので、分布の王様、正規分布の性質を利用して、サービス率を設定し、欠品を起こさない資材量を求めるようになった、のではないのかな。

サービス率→安全係数→安全在庫→発注点（適正在庫）設定という手順は計算方法だけではなく、在庫管理の考え方として定着している感があります。需要分布の平均と標準偏差が既知であれば、サービス率に対する発注点（適正在庫）は一発で、エクセルで出てきます。ガンマ分布関数を使えば、間欠需要など正規分布しない場合でも、かなり精度良く簡単に計算できます。安全係数とか安全在庫とか、考えなくたっていいし、考える必要もなし。

需要分布を固定部分（平均）と変動部分（安全在庫）に分けて捉える現行、在庫管理のやり方って、どうみてもスマートじゃないですよね。どうしてこのような不格好な在庫管理になったのか、、ではどうすればいいのか、などは、次回にでも、、