No.84 間欠需要で納入リードタイムが変動する場合

間欠需要は、注文件数そのものが少ないこともあり、実績データも限られている場合が多いと思います。データが少ないと需要分布形状を特定することは難しくなります。そんな時でも、補充時間での需要分布形状を推計し、サービス率が1％刻みで、適正在庫を算出する方法を前回、前々回、紹介しました。

今回は、さらに一歩踏み込んで、補充時間がバラツク場合の適正在庫を計算する方法を紹介します。

補充時間とは、在庫から出庫して、その分が補充されるまでの時間です。通常は発注から納入・入庫までの時間（納入リードタイム）と発注間隔（発注サイクル）で構成されます。間欠需要の場合の在庫補充発注は頻度も低く、イレギュラーになりがちです。納入側も対応がとりづらく、納入リードタイムも変動しやすくなります。最長の納入リードタイムで計算する方法も考えられますが、それだと、在庫は多くなってしまいます。

補充時間がバラツクとその間の需要はどのような影響を受けるか、表１に示すデータを使って検討してみましょう。

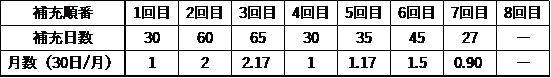
表１　在庫補充に要した日数（下段は月数換算値）

表1のデータを度数分布で表すと図1のようになります。尚、30日の相対度数は0.286、他の相対度数はすべて0.143となります。

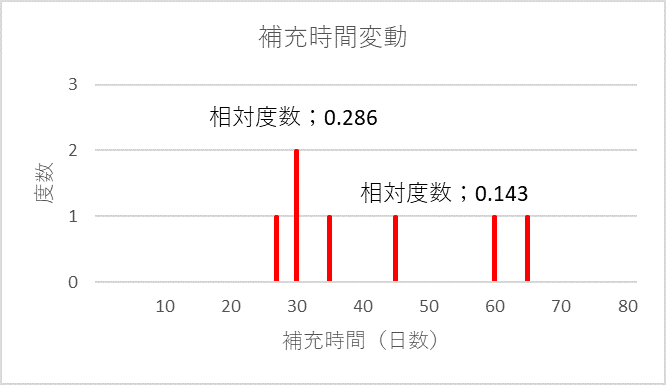
図1　在庫補充日数の度数分布

需要データはこれまでと同様、表2のデータを使うことにします。補充時間の変動の影響は、補充時間が変動しない場合と比べると分かりやすいと思います。先ず、補充時間が一定の場合の受注件数の分布を推計することにします。補充時間の一定値として、平均値1.39カ月を使うことにします。計算方法は前回（No.83）説明してありますので、そちらを参照ください。

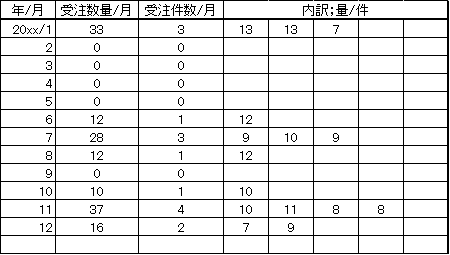
表２　受注データ

補充時間が変動する場合、表１の下段にある月数補充時間ごとの受注件数の分布を試算します。それぞれに相対度数を乗じて、合算します。補充時間が固定された場合と変動がある場合の分布との比較を図２に示します。補充時間がバラツクことで、受注件数の分布のすそ野が広がるのが確認できます。

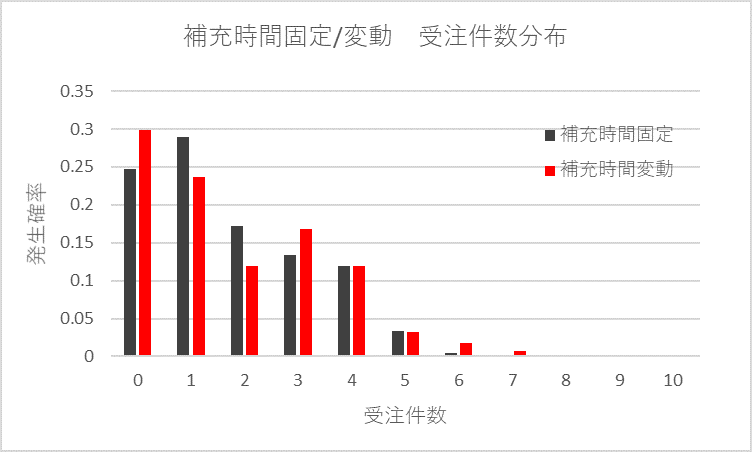
図２　補充時間の変動有り無しでの受注件数分布比較

補充時間が変動する場合の受注件数の分布と表２に示される量/件の分布で需要分布を計算すると、図３に示すような結果となります。補充時間が変動することで需要のバラツキも大きくなることが予測されますが、その差はそれほど大きくはないようです。サービス率90%では補充時間変動無しの必要在庫は44個、有のそれは46個ですが、サービス率が99％ではそれぞれ55個と65個となり、差が大きくなります。

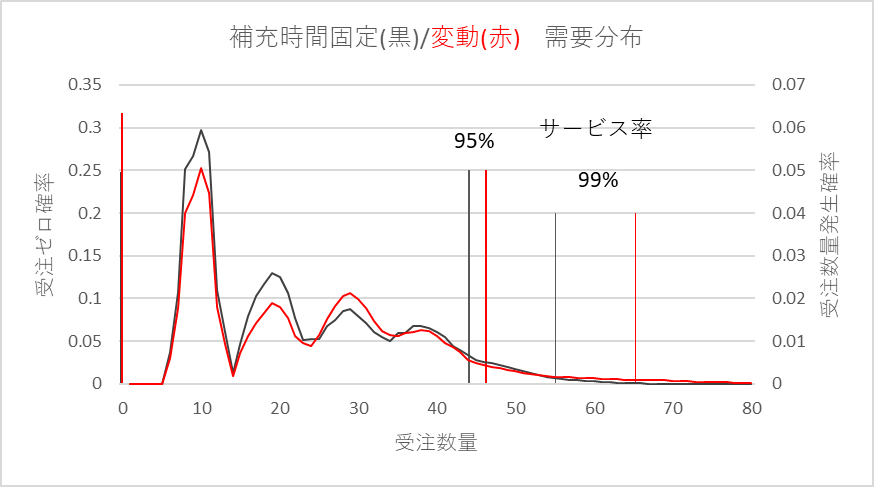
図３　補充時間変動有り無しでの需要分布比較

間欠需要での適正在庫の算出方法について、3回に分けて（No.82、83、84）検討してまいりました。間欠需要は、サプライチェーンの中では、決して珍しいことではなく、いやむしろ、毎日需要があるような商品よりも売れない日もある商品の方が多いのではないかとさえ思われます。一方、在庫管理側からみますと間欠需要では需要パターンが正規分布とはならず、データ数も少なく、例外とまではいかなくても、厄介者的に扱われてきたのではないでしょうか。

分布形状のパラメータ（平均とか分散など）を一切使わないで、採取された数少ないデータのみを用いて、需要分布形状を推定し、必要在庫（適正在庫）を求めることができます。分布形状のパラメータが不要であるということは、いかなる分布形状でも取り扱うことができることになります。

もちろん、データ量が少なければ誤差は大きくなり、データの質が悪ければ結果の質も低下します。実用的にはどの程度のデータ量があればいいのか、データの質を確保するためのデータ集計方法の指針など、今後の課題としたいと思います。

時間の経過とともにデータは蓄積され、母集団の分布も特定しやすくなります。そうなれば特定された分布のパラメータを使うことができるようになるでしょう。一旦、分布形状が特定されれば、その分布のパラメータを使っての需要分布形状の計算が比較的容易にできるようになります。もちろん、新たに蓄積されるデータと特定した分布形状との整合性は定期的にチュックする必要はあるでしょう。

需要構造の基本要素は受注件数と量/件と補充時間の3つの確率変数です。単位も件数、個数（SKU、ダース、、）、時間（日、週、月、、）とそれぞれ異なり、それぞれ変動し、分布形状もそれぞれ異なります。この3つの確率変数のいずれもが特定できない場合でも適正在庫を計算できますが、現実では、その中のひとつか二つの確率変数が特定できない場合も起こります。つまり、次の3つのケースが出てきます。

* 3つの確率変数がノンパラメトリック
* ノンパラメトリックとパラメトリックが混合する
* 3つすべてがパラメトリック

パラメータを使っての需要分布形状や必要在庫の計算方法については、原理的にはほぼ出来上がっていると思われます。ここで提案するノンパラメトリック手法は、既存のパラメトリック手法と相まって、両者をシームレスカバーする在庫管理論の構築に資するのではないかと期待しております。