No.81　間欠需要パターンのときの需要分布形状

需要の分布形状はどうなっているのだろう、という好奇心でいろいろ調べています。ランダムに来る注文の時間間隔分布は指数分布、ある一定時間間隔で注文件数をカウントすると注文件数（受注件数、来客数）はポアッソン分布する、と仮定してみました。この考え方は待ち行列理論ではお馴染みです。量/件の分布については、定説はないようです。常識的には正規分布かな、と思うんですが、受注数は離散型を想定していることから1以上の領域で分布することになり、マイナス側にも分布する正規分布は適しないと考えました。で、ガンマ分布がいいんじゃないかと思って、選んでみました。

受注件数の分布はポアッソン分布、量/件の分布はガンマ分布として、ある一定期間（1日とか1週間とか、、）の受注数量（需要）の分布はどうなるか。これが前回の検討結果です。量/件の変動係数が小さいと受注数量の分布はデコボコしますが、変動係数が大きくなると滑らかな分布形状となり、正規分布に近似します。安全在庫の大きさを求めるとき、需要は正規分布で計算する理由はここにあり、ですね。デコボコしてていても大枠が正規分布で近似できれば、実用上の問題ないと思われます。

ところが、どんな場合も正規分布に近似できるか、というと、そうではありません。どういう場合、近似できなくなるかといいますと、受注件数の平均が4～5以下のときです。前回も掲載しましたが、図１に受注件数の分布（ポアッソン分布）の一例を示します。平均10の分布は正規分布に近似します。平均5は多少非対称ですが、この辺りまでは正規分布に近似するとしてもいいでしょう。しかし、平均2や1では正規分布とは言えなくなります。

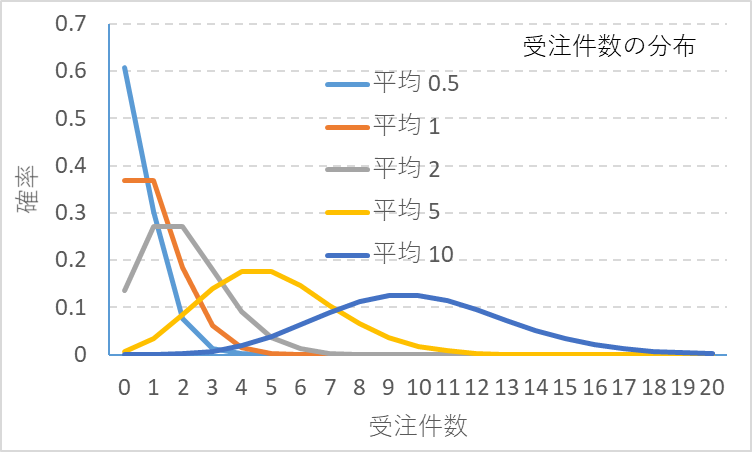
図1　受注件数の分布（ポアッソン分布）

前回の検討結果からもわかるように、受注数量（需要）の分布形状は、受注件数の分布形状の影響を強く受けます。受注件数の分布が正規分布に近ければ受注数量の分布も正規分布に近似できます。受注件数の分布が正規分布に近似できないときはどうすればいいのか、これが今回の課題。

受注件数の平均が５件以下の領域の特徴をみてみます。図１で、例えば、平均１件の分布をみてみます。受注０件の確率が36.8%、1件の確率も36.8%、２件の確率が18.4%、、、となります。件数の観測時間間隔が1日としますと、3日に1日は注文がない日がある、ことを意味します。平均が0.5件であれば受注件数0の確率が60%ですから、5日に3日は注文がない、ということになります。このように、注文のない日がある受注パターンを間欠需要と呼ぶことにします。

今回は、間欠需要での受注数量の分布形状はどうなるのか、調べてみたいと思います。前回つくったエクセル表に条件を入れるだけで、簡単に調べることができます。

先ず、前回とのつながりで、受注件数平均10件、量/件平均５、変動係数0.２での受注数量の分布を再掲します。受注数量分布の平均と分散が同じ正規分布も表示しておきました。ピークがちょっとズレますが、安全在庫を算出するすそ野は正規分布とほぼ同じであることが分かります。

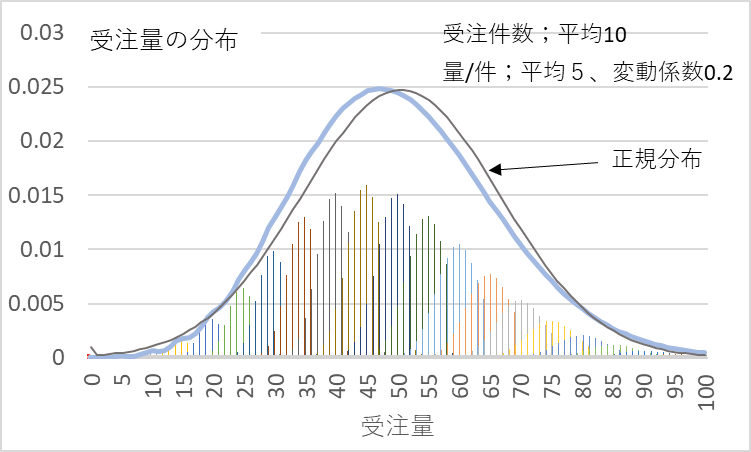
図２　受注件数平均10件、量/件平均５、変動係数0.２での受注数量の分布

次に、受注件数平均を5件にしてみます。その時の受注数量の分布は図３に示すようになります。受注数量（件数）が０件の場合も出てきます。その確率を赤棒で示しています。正規分布の0件の確率は、マイナス件数～ゼロまでの累積確率を示してあります。

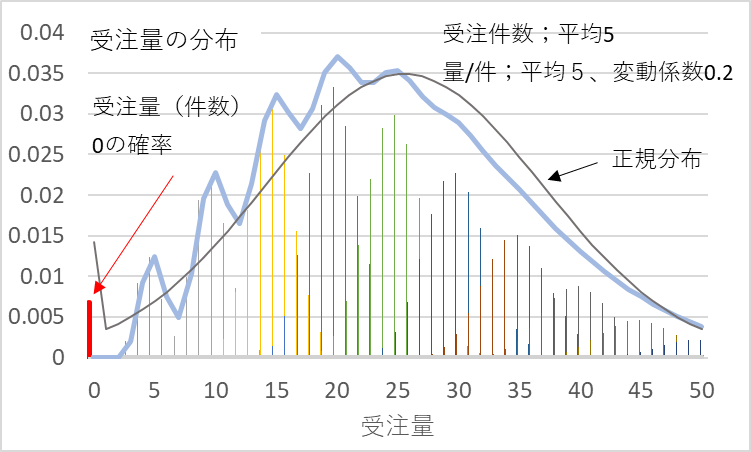
図３　受注件数平均5件、量/件平均５、変動係数0.２での受注数量の分布

次に、受注件数の平均が2件のときの受注数量の分布を図４に示します。

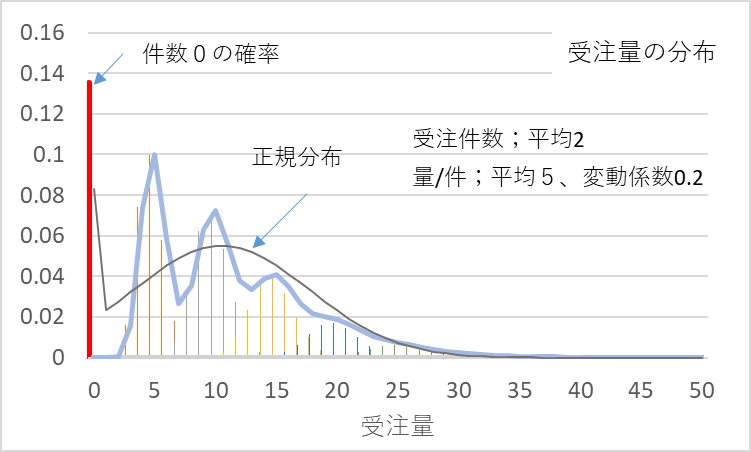
図４　受注件数平均2件、量/件平均５、変動係数0.２での受注数量の分布

さらに受注件数が減って、その平均が1件のとき受注数量の分布はどうなるか、図5に示します。

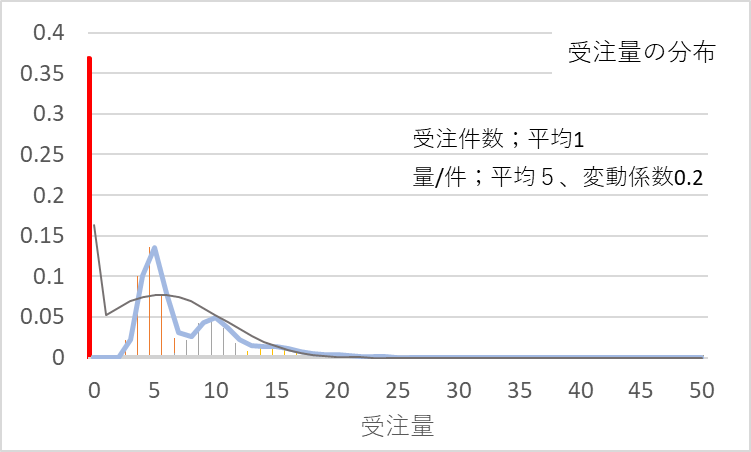
図5　受注件数平均1件、量/件平均５、変動係数0.２での受注数量の分布

次に、受注件数の平均が1件以下、例えば0.5件のときの受注数量の分布の一例を図6に示します。

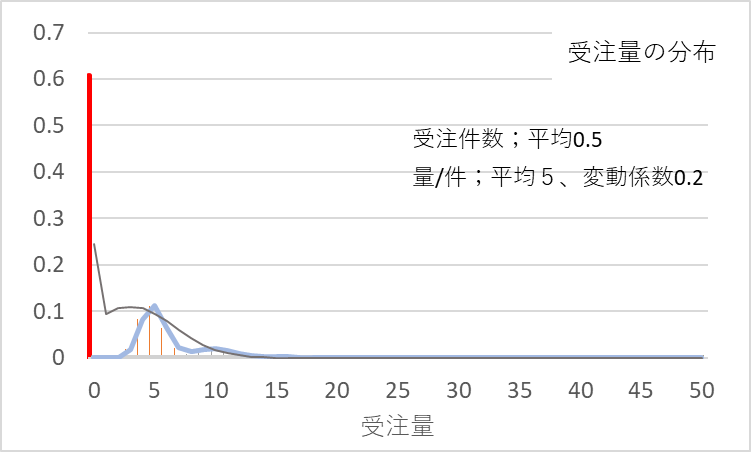
図6　受注件数平均0.5件、量/件平均５、変動係数0.２での受注数量の分布

受注件数が４～５件以下になると受注数量の分布は正規分布とは言えなくなることはお分りいただけたと思います。で、課題は？　そうそう、安全在庫の計算に正規分布が使えなくなる、で、どうするか？　ということです。

考えられる手は、、二つぐらいあるかなぁ～、、。ひとつは、分布のすそ野に注目してみますと、、。需要分布のすそ野も正規分布のすそ野も、重なり合っていますね。正規分布の２σ以上の領域では正規分布に近似するのではないか、と思えるわけです。で、実際は、受注件数が小さくなるに従い、ズレが大きくなるので補正する必要は出てきます。

もうひとつは、正規分布との縁を切って、分布形状そのものから計算する方法です。こちらの方法はどのような分布形状でも、確率分布の形状を示す数値があれば使える可能性があります。例えば、サービス率が95％の適正在庫（必要在庫）はゼロから累積確率が95％のところの値を求めればいいわけです。この方法は、簡単な計算では済みません。専用のソフトでは実際に行われているようです。でも、あまりはやってはいないようですが、、。

間欠需要での需要分布については、巷でも諸説があって、適正在庫の算出方法もいくつか提案されています。これまでに得られた知見を基に、間欠需要の問題を考えてみようか、と思います。