No.80　件数と量/件の分布から受注量の分布を求める

必用在庫量（適正在庫量）を算出するうえで必要な情報は納入リードタイム間（より正確には“納入リードタイム＋発注まとめ時間”）の受注量です。受注量は、受注件数と1件当りの受注量（量/件）で算出されます。今回は受注件数、量/件が変動するとき、受注量はどのようになるのか、それぞれの分布形状に注目し、エクセルで計算してみたいと思います。

先ず、検討しなければならないのは、量/件の分布モデルです。受注件数はゼロ以上の整数値ですが、量/件は１以上の整数値をとる、とします。

正規分布はマイナス側にも分布しますので、１以上の分布としては不適です。片側の分布はいろいろありますが、適用範囲が広そうなので、ガンマ分布を選んでみます。しかし、ガンマ分布はゼロ以上１未満の領域である値をもっているので、これを補正することにします。分布形状の1例を図１に示します。平均はいずれも５、変動係数を１、0.7、0.5、0.1の場合のそれぞれの分布形状です。

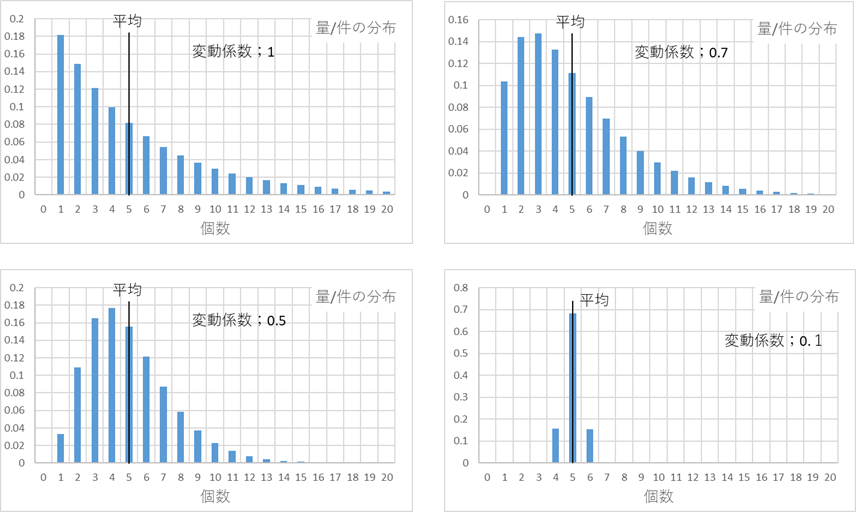
図１　量/件の分布形状モデル　平均５個、変動係数；１、0.7、0.5、0.1

次に、受注件数の分布モデルを検討します。マイナスの受注件数はありません。ゼロ以上の片側分布となります。受注件数の分布を考えるとき、その構成要素を理解しておくことが重要です。注文の到着時間間隔と観察時間間隔です。注文の到着時間間隔が1時間、観察時間間隔が5時間であれば受注件数は5件、観察時間間隔が10時間であれば10件、という関係です。

観察時間間隔は1日とか1週間とか、一定の時間間隔が一般的ですが、到着時間間隔は通常ランダムに変動します。ランダムな到着時間間隔の分布としてよく使われるのが指数分布です。到着時間間隔が指数分布する注文を一定時間間隔で観察すると、注文件数の分布はポアッソン分布することが知られています。その一例を図２に示します。平均が５件付近以上では正規分布に近似できますが、それ以下では片側分布となりますので、留意しなければなりません。

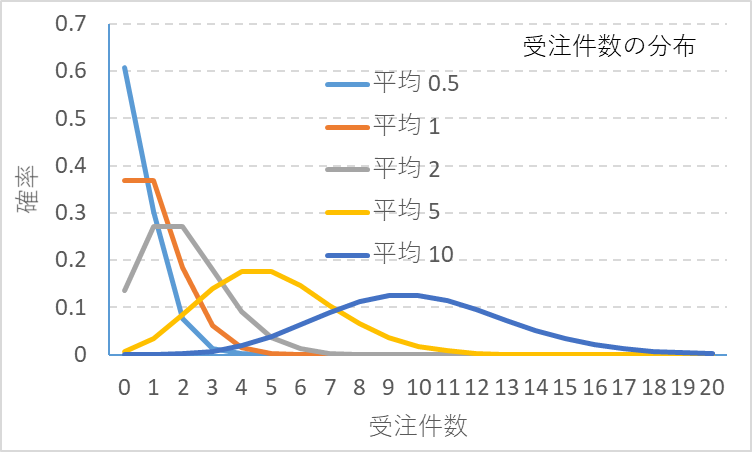
図2　受注件数の分布モデル

先ず確認しておきたいことは、受注件数の分布モデルと量/件の分布モデルは異なることです。受注件数が増える場合と量/件が増える場合とでは、平均受注量の増加が同じだとしても、受注量の分布形状が異なるのではないか、と思われます。分布形状が異なれば、受注量の平均は同じでも欠品率に対する安全在庫量は異なってきます。

受注件数と量/件の分布モデルを選定しました。次に、受注件数と量/件の分布がどのようなメカニズムで受注量の分布を形成することになるのかを考えます。

受注件数の分布について、もう少し詳しくみておきます。図１をみますと、連続分布のようにみえますが、実際は、離散型の分布です。同じデータですが、図２に示すように、棒グラフで表した方がイメージしやすいと思います。

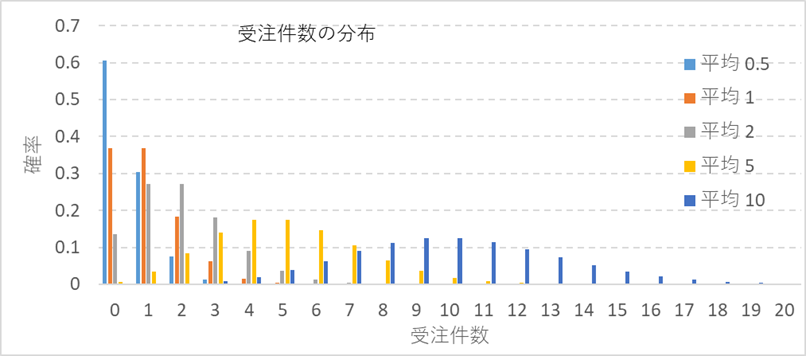
図２　棒グラフで表す受注件数の分布

受注件数の平均が10件、量/件が１個で固定の場合は、受注量の分布は図２の平均10のポアッソン分布となります。では、量/件が５個で一定の場合はどうなるか、その一例を図3に示します。例えば受注件数が4件では、1件の受注で5個ですから、4件の受注では受注量は、5+5+5+5=20個となります。6件の注文ならば、5+5+5+5+5+5=30個、、、となります。受注量全体の分布形状は図３に示すようになります。

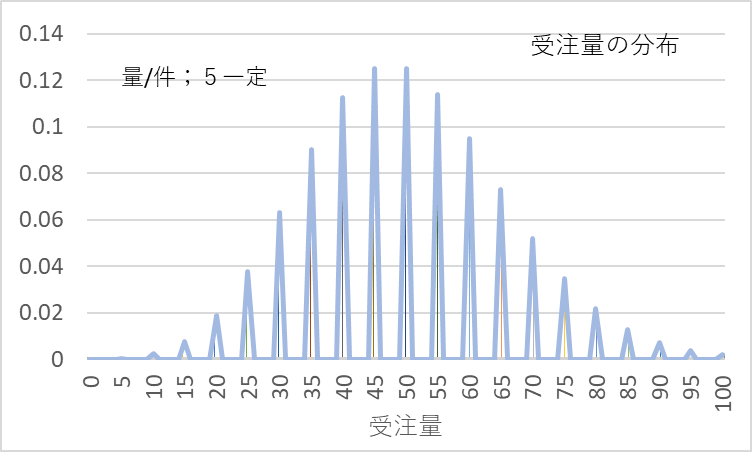
図３　量/件が５、一定のときの受注量の分布

量/件に変動を加えるとどうなるか。量/件の平均は５個のままで、変動係数を0.1にしたとき、量/件の分布は図１の右下のようになります。平均5個、変動係数0.1の量/件の分布からランダムに抜き取る（受注する）ときの値が、その受注の注文数量となります。受注件数が複数件の場合は、抜き取った（受注した）値の合計が受注数量となります。

分布形状について考えてみます。ガンマ分布に従う確率変数をX１、X2、X3、X4、、として、X1+X2、X3+X4、、、の分布はどうなるかといいますと、これもガンマ分布となります。これは再生性と呼ばれる性質です。この性質がありますので、受注件数回の和の分布もガンマ分することになり、エクセル関数で計算することができます。

例えば受注件数が6件では、量/件の分布から6回サンプリングされ、その和の分布となります。受注件数が10件では１０回加算された分布となります。右側に行くに従い、分布が広くなっていきます。

全体の受注量の分布は、それぞれの件数の分布を重ね合わせた分布となります。受注量の分布の一例を図４に示します。

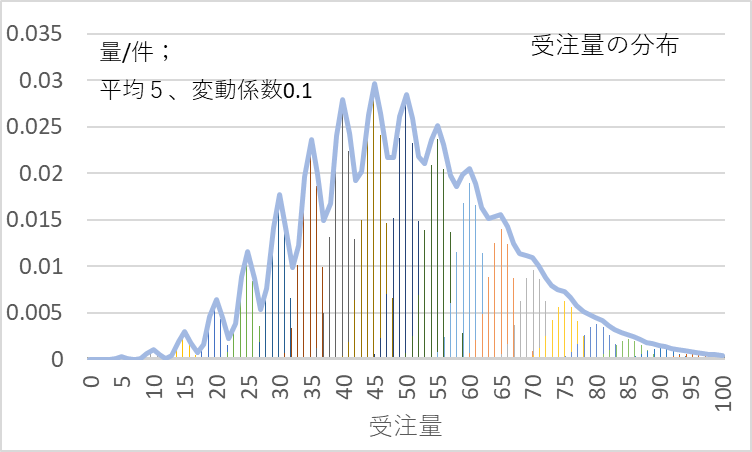
図４　量/件の平均５、変動係数0.1のときの受注量の分布

変動係数を0.2とした時の受注量の分布の一例を図５に示します。変動係数が0.1のときはデコボコしていましたが、変動係数が0.2ではデコボコはほとんど目立たなくなり、正規分布に近似してきます。

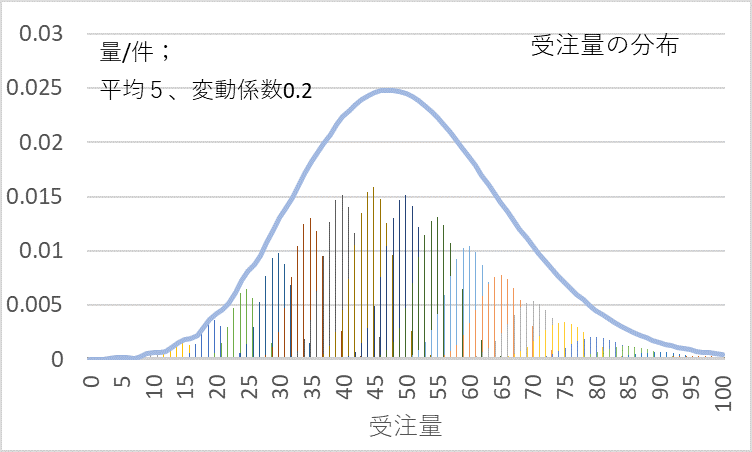
図５　量/件の平均５、変動係数0.2のときの受注量の分布

受注件数、量/件、受注量の関係をまとめると図６のようになります。ランダムに到着する注文は指数分布を使います。ある観測時間間隔で注文件数をカウントすると、その分布はポアッソン分布することが知られています。一方、量/件は1以上の整数であること、適用範囲がひろいことなどの理由でガンマ分布を使ってみました。受注件数が1件の場合、受注量の分布は量/件のガンマ分布そのものになります。受注件数が2件の場合はガンマ分布の任意の2つのデータの和の分布になります。受注件数が3件では任意の3つのデータの和の分布となります。以下同様です。各受注件数ごとの分布を重ね合わせると、受注量の分布を求めることができます。

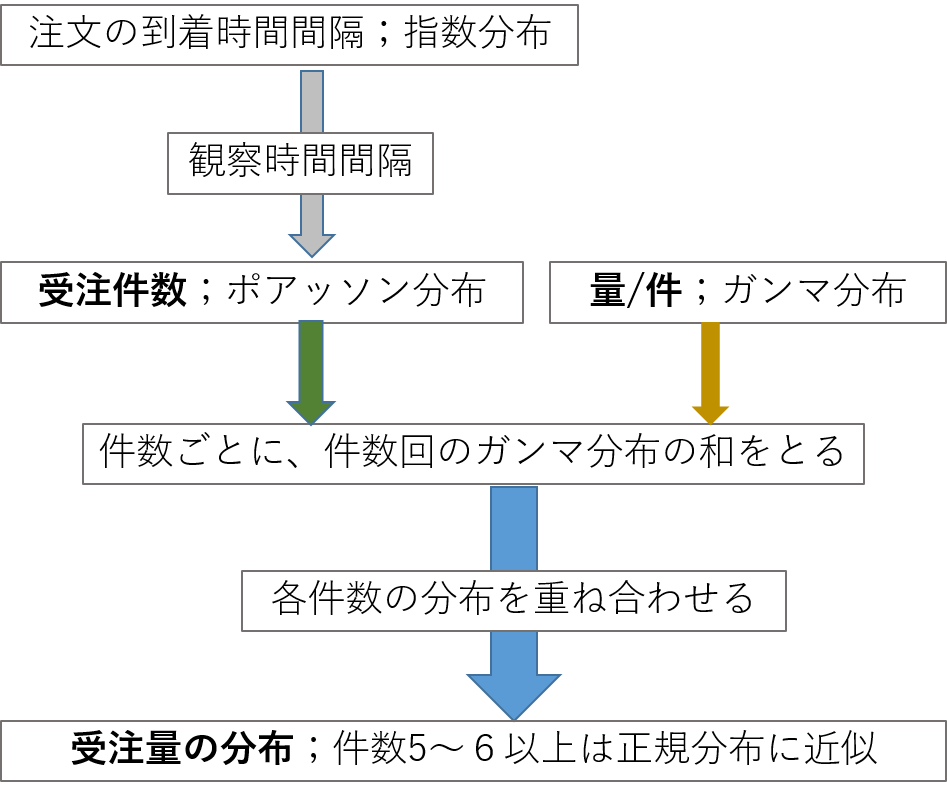
図６　受注件数、量/件、受注量の関係

正規分布は分布の王様と呼ばれることがあるように、最も基本的で、適正在庫を算出するときなど、その他にも様々な分野で利用されています。受注件数が５～６件以上では受注量は正規分布に近似しますので、正規分布の性質を利用することができます。

しかし、受注件数が４～５件以下になると、件数がマイナスにはなりませんので、ゼロが壁のようになり、分布形状も壁で押しつぶされたような形になります（図１参照）。そうしますと、受注量の分布も正規分布ではなくなり、適正在庫の計算など、正規分布に近似することでできた計算ができなくなってしまいます。どうすればいいでしょうか。次回検討することにしましょう。