No.77　リードタイムの変動を扱えない現代在庫管理論の未熟さ

在庫管理では、適正在庫がどのぐらいかが常に話題の中心です。それを決める最も重要な要素が納入（調達）リードタイム。在庫管理側からみれば、納入リードタイムが長くなれば適正在庫量は多くなりますので、できるだけ短い方が望ましい。バラツキも小さい方がいい。そして、納期遵守率も重要ですね。90％以上あればいい方ですが、ダメなところは60％以下なんていうところもあります。納期を遵守するためには納入リードタイムのコントロールが重要です。

在庫管理上避けては通れない納入リードタイム。それが常に一定であれば適正在庫量の算定も比較的正確にできます。が、現実は、そうではありません。バラツキます。納入リードタイムが変動すれば、適正在庫量も多くなることは直観的に分かります。では、どのぐらい多くなるのか。例えば、納入リードタイムの平均が10日、標準偏差2日でバラツク時、同レベルの欠品率を維持するとして、バラツキがない時に対して適正在庫量をどのぐらい増やさなければならないか、簡単に計算できるでしょうか。

納入リードタイムの変動問題。現在どのような策があるのか、調べてみました。納入リードタイムそのものについての説明はたくさんあるのですが、変動についての言及はあまりありません。数少ない、いくつかの説明をまとめますと、
「バラツキを加味して、納入リードタイムの最大値をとる」
ということのようです。式で書くと、

（LT；リードタイム）

納入リードタイムの代わりに最大納入リードタイムを使って、安全在庫は次のような式になるようです。

この式の中に、安全係数が2か所に出てきます。納入リードタイムのバラツキに対する安全係数と需要のバラツキに対する安全係数と。どちらも同じでいいんでしょうかね。安全係数は許容する欠品率との関係で決めるのが一般的ですが、この場合、欠品率と2つの安全係数の関係はどうなるんでしょうか。そんな説明はどこにもありません。安全係数の取り方によってはかなり多めの安全在庫になることもありそうですね。

これが、現在の在庫管理論の現状です。どうみても論理的ではありませんし、実用的でもありません。納入リードタイムの変動をうまく取り扱えていません。なぜなんでしょうね。

実は、この問題、 “No.38　調達リードタイムの変動が受注数量のバラツキに及ぼす影響”と題して以前にも取り上げました。そちらも参考にご覧いただくといいと思います。今回は、前回よりも問題を深く掘り下げ、現代在庫管理論に潜む欠陥を暴きつつ、次代の在庫管理論の再構築を見据え、未来志向的視点を織り交ぜながら、再度取り上げます。

現在の在庫管理論には、いくつかの致命的な瑕疵があります。第1に挙げなければならないのは、需要（受注量、出荷量、、）を捉えるとき、受注件数と1件当りの受注数量（量/件）を識別していないことです。受注件数は来客数、量/件は1人当り買上点数の場合もあります。需要はこの2つの要素で決まるのですが、現在の在庫管理論では、この2つを識別することはまったくありません。

1日、平均10人の客が来て（日によって来客数はバラツキます）、それぞれ1個ずつ買っていく場合と、平均1人の客が来て10個買っていく場合とで、同じ欠品率を維持するための在庫は同じでいいのか、を考えてみるといいと思います。需要はどちらも平均10個ですが、直観的には、１人で10個買う客が来る方が欠品はしやすいのではないか、と感じる方が多いのではないでしょうか。現代在庫管理論ではこれをうまく説明できないんです。来客数と１人当り買上点数を識別していないからです。

受注件数と量/件を識別しないとなぜ、ダメなのか、ですが、時間軸に対する特性が受注件数と量/件では異なるからです。例えば、1日平均10人の客が来る場合、2日間では平均20人、3日間では平均30人、、となりますが、1人当り買上点数はどうでしょうか？　時間軸が2倍になっても3倍になっても、あまり変わらないのではないでしょうか。明らかに、来客数と買上点数は異なった特性を持っていることが分かります。

来客数10人、1人当り買上点数1個の場合も来客数1人、買上点数10個の場合も「1日10個の需要」と認識するのが現在の在庫管理論です。「現代在庫管理論は大雑把かもしれないが、小異にこだわらない方が分かりやすいのでは」、と流す方も多いようですが、これって、現代在庫管理論の根幹にかかわる致命的欠陥なんです。

受注件数と量/件を識別すればいい、というのは簡単ですが、実は、そう簡単ではありません。現代在庫管理論では受注件数と量/件を識別しておりませんので、適正在庫を算出する式、考え方など、そのまま使えなくなってしまいます。新たな在庫管理論を再構築しなければならないことを意味します。これって、大変ですよね、、。でも、現在の在庫管理論が全部ダメ、ということではありません。そのまま使えるところも結構あるんです。どこが使えて、どこを修正しなければならないか、という視点でみれば冷静に対応できるのではないかと思います。

在庫管理論で最も重要なことは、ある時間での需要（受注量、出荷量、、）をできるだけ正確に捉えること。例えば、1日平均10個、標準偏差2個でほぼ正規分布でバラツく、という具合に。適正在庫を求めるときは、補充時間(納入リードタイム＋発注まとめ時間;定期、定量等）での需要の最大値を、欠品率等を考慮して求めることになります。

では、受注件数と量/件を識別した時のある時間での需要量を求める式はどうなるでしょうか。先ず基本要素は次のようになります。

* 受注量；D、、分散＝Vｄ
* 受注間隔；Ti
* 納入リードタイム；T
* 受注１件当たりの受注量（量/件）；Q、、分散＝Vq
* Tでの受注件数；N (N=T/Ti の整数)、、分散＝Vn

納入リードタイムが一定のとき、その間の需要の平均とその分散は次のようになります。

　----式（1-1）

　----式（1-2）

ここでは、出荷時に出荷した数量を直ちに補充発注することを条件にしますので、補充時間＝納入リードタイム　としています。

適正在庫量は次のようになります。

----式（1-3）　　（α；安全係数）

この式の算出過程の詳細につきましては、「STIC発注方式」をご参照ください。

式（1-1）～式(1-3)は納入リードタイムが固定のときです。納入リードタイムが変動したらどうなるかを考えてみましょう。考えやすくするために、量/件は1、受注間隔を一定として、変動するのは納入リードタイムだけとします。式（1-1）と式（1-2）は、Q=1、Vq=0 ですから、

となります。つまり、納入リードタイム；Tでの需要は受注件数のみで決まることになります。先に申し上げましたように、時間軸に対して、受注件数は比例的に増減するのに対して、量/件はほとんど変化しませんので、受注件数だけに注目すればいい、ということです。

あまりにも簡単な式になりました。ここで思考が停止してしまいそうです。でも、ここでやめたら、何も起こりません。よ～く、見てみましょう。受注件数のバラツキ；Vnを。受注件数Nは、N=T⁄Ti ですので、Tiの変動とTの変動の影響を受けます。これは、2つの確率変数の除算の分散はどうなるか、という問題になります。数学的に解く方法はあるようですが、すごく難解なんです。ここでは、TとTiは独立である、と仮定してみます。Tiは市場（顧客）、納入リードタイムは納入業者で決まりますので、両者に明示的な関係はないと考えていいのではないか、と思います。

そこで、Tが変動することによる受注件数Nの分散をV[Nt]、受注間隔が変動することによるNの分散をV[Nti]として、Nの分散V[N]は分散の加法性が成り立つと考えて、

V[N]＝V[Nti]+V[Nt]

となります。ここで注目するのは、Tが変動することによる受注件数Nの分散；V[Nt]です。

Nは次のように表されます。

Tiが一定で定数であれば、1/Tiも定数となります。確率変数の分散公式、 （a；定数、X；確率変数、[X]；Xの分散）から、V[Nt]は、

------式（1-4）

となります。V[T]は納入リードタイムTの分散です。これは、Tの分散;V[T]とそれによる受注件数Nの分散；V[Nt]は比例関係にある、ということを意味します。Tの分散とNの分散の関係を変動係数の視点からみてみます。変動係数とは、

です。Tの変動係数をCｔ、Tの変動によるNの変動係数をCntとすると、Ct、Cntはそれぞれ、次のようになります。

　------式（1-5）

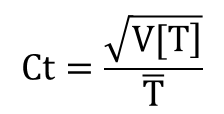　　　　 -------式（1-6）

式（1-4）から、

となりますので、式（1-5）は次のようになります。

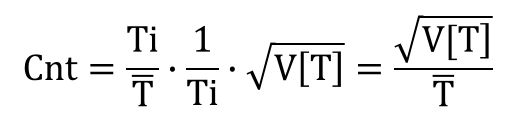
式（1-6）から、

Cnt=Ct

となります。

Tの変動によるNの分散V[Nt]は、式（1-4）と式（1-6）より次のようになります。

納入リードタイムの変動による受注件数の分散を求めるとき、直接関係する変動係数は受注件数の変動係数Cntです。Cntのデータをとるためには納入リードタイムの変動によって増加する受注件数のデータが必要です。しかしこのデータ、簡単には採れません。一方、納入リードタイムのデータは、通常納入日や納入時刻は記録されていますので、その変動係数は簡単に求めることができます。この納入リードタイムの変動係数を受注件数の変動係数として使うことができる、ということになります。

V[Nt]をVnt、V[Nti]をVntiと書き換えて、式（1-2）にTの変動による受注件数の分散の増加分を加えると、受注量の分散Vdは、

　------式（1-7）

となります。実用的には、

----式（1-8）

が使いやすいのではないかと思います。

いかがでしょうか。現代在庫管理論があぐねいている納入リードタイムの変動問題。適正在庫の増加量を算出する分散式を式（1-7）や式（1-8）のようにまとめることができました。納入リードタイムの変動係数の二乗に受注件数の平均の二乗をかけた分だけ、受注件数の分散が大きくなる、ということになります。簡単で、スッキリしました。常識にも合っているのではないでしょうか。

こんな簡単な答えに、現代在庫管理論がたどり着けないのはなぜでしょうか。現代在庫管理論では、受注件数（来客数）と1件当りの受注量（1人当り買上点数）の識別をしていないために、在庫―受注―出荷―補充発注―入庫という在庫管理の循環メカニズムを正しく捉えることができないからです。このことが、実は、納入リードタイムの変動を正しく適正在庫に反映させることができないばかりではなく、在庫管理論をいたるところで歪め、不毛な議論や首をかしげる珍論奇論が氾濫する元凶になっているのではないか、と申し上げたいのです。

尚、ここでは数式モデルで説明しましたが、離散型シミュレータ―でも同じ結果が得られたことを付け加えておきます。