No.75　[書評] 最も変化対応力の強い「不定期不定量発注法」

A書の説明によれば、

―在庫量を移動平均で計算した「1日あたり平均出荷量」で割って「出荷対応日数」を計算する。「出荷対応日数」は、現在ある在庫が何日分に相当するかを示し、それがリードタイム日数（発注から入庫までの日数）と同じか短くなった時、発注する。これが「不定期不定量発注法」だ、と。「1日あたり平均出荷量」で需要の変動を捉え、「出荷対応日数」がリードタイムに達したとき（必要なとき）、必要な量を補充発注する適時適量発注となる。発注間隔は不定期、発注量も不定量、だから「不定期不定量発注法」となる。―

との説明です。

発注方法のポイントをA書から抜き書きすると、

出荷があるたびに発注点をチェックし、発注点が来ていたら、発注量を計算し、発注する。
①出荷があるたびに、「平均出荷量」を計算しなおす。
②「在庫量÷１日あたり平均出荷量＝出荷対応日数」の計算を行う。
③出荷対応日数とリードタイム日数を比較する。
④出荷対応日数がリードタイム日数と一致または下回ったら発注量を計算する。
⑤発注量は、発注量＝１日あたり平均出荷量×在庫日数　で計算する。「在庫日数」は自ら決める数値。

上記の在庫補充発注手順を眺めると、「日数」という文字がやたらに目に付きます。その他にも「日数」の付く語句が頻繁に出てきます。上記も含めて、列記してみます。

* 1日あたり平均出荷量
* 出荷対応日数
* リードタイム日数
* 在庫日数
* 安全在庫日数
* 出荷日数
* 何日分に相当する在庫
* 1日あたり平均出荷量×在庫日数＝発注量

A書が主張する考え方は、在庫管理の主要な項目を「日数」で捉えることに特徴があります。この考え方を「日数基準」と仮称しておきます。

A書が主張する「不定期不定量発注法」は、需要変動への追従能力を上げるために、一般的な「定量発注点方式」に「日数基準」の考え方を適用した発注方法である、ということができると思います。

「定量発注点方式」＋「日数基準」が最も変化対応力の強い「不定期不定量発注法」になりうるのかどうか、私と著者とのやり取りの一部を再現してみます。

[私の質問と著者からの回答]

＜私の質問＞
「1日あたり平均出荷量」（移動平均値）は標準誤差を含むため、それだけでは「売り行きの変化をつかむ」精度は低くなり、実用的に有効な方法かどうか、疑問が残るのではないか。

＜著者の回答＞
この本では平均値を算出するための範囲10日間として説明しているが、発注量の計算を行う際の「１日あたり平均出荷量」は１年間等の長い期間をとるようにしている。短期間の平均は、年間の平均との差をチェックすることで変化のトレンドを見ることで有効に使えると考えているが、短期のトレンドを、ストレートに毎回の発注に反映させることはしない。

移動平均を求める範囲は数日ではなく、1年程度の長い期間だ、との説明。1年程度の長い期間で移動平均を算出して数日、あるいは数週間の需要の変動を捉えることができますかぁ？　例えば、１～２カ月の間に需要が2倍になったら、たちどころに欠品してしまいます。需要の変動を捉えるために移動平均を使うのだと思っていましたので、この説明には唖然としました。

＜私の質問＞
「移動平均の算出日数は10日程度の短期間ではなく1年程度の長期間である」とのことですね。私の評価も移動平均の算出日数5日としておりましたので、評価条件が違うよ、というご指摘ですね。

では、「1日あたりの平均出荷量」の算出日数を1年程度だとするとどうなるか、検討してみましょう。前回指摘させていただきましたように、母集団の標準偏差をσ、算出日数を365日としますと、σ⁄(√365≅σ⁄19) の標準誤差となります。算出日数が10日のときはσ⁄3.2、5日のときはσ⁄2.2 ですので、365日で計算すれば標準誤差はグーンと小さくなり、「定量発注点方式と変わらないようになる」という主張は理解できます。

しかし、以下の手間暇かけて「発注点チェック」を行った結果、「定量発注点方式と変わらないもの」になるのなら、何のために手間暇をかけるのでしょうか。「発注点まで在庫が減ったら発注する」発注点方式の方がずーっと簡単です。下記の「発注点チェック」の利点はどこにあるんでしょうか？しかし、以下の手間暇かけて「発注点チェック」を行った結果、「定量発注点方式と変わらないもの」になるのなら、何のために手間暇をかけるのでしょうか。「発注点まで在庫が減ったら発注する」発注点方式の方がずーっと簡単です。下記の「発注点チェック」の利点はどこにあるんでしょうか？

出荷があるたびに「発注点チェック」を行う。
①出荷があるたびに、「平均出荷量」を計算しなおす。
②「在庫量÷１日あたり平均出荷量＝出荷対応日数」の計算を行う。
③出荷対応日数とリードタイム日数を比較する。
④出荷対応日数がリードタイム日数と一致または下回ったら発注量を計算する。
⑤発注量は、発注量＝１日あたり平均出荷量×在庫日数　で計算する。「在庫日数」は自ら決める数値。

現実の需要は変動しますし、予測が困難な場合が多くあります。事前にわかる場合は、それに合わせて発注点を調整しておけばいいわけですが、予測できない変動に対してどのように備えておけばいいか、在庫管理では定番の課題です。「1日あたり平均出荷量」の算出日数を1年程度にした場合、需要の変動があるとどのようになるか、シミュレーションで確かめてみます。

図１をご覧ください。出荷数/日が250日目から倍増するという条件で、算出日数を1年程度（シミュレーションでは実働日をイメージして250日とした）の場合と10日にした場合の移動平均の推移を示しています。下の図は200日～300日を拡大したものです。

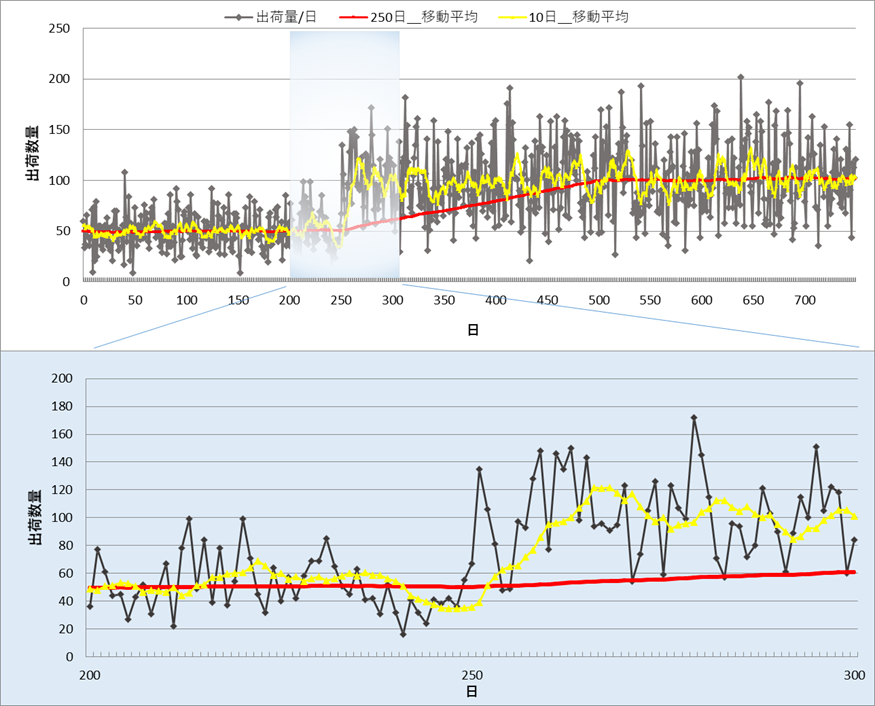
図１　10日間移動平均と250日間移動平均の一例

ご覧のように、250日の移動平均値は時間をかけて徐々に上がっていきます。出荷数が倍増する250日目以降しばらくは、実出荷数と移動平均値の乖離が大きく、つまり、補充発注量と出荷数量との乖離が大きく、間もなく欠品になることを示しています。移動平均の算出日数を長くとればとるほど、変化への反応時間が遅くなってしまうことが要因です。この状態で欠品を防ごうとすれが在庫も大幅に増やさなければならなくなります。

需要が変化する環境下では、致命的な欠陥になるのではないでしょうか。移動平均の算出日数を1年ほどの長い日数をとる理由を、私の疑問点を踏まえて、ご説明いただけると助かります。

“最も変化対応力の強い「不定期不定量発注法」”という謳い文句は、移動平均計算日数が1年程度だ、とすると、「不定期不定量発注法」が最も変化対応力の強い方法であるとは言えなくなるように思います。「不定期不定量発注法」が他の発注方法より優れている点はどんなところにあるのでしょうか？

＜著者の回答＞
平均出荷量の計算対象範囲ですが、長期間販売するものであれば、直近の1シーズン（通年商品であれば１年間）の平均出荷量を利用し、その商品の「実力（＝定常的に売れる量）」を見極めようとしています。
　ここで移動平均と申しておりましたが、上記のように「直近の1シーズン（通年商品であれば１年間）」のデータがたまるまでは出荷があるたびにデータを更新していきますが、一定量のデータがたまれば、そのデータを平均出荷量（実力）とし、ほぼ固定的にその値を使って計算しております。その意味では移動平均と呼ぶ必要はありませんでした。 「実力」に変化がないか監視するため、月に１回程度、年間平均出荷量を計算しなおし、状況に応じ、計算式に反映させる考えです。

著者説明では、移動平均ではなく、1年程度の期間の平均値を固定して使うということだとのこと。これだと、一般の「定量発注点方式」と全く同じになるわけです。「日数基準」はどこにいったんでしょう、、？　著者は「日数基準」の論理的有効性を裏付けることはできず、結局は普通の「定量発注点方式」より勝る利点を示すことはできませんでした。

[シミュレーションによる確認]

No.74で移動平均の特性に付いて調べました。移動平均算出期間を短くすれば反応時間は短くなるが標準誤差が大きくなり、逆に長くすれば標準誤差は小さくなるが反応時間は長くなるというトレードオフがあります。No.74で行いましたシミュレーションデータをみてわかるように、受注量（出荷量）に対する移動平均値の差は、移動平均算出期間全域をみても、実用的な範囲をはるかに超えており、「1日あたり平均出荷量」で売れ行きの変化をつかむことはほぼ不可能です

「定量発注点方式」と「不定期不定量発注法」をシミュレーションで比較してみて、その差をみてみたいと思います。条件は、次の通り。

出荷量（受注量）；平均30個/日、標準偏差12個
納入リードタイム；3日

図2にシミュレーションで使った出荷量データの分布を示します。

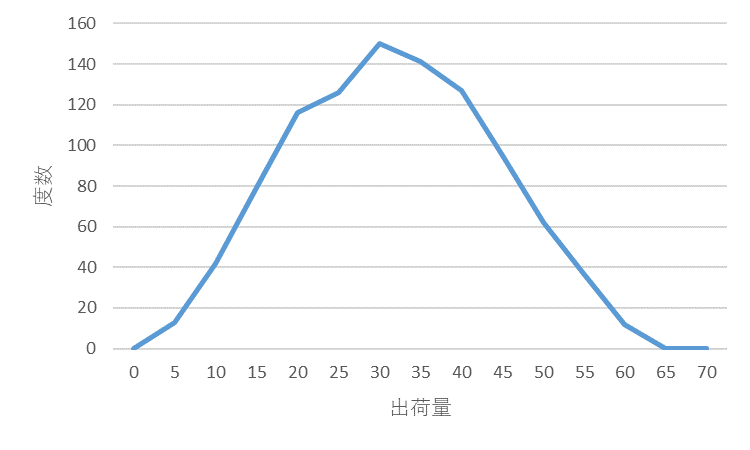
図2　出荷量（受注量）の分布

先ず、定量発注点方式の発注点を計算します。

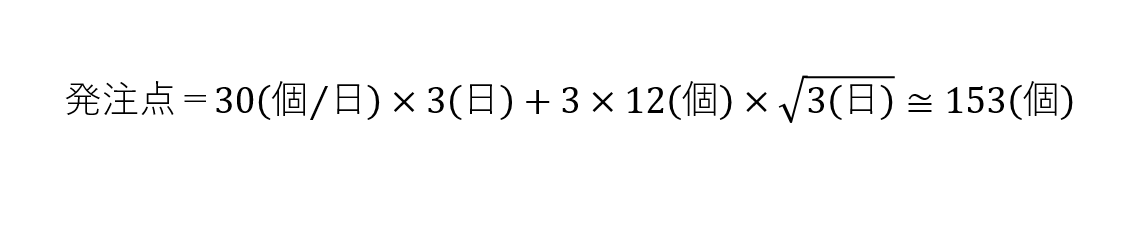
定量発注量；7（日）×30（個/日）＝210（個）とします。
7日としたのは不定期不定量発注の在庫日数と合わせるためです。
シミュレーション時間は1000日。

シミュレーション結果の一例を図3に示します。在庫が発注点（153個）を下回ると一定量（210個）を発注します。発注後、注残状態となり、3日目に入庫され在庫に加わります。

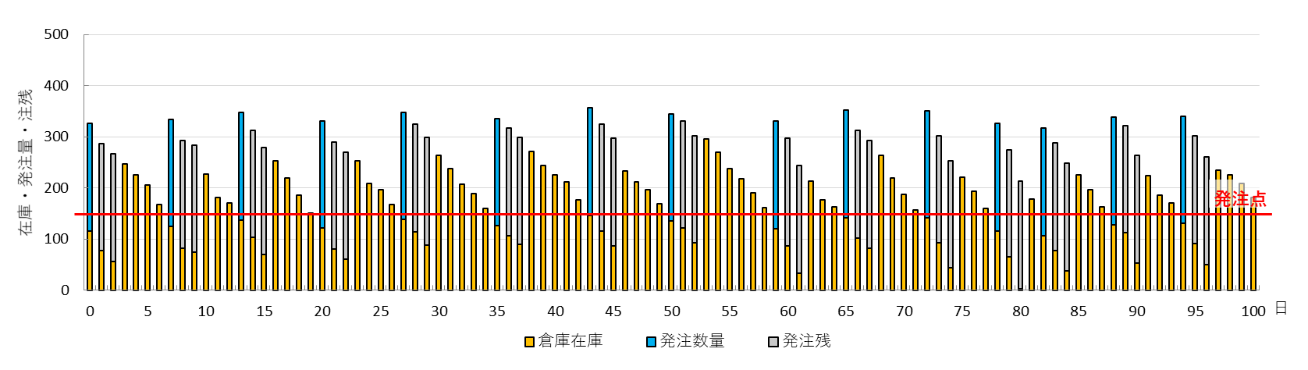
図3　定量発注点方式の在庫、発注量、注残の推移の一例（100日間）

不定期不定量発注法の出荷量（受注量）もまったく同じ。その他の条件は次の通り。
1日あたり平均出荷量；5日間の移動平均値
納入リードタイム；3日
在庫日数；7日
シミュレーション時間；1000日

シミュレーション結果の一例を図4に示します。出荷対応日数がリードタイム日数（3日）以下になると発注量が計算され、発注されます。発注量も発注間隔も変動しているのがわかります。（確かに、不定期不定量発注です）

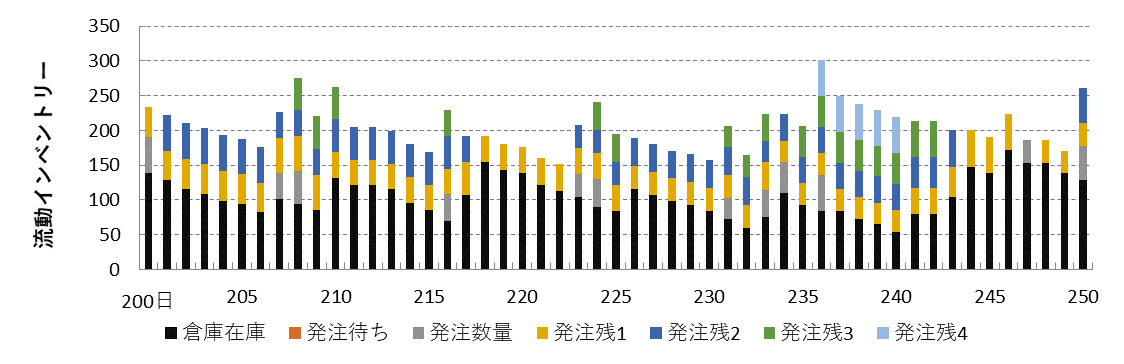
図4 不定期不定量発注法の在庫、発注量、発注残、出荷対応日数の推移の一例（100日間）

表１は定量発注点方式と不定期不定量発注法での倉庫在庫と流動インベントリーのシミュレーションデータをまとめたものです。流動インベントリーとは在庫、発注待ち、発注量、注残を合計したもので、出荷―発注―入庫を循環するインベントリーの大きさを捉えた数値です。

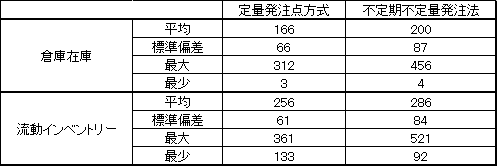
表１　両方式の倉庫在庫と流動インベントリーの比較

図5に両者の在庫量の分布状態を示します。不定期不定量発注法の在庫量の分布が広がっているのがわかります。

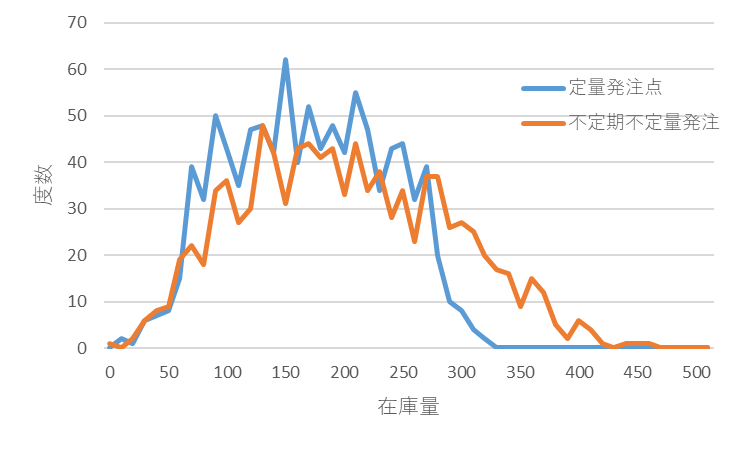
図5　両者の在庫量の分布状態

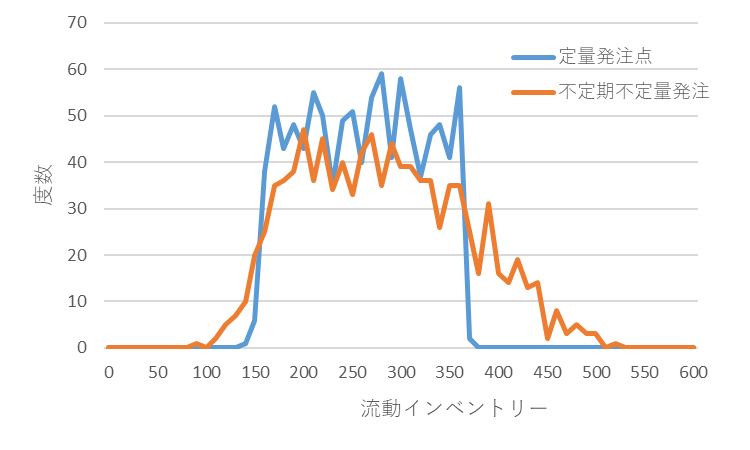
図6　両者の流動インベントリーの分布状態

一般の「定量発注点方式」では、在庫量が発注点まで減少したら発注するという簡単さに比べ、A書の主張する「不定期不定量発注法」の手順は煩雑です。複雑な手順は需要追従能力の向上には全く寄与せず、無用なバラツキを増大させるだけです。その結果、一般の「定量発注点方式」より多くの在庫を必要とすることになり、『「不定期不定量発注法」は最も変化対応力が強い』という説明は成り立たないことになります。