No.74　[書評] 「1日あたり平均出荷量」で売れ行きの変化をつかむ

A書（取り上げた在庫管理の本）の核心部分に迫ってきました。在庫管理の関心事の一つは、変動する需要にいかに追従するか、でしょう。需要の増減によって保持する在庫量が変化しますので、需要を正確に捉え、その量に合った在庫量を保持しなければなりません。在庫管理が抱える、基本的、根本的課題でもあります。

この課題に直接関連するのが、「どのようにして、売れ行きの変化をつかむか」。それを実現する方法として、A書は「1日あたり平均出荷量」をみれば分かる、と言ってるんです。で、今回は、「1日あたり平均出荷量」で売れ行きの変化をつかむことができるのかどうか、調べてみたいと思います。

A書では、「1日あたり平均出荷量」というのは、“移動平均値”だと言っています。例えば、〇月1日；10個、2日；５個、3日；6個、4日；11個の出荷があれば、4日間の平均は8個。5日の出荷が4個なら、直近の4日間の平均は6.5、、、となり、毎日直近の4日間で平均が計算されます。この移動平均で売れ行きの変化をつかむことができるのだ、と。

移動平均を計算するときの日数をｎとして、それを “n日移動平均”と呼ぶことにします。“n日移動平均”とはどんな性質があるか、調べてみます。

受注量（出荷量）の条件を次のようにします。
1日あたり平均受注件数；10件、標準偏差；3.16件
1件あたり平均受注量；5個、標準偏差；2個
ｎ日は、2日、4日、10日、30日の4種類

シミュレーション結果の一例を図１に示します。ｎが大きくなるに従い変化の幅が小さくなります。

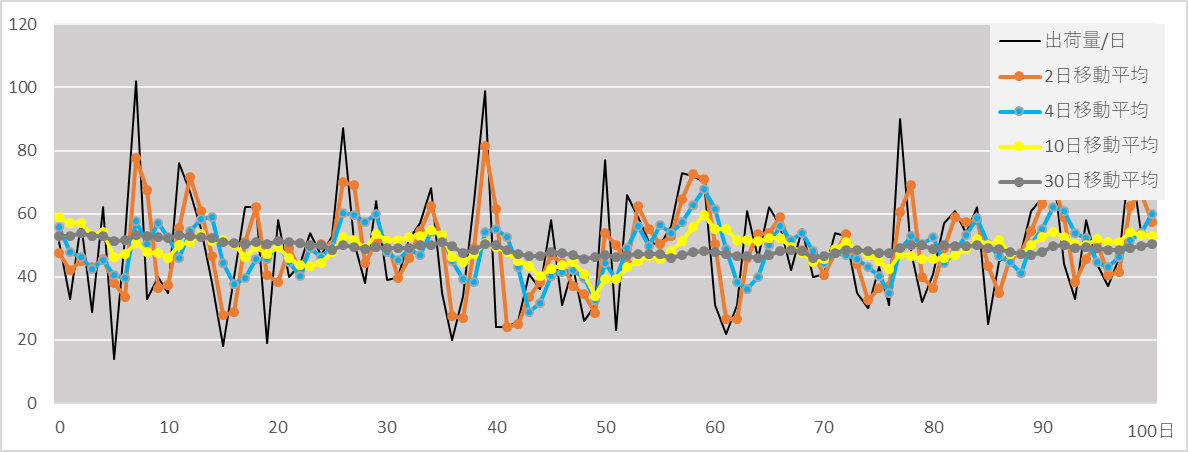
図1 出荷量と移動平均の推移

次に、途中から、1件あたり平均受注量が5個から10個に、標準偏差が2個から3個に増えた場合、受注量と移動平均がどうなるか、その推移の一例を図２に示します。受注量が増えたのは50日目ですので、ｎが大きくなるに従い反応が遅れるようになります。

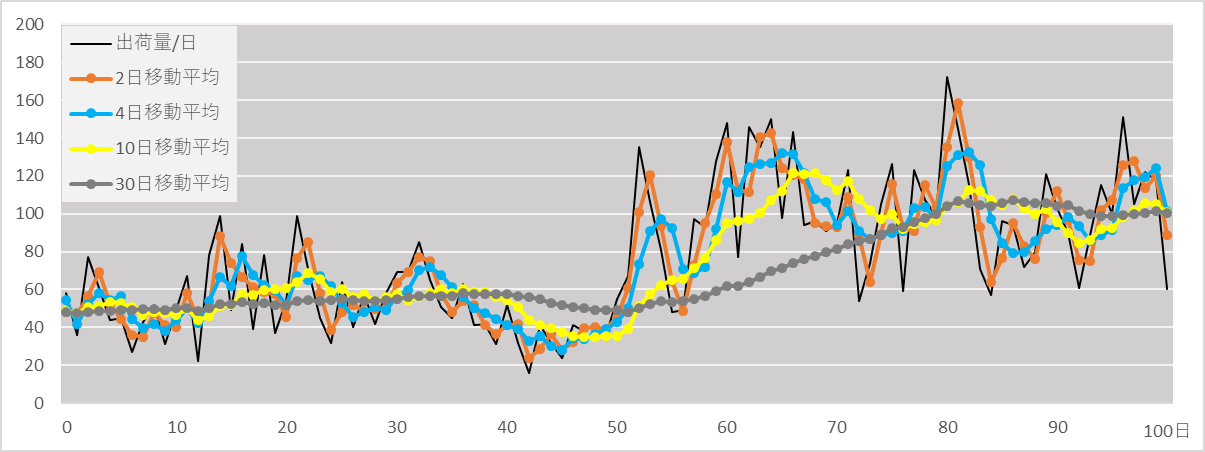
図２ 出荷量が増えたときの受注量と移動平均の推移

図１と図２から分かるように移動平均算出の日数ｎが少なければ反応時間は短くなるが移動平均値のバラツキ幅は大きくなり、逆にｎが大きくなれば移動平均値のバラツキは小さいが反応時間が長くなるというトレードオフがあることがわかります。

ｎとバラツキの関係をもう少し詳しくみてみます。その一例を図３に示します。このようなバラツキを標準誤差とかサンプリング誤差と言っています。ｎが大きくなれば標準誤差は小さくなります。ｎと標準誤差の関係は、受注量の母集団の標準偏差をσとして、次の式で求められます。

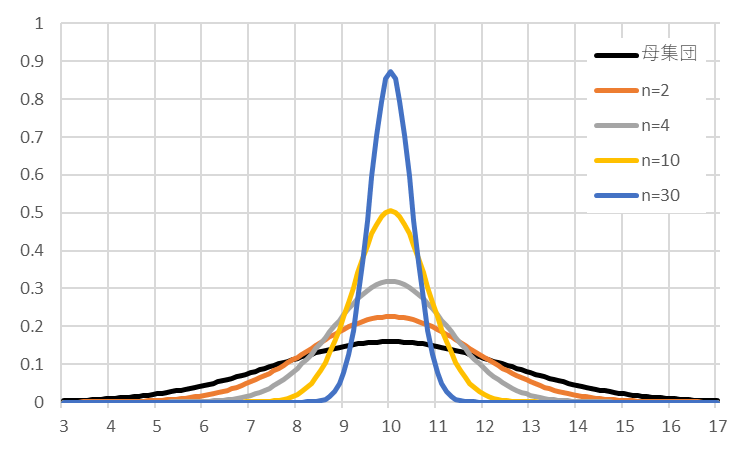
図３　標準誤差の比較

図４は標準誤差とｎの関係を示しています。ｎが5～6ぐらいまでは標準誤差が急激に小さくなりますが、それ以降の変化は緩やかになります。直観的にはｎが４～６ぐらいが標準誤差と反応時間のトレードオフ・ポイントとしていいのではないかと思われます。

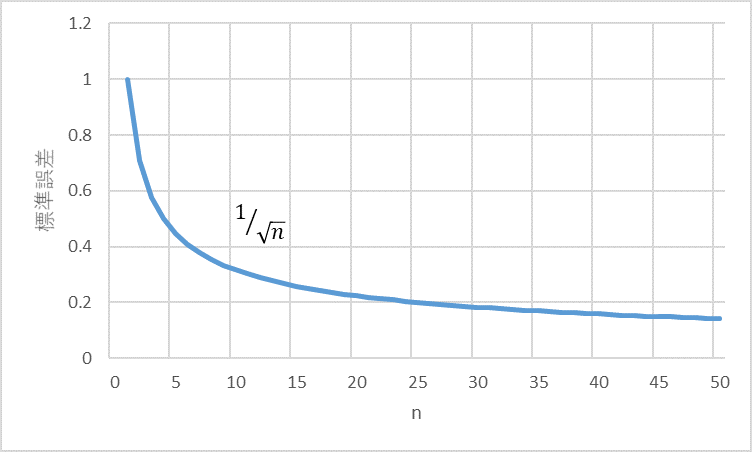
図４　移動平均日数nと標準誤差1⁄√nの関係

「1日あたり平均出荷量」で売れ行きの変化をつかむとは、「売れ行き」を出荷量/日と解して、移動平均値でどの程度、出荷量/日がわかるかということになります。確認してみましょう。図５は出荷量/日と移動平均値の相関を示しています。例えば、移動平均値が50ぐらいのとき出荷量/日は20～100程度の幅がありますので、移動平均値つまり「1日あたり平均出荷量」で売れ行きをつかむことは、実用的に難しいのではないかと思われます。

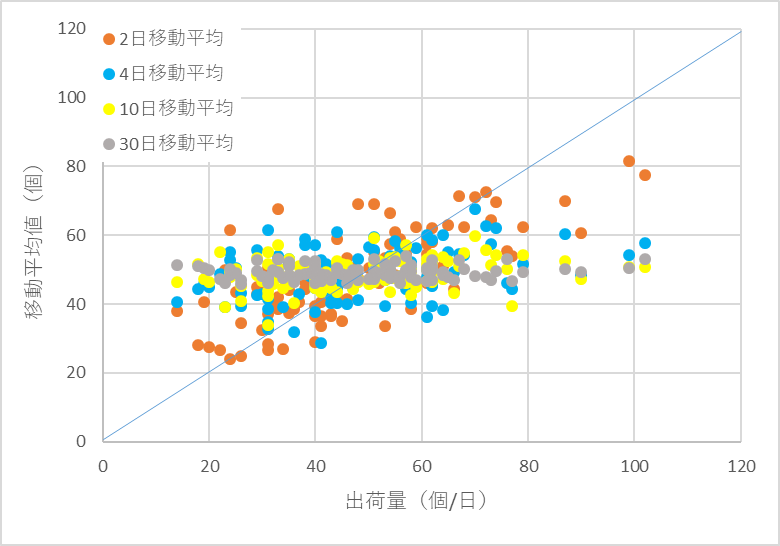
図５　出荷量/日と移動平均値の相関（図１のデータ使用）

図６は需要が変化した時ですが、一見相関は良くなったようにみえますが、この図からも移動平均から出荷量/日を捉えるのは難しいものと思われます。

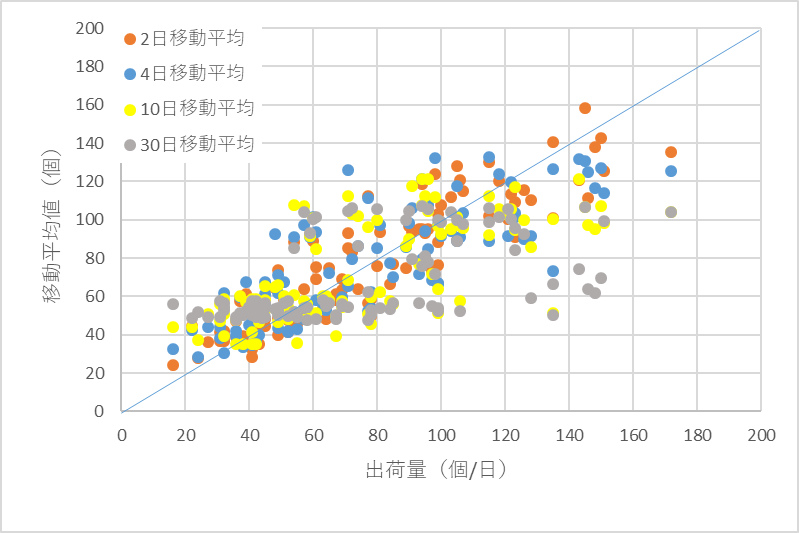
図６　出荷量/日と移動平均値の相関（図２のデータ使用）

「1日あたり平均出荷量」で売れ行きの変化をつかむことができるのか、シミュレーション結果から導き出される結論は、次のようになるのではないでしょうか。

“移動平均で算出された「「1日あたり平均出荷量」で売れ行きの変化をつかむ方法は、標準誤差と反応時間のトレードオフが存在し、実用上有効な最適領域（トレードオフポイント）は存在しない。従って、実用的に「「1日あたり平均出荷量」で売れ行きの変化をつかむことはできない。”