No.73　[書評]出荷がない日は「平均出荷量」の計算対象から除く

いよいよ、まな板に載せたA書の根幹部分に近づいてきました。それは、（赤字部分はA書からの転記）

「1日あたり平均出荷量」で売れ行きの変化をつかむ

です。が、その前に、説明の中で出てくる、

出荷がない日は「平均出荷量」の計算対象から除く

という記述について検証してみたいと思います。

表題の「平均出荷量」とは「1日あたり平均出荷量」のことです。「1日あたり平均出荷量」は移動平均値である、と言っています。移動平均とは、例えばX月6日の平均出荷量は、X月1日、2日、3日、4日、5日の出荷量の平均をとり、X月７日の平均出荷量は2日、3日、4日、5日、6日の平均をとる、ということです。A書の説明をみてみましょう。

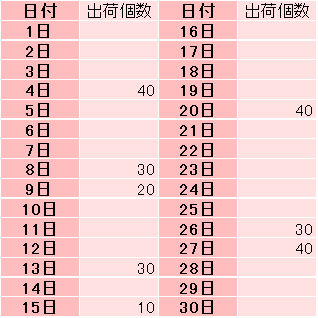
表１　ある商品の1ゕ月の出荷量

A書では、表１のような出荷パターンのときはどうするか、次のように説明しています。

このような、出荷が毎日あるとは限らないという商品はたくさんあります。この商品の月間出荷量は240個。出荷がない日も計算対象に含めたカレンダー日数で計算する場合、平均出荷量の計算式は下記のようになります。

240個÷30日＝8個

1日あたり平均出荷量は「8個」という計算です。しかし、実際の出荷状況を見れば、出荷があるときは10個の倍数で出ています。もし、「必要最小限の在庫＝1日分の在庫」と決めて運用したらどうでしょう。8個の在庫しか持っていないのですから、顧客の「10個」の注文に応えられません。毎回、欠品になってしまいます。そんなことにならないように、出荷の実態を踏まえて運用すべきルールが「出荷のない日は除いて1日あたり平均出荷量を計算する」なのです。

計算は、実際の出荷のあった「8日」を用いて平均を出します。

240個÷8日＝30個

つまり、平均出荷量は8個ではなくて、30個だというわけです。5日分の在庫を持った場合の例として表２を挙げています。平均出荷量が8個だと2回の欠品が出るが、30個だと欠品は起きない、と説明しています。

表２　5日分の在庫を持った場合

このA書の説明、みなさまはどう思いましたか。納得された方もいれば、そうでない方もいらっしゃるのではないかと思います。

すぐに、出そうな質問が、「なんで5日分なんですか？」ではないでしょうか。「3日分でも欠品はでませんよ」と言いたくなります。在庫管理は欠品率が同じなら在庫を最少にすることを狙いますが、３日分でも欠品が出ないのに、なんで5日分の在庫が必要なんですか、という疑問は当然ですね。

では、百歩譲って、5日分の在庫を持つことを良しとしましょう。その時、「欠品率は何％になるんですか？」という問いには答えてほしいですね。もちろん、統計的誤差はあってもかまいません。これに応えられないようだと、在庫管理とは言えなくなるのではないでしょうか。欠品率と在庫量のトレードオフを計算するのは在庫管理のメインテーマのひとつですから。

結論から言いますと、この件（くだり）は、根本的な欠陥を含んでいます。どんな欠陥かと言いますと、出荷（需要）のない日もある需要パターン、一般的に間欠需要パターンと呼んでいますが、のときの需要分布の捉え方に不合理な点があるということです。間欠需要パターンについては、No.67とNo.68に詳しく説明しておりますので、そちらをご参照頂きたいと思います。

ここでは、No.67とNo.68で説明をした方法に沿って、A書の課題を解いてみたいと思います。

先ず、平均出荷件数を求めます。出荷が40個のときもあれば20個のときもありますが、出荷件数はすべて1件とします（もちろん40個の出荷を2件としても問題なく計算できます）。30日間で8件の出荷件数がありますので、

平均出荷件数；N＝8/30≅0.267

となり、その分散は、エクセルで計算して、

出荷件数の分散；Vn≅0.196

1件当りの平均出荷量（量/件）は、8件で240個出荷ですので、

量/件；Q＝240/8=30

その分散を計算しますと、

量/件の分散；Vq=100

となります。

平均出荷量；

出荷量分散；

ここでδは、

なので、出荷量の分散は、

となります。必要在庫量は。安全係数αを3として、次のようになります。

必要在庫量としては64個あればよい、というふうに計算されます。これは在庫補充時間が1日のときですが、それが2日のときは、次のようになります。

平均出荷量；

出荷量の分散；

A書では、在庫量は5日分の150だ、と唐突に出て来ました。欠品は、確かに出なくなりますが、その根拠はどこにあるのか。理論不在の詭弁と言わざるを得ません。

出荷がない日を「平均出荷量」の計算対象から除いてはいけません！！　件数と量/件を識別して計算すればいいのです。