No.68　間欠需要の取り扱い方

前回（No.67）、間欠需要について考えてみました。巷で散見される間欠需要のバラツキ算出方法のポイントは、
①出荷ゼロの日のデータを省く
②出荷率（出荷のある日の割合）で補正
ですが、これは全然、ダメでした。ごく普通に、間欠需要データをそのまま使って平均と標準偏差を求めた方が良い、ということでした。

このような方法が、間欠需要に対する新理論だ、と、得意げに喧伝されているようです。これって、エクセルで簡単に確認できますので、時間のある方は挑戦してみてください。

このような似非理論がまかり通る元凶は、、、現在の在庫管理論に内包する論理的欠陥にあるのではないか、、、。

間欠需要のメカニズムは？　例えば、小売店。店を開け、最初の客が来た。数分後2人目の客が来た。3人目の客が来たのは1時間後。４人目、5人目、、、と来るわけですが、来客の時間間隔はランダム。ランダムな時間間隔で到着する来客数を数えるためには、ある一定の時間間隔内に何人来たかを数えることになります。ある時間間隔（以下、集計時間）を1日（24時間）とすることが多いと思います。そうすると、1日目は25人、2日目は32人、、、というデータが蓄積されます。横軸に来客数、縦軸に回数をとって来客数の度数分布が出来上がります。20人来た日は2回、21人来た日は4回、、、30人来た日は15回、、、50人来た日は3回、、、というふうに、普通は山形の分布で、正規分布に似た分布形状になります。

来客の時間間隔が長くなると、例えば30時間とかになると、客の来ない日も出てきます。これが間欠需要状態です。ところが来客の時間間隔はそのままで、集計時間を短くしても、例えば1日の集計時間を1時間にすると、間欠需要状態となります。つまり、間欠需要状態は来客の時間間隔と集計時間の関係で決まるわけです。1人の客が一度に何個買うかは、売上数量には直接影響しますが、間欠需要状態には影響しません（客は不特定多数という条件で）。

この来客数の分布はポアッソン分布によく合うことが知られています。ポアソン分布は、レジでできる待ち行列、インターネットや電話回線の能力算定など、待ち行列理論ではお馴染みの分布です。

間欠需要を知るには、ポアッソン分布の性質を利用すると分かりやすいのではないかと思います。図１は、前回も載せましたが、ポアッソン分布の1例です。集計時間が1日（24時間）のとき、客の平均到着間隔が24時間なら、来客数の平均は1人。平均到着間隔が12時間なら来客数の平均は2人。平均到着間隔が48時間なら来客数の平均は0.5人。

来客数の平均が0.5人のとき、来客ゼロの日の確率は60%、来客が1人の日の確率は30%、2人来る日の確率は8%、、、。ということがポアッソン分布でわかります。

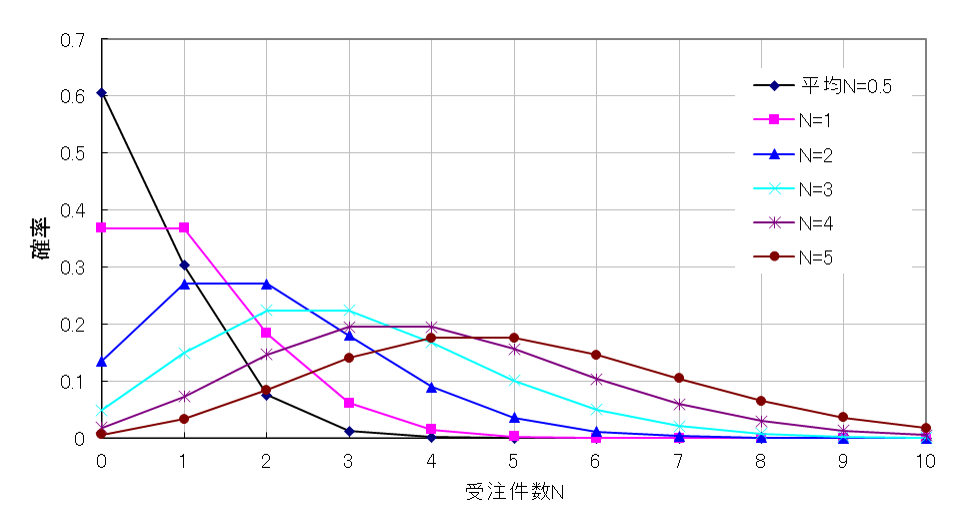
図1　ポアッソン分布の例

ポアッソン分布は横軸がゼロ以上でマイナスはありません。受注件数の平均が小さくなるとゼロで抑えられますので、分布形状が非対称になってきます。データ処理をする場合、平均と標準偏差を求め、分布形状は正規分布と仮定して、サービス率に対する安全在庫などを求めるわけですが、非対称になると正規分布とのズレが大きくなります。

どの程度のズレが生ずるのかの一例を図2に示します。量/件が10、その変動係数が0.2の間欠需要分布と間欠需要データの平均と分散で決まる正規分布との比較です。平均受注件数に対して両者のサービス率の差がどのように変化するのかを示しています。平均受注件数が小さくなると非対称性が顕著になり、差も大きくなることが判ります。差がプラスであることは、正規分布の近似値が大きくなることを示しています。

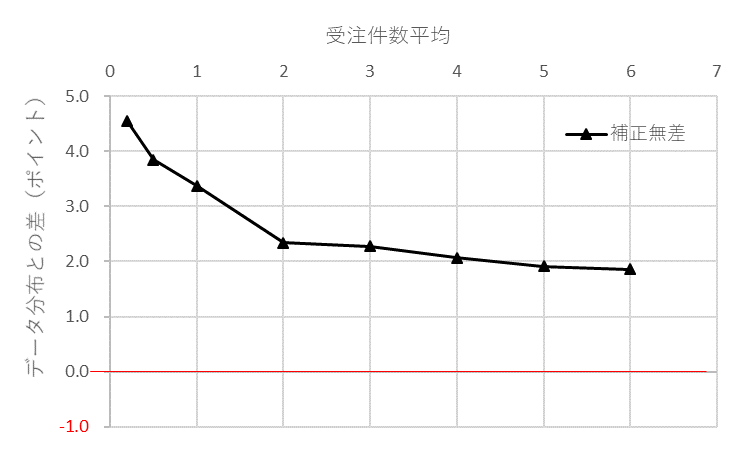
図2 間欠需要と正規分布のサービス率の差

このズレをもう少し小さくできないか。常識的には、図２と同じようなカーブで補正できるんじゃないか、と思われます。導出過程は省略しますが、補正値をδとして、次の式を例示しておきます。は受注件数の平均です。

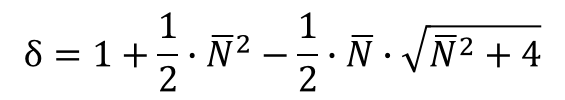
補正値δのカーブは図3のようになります。図2のカーブと似ているでしょ。もっと良い補正カーブがあるかもしれませんので、ここでは1例としておきます。

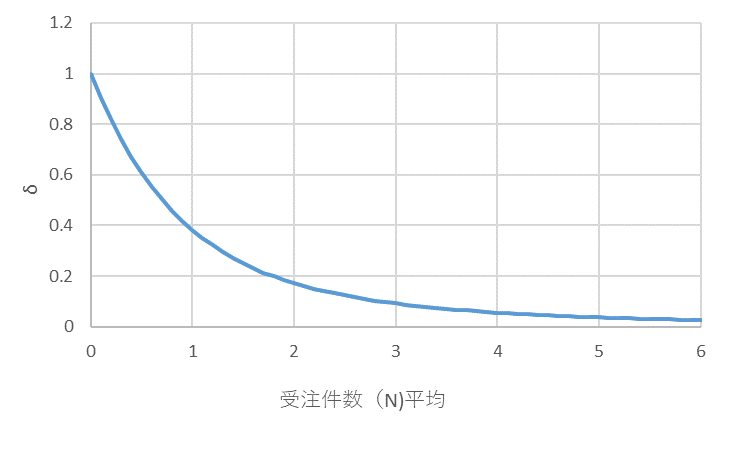
図3 受注件数平均と補正値δの関係

この補正値δで受注件数の分散Vnを次の式で補正します。

受注件数の分散Vnをδ分、大きくするわけです。これは、正規分布と比べると間欠需要の分布のすそ野が広がっているのを補正する、という意図です。受注件数の分散Vnだけを補正します。量/件の分散Vqは間欠需要との直接的な関係がないので、補正はしていません。補正後の差の一例を図4に示します。補正し過ぎの感が多少ありますが、差が小さくなっていることが判ります。

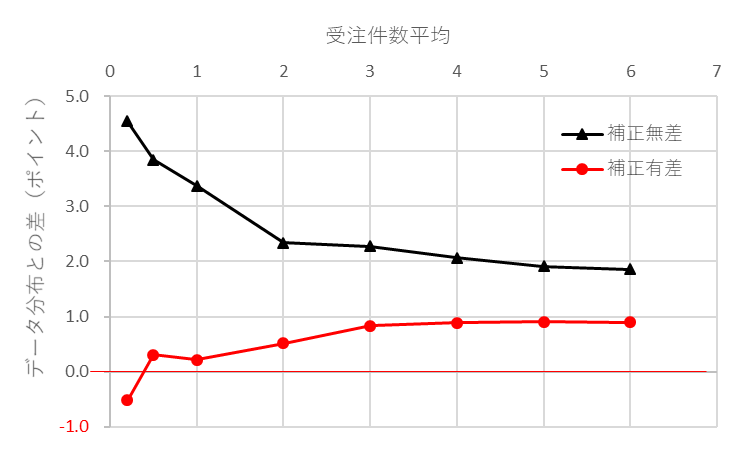
図4　補正後の差

冒頭、現在の在庫管理には論理的欠陥があるのではないか、と申し上げました。顕著な欠陥のひとつは、需要（受注量）を捉えるとき、受注件数と量/件を識別していないことではないか。間欠需要は受注件数の発生メカニズムで説明できますが、巷の在庫管理論では両者を識別しておりませんので、うまく説明できないんだと思います。その結果、①出荷ゼロの日のデータを省く、②出荷率（出荷のある日の割合）で補正、といった、意味不明な新理論が巷を闊歩することにつながっているのではないでしょうか。

前回（No.67）も紹介しましたが、補正の効果の例を再掲しておきます。

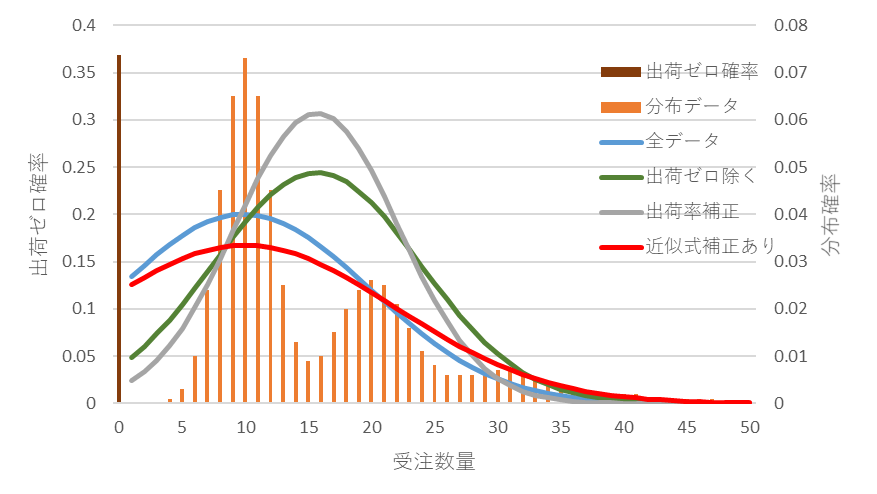
図5 受注件数平均1、補正有の分布（赤）

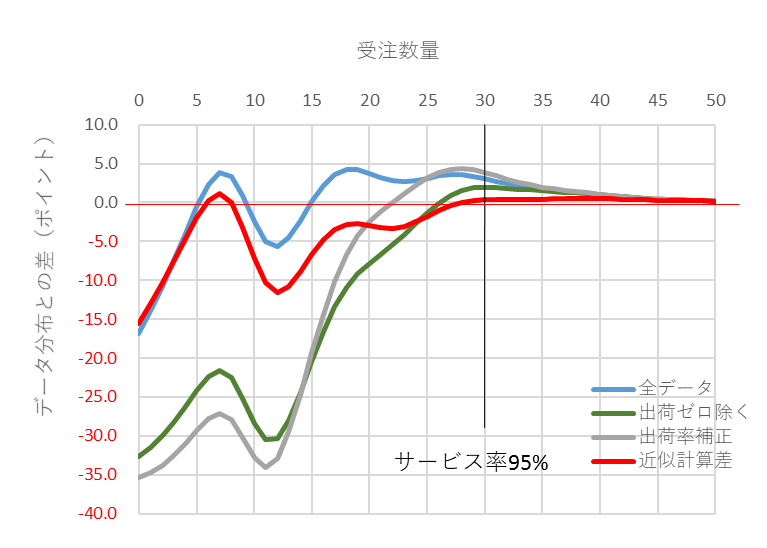
図6　受注件数平均1、補正分布有の差（赤）

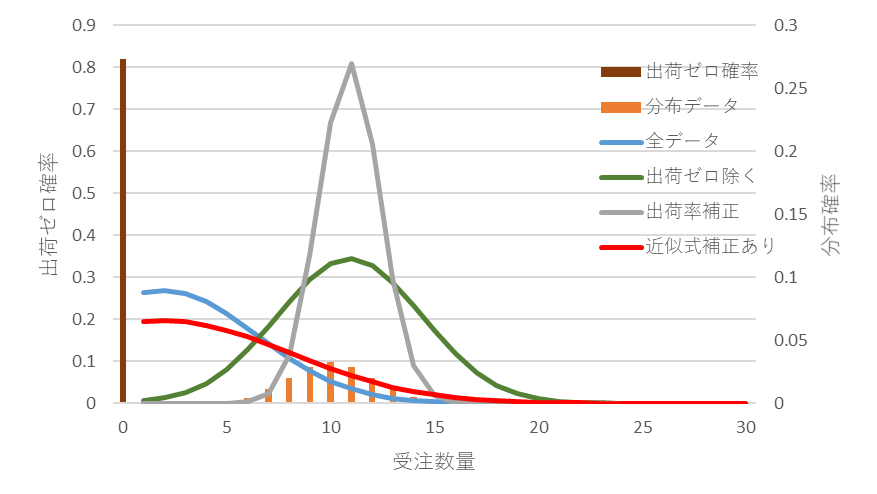
図7　受注件数平均0.2、補正有の分布（赤）

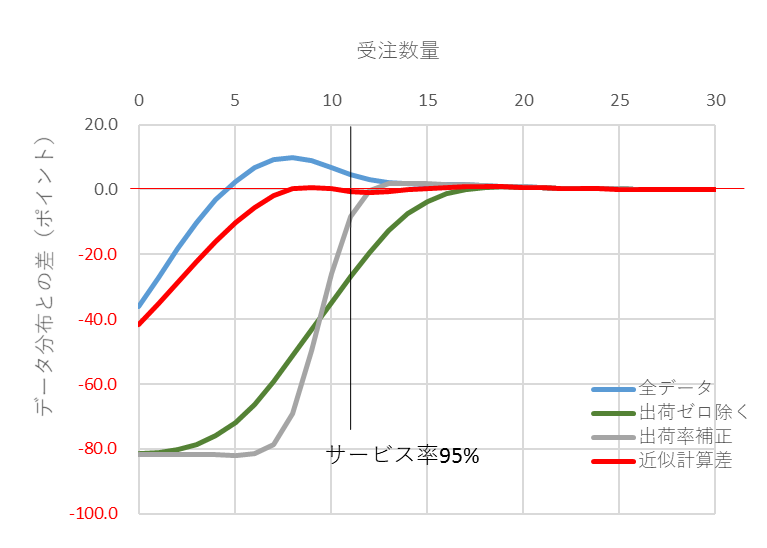
図8　　受注件数平均0.2、補正分布有の差（赤）

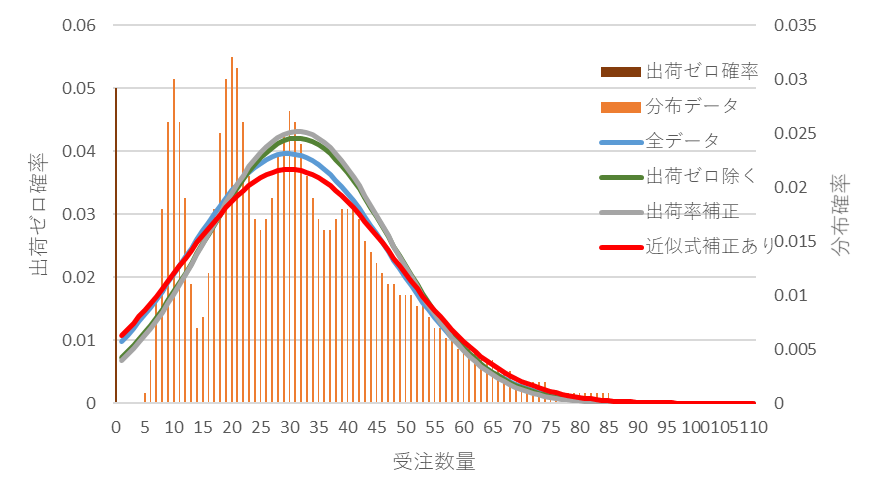
図9　受注件数平均3、補正有の分布（赤）

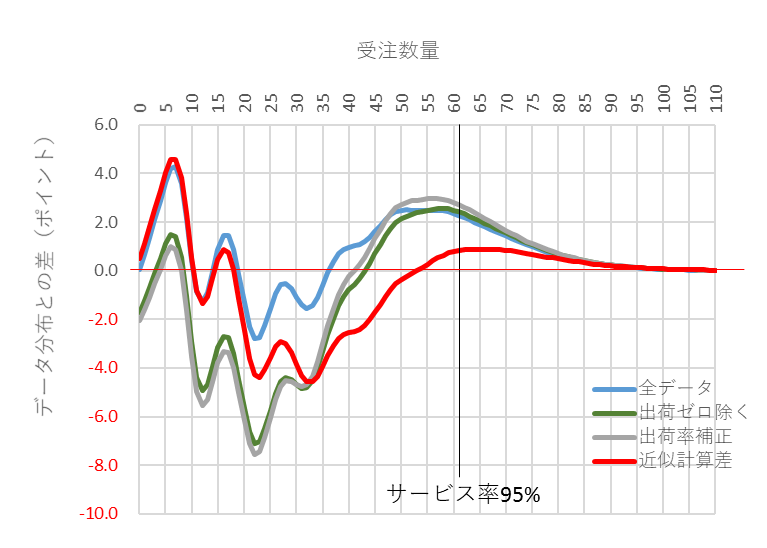
図10　　受注件数平均3、補正分布有の差（赤）