No.67 間欠需要のメカニズム
間欠需要とは、注文がある日もあればない日もあるというような需要パターンです。このような需要パターンは、特殊というよりは、よくあること。でも在庫管理上は、取り扱いに工夫がいるようです。どんなふうに扱われているか、在庫関連の本やWebsiteを調べてみたら、次のような説明が数カ所で見つかりました。
~~~~~~~~~~~~~~~~~~~~~~
・発注点方式の場合 ![]()
出荷率は次のように計算する。
平均、標準偏差の計算は、出荷がゼロであった日のデータをカウントしないで計算する。
~~~~~~~~~~~~~~~~~~~~~~
この説明の特徴は、2点。
①出荷ゼロの日のデータをカウントしないで平均と標準偏差を求める
②出荷率の平方根を①の標準偏差に乗じて補正する
直観的に、これは変だな、って思います。出荷ゼロの日のデータをカウントしない、つまり、ないことにしちゃうって、ちょっと乱暴じゃないの? 出荷数がゼロで、計算しなきゃいけないんじゃないんですかね。
このような私の疑問に応えるような記事は見つからず。前々から、疑問に思っていましたので、ここらへんで、白黒はっきりさせましょう。まぁ、それほど力が入っているわけではありませんが、、。
手始めに、間欠需要の特徴を概観してみましょう。注文がある日もあればない日もある。こんな商品は典型的な間欠需要パターンですね。1回の注文でどれだけの数量の注文が来るかは、後回しにして、注文件数だけに注目します。もう少し詳しくみてみましょう。例えば、1週間(7日間)で注文のある日は、少ないときは1日、多いときは5日だとします。このような注文パターンを1週間単位でみたらどうなるでしょうか。1週の間では注文がない日はなくなります。つまり、1週間単位でみると、間欠需要ではなくなってしまいますね。
間欠需要は、集計時間間隔を長くとると、間欠需要ではなくなるって、ご存知でした? で、これで問題解決? 、、というわけにはゆきません。在庫補充のメカニズムの中で重要なのは、集計時間間隔ではなく、在庫の補充にかかる時間(以下、補充時間)であって、この補充時間は納入業者や運送会社、時には生産ラインのリードタイムなどによりますので、簡単に変えることはできません。ですから、補充時間で間欠需要パターンであるならば、在庫管理側でそれを避けることは、簡単にはできないんです。なので、間欠需要についてまじめに考えてみましょう、というわけ。
間欠需要を説明するのに便利な分布があります。ポアッソン分布(図1参照)って呼ばれています。例えば、注文はランダムに来るとして、1日平均1件の注文が来るとします。この場合、注文がない日(横軸;0)の発生確率は36.8%。1件の注文が来る日(横軸;1)の確率も同じく36.8%。2件の注文が来る日(横軸;2)の確率が18.4%、3件の注文が来る日(横軸;3)の確率が6.1%、、、。図1の平均件数1(ピンク)がその確率を示しています。1日の注文件数の平均が変わると確率分布も変わります。
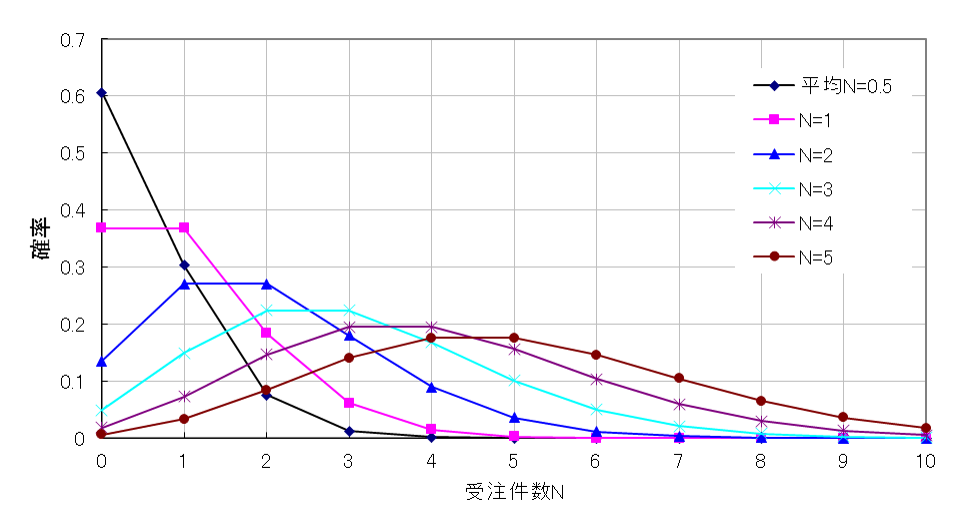
図1 平均受注件数が0.5~5のときの受注件数の発生確率
受注件数は整数しかとりませんので離散型の分布となります。平均件数は整数でも小数でもかまいません。平均受注件数が少なくなるに従い、注文ゼロの日の確率は高くなります。
もうひとつの特徴は、平均受注件数が多くなると、そうですね、4~5以上だと、確率分布形状が正規分布に近似できるということです。ザックリと言えば、平均受注件数が4以上は受注件数ゼロの日の確率も2%以下であり、正規分布として扱っても大きな誤差はでないのではないでしょうか。
問題は、平均受注件数が3以下の場合。分布形状をみても正規分布にはみえません。この辺りをもう少し詳しくみてみたいと思います。
その前に、1回の注文での数量(以下、量/件)を考慮するとどうなるかをみてみます。図2は受注件数平均が1で、量/件の平均が10一定(変動係数;0)のときの受注数量の分布です。0、10、20、、に棒がありますがその間にはありません。受注件数平均1のポアッソン分布と比べると、10倍の位置に棒があることがわかります。1件の受注で10の注文がありますので、このようになります。
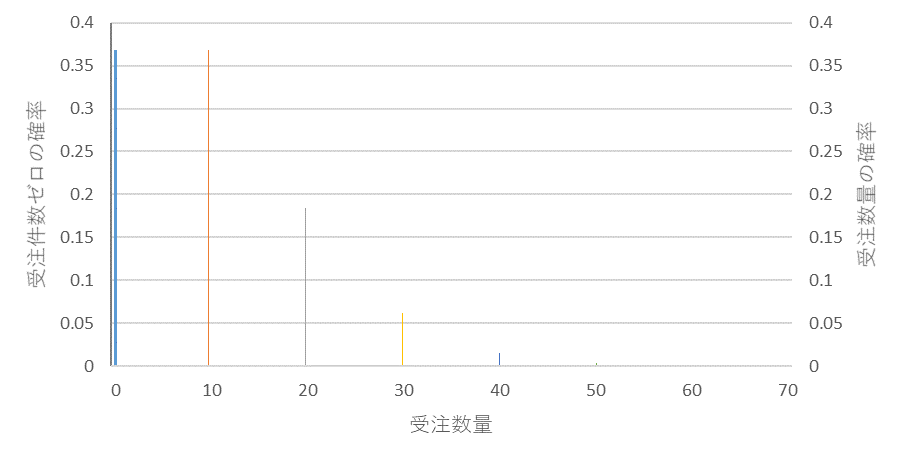
図2 受注件数平均;1、量/件の平均;10、その変動係数:0
図3は量/件の変動係数が0.1の正規分布で変動した場合の受注数量の分布です。10、20、30、、のバラツキが表れてきます。
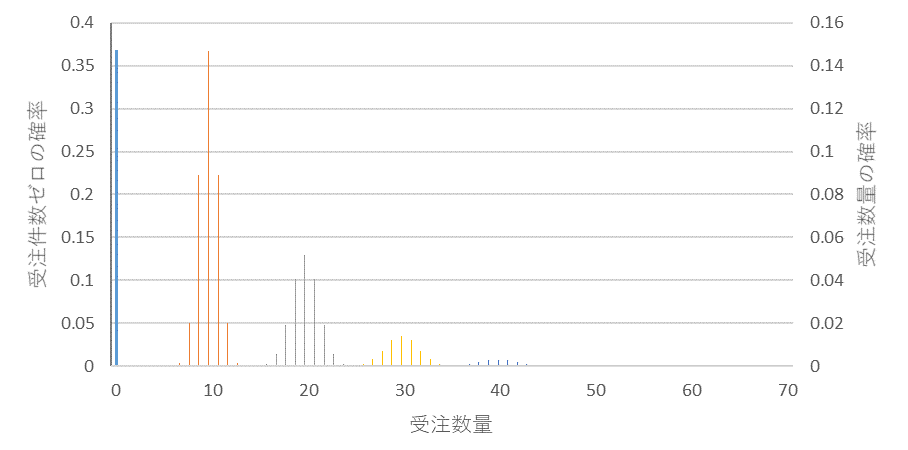
図3 受注件数平均;1、量/件の平均;10、量/件の変動係数:0.1
図4は量/件の変動係数が0.2、図5は0.3のときの受注数量の分布です。図5の曲線はトータルの受注数量の分布です。
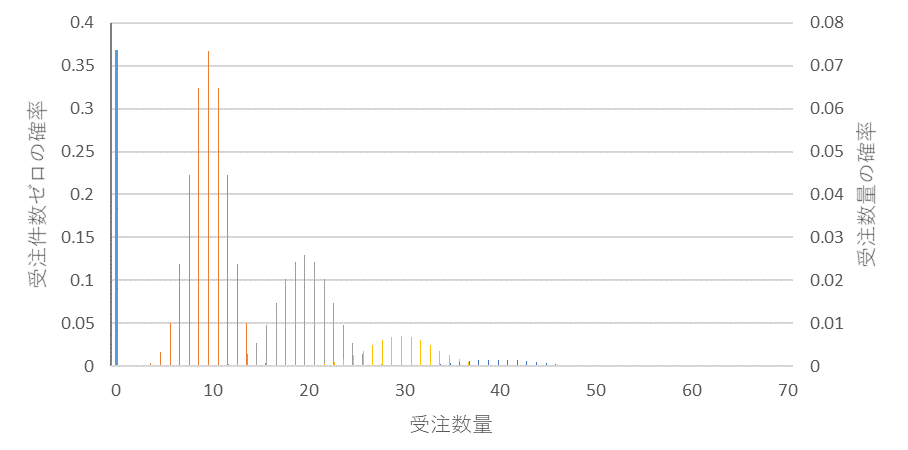
図4 受注件数平均;1、量/件の平均;10、量/件の変動係数:0.2
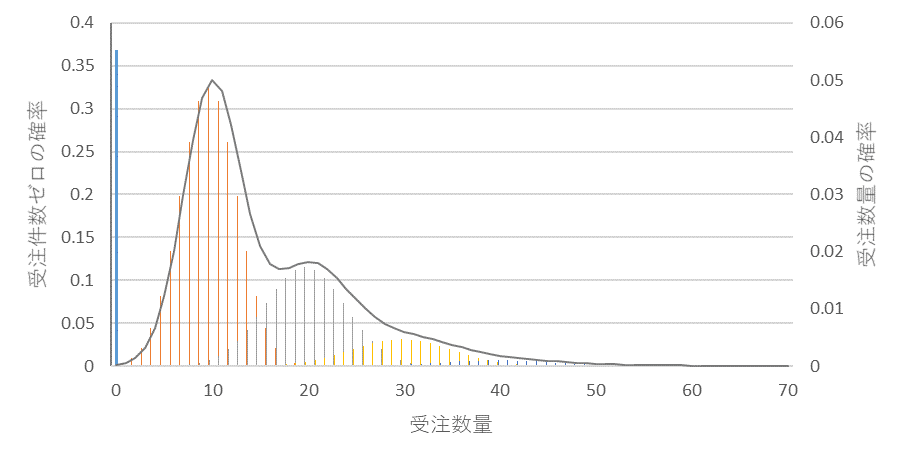
図5 受注件数平均1、量/件の平均;10、量/件の変動係数:0.3、曲線はトータルの確率分布
図2~図5で量/件の変動係数を変化させた結果、受注数量の分布形状は変化しましたが、受注件数0の確率は変わりません。つまり、間欠性は平均受注件数で特徴付けられていることがわかります。図1でもわかりますように、平均受注件数が少なくなるに従い受注件数0の確率が高くなります。表1を参照ください。これをみますと、平均受注件数が3以下のとき、間欠性が高くなることがわかります。

表1 平均受注件数と受注件数0の発生確率の一例
もうひとつみておく必要があるのは分布形状です。図2~図5をみてわかりますように、受注数量の分布形状はでこぼこで、左右対称ではなく、右側にすそ野を引いています。どう見ても正規分布とは異なります。
間欠需要の特徴をまとめますと、
①間欠性は平均受注件数で決まる
①平均受注件数が3以下で間欠性が高くなる
②間欠性が高くなると受注量の分布形状が非対称となり、正規分布近似性は低下する
つまり、間欠需要パターンは平均受注件数3以下で顕著になり、分布形状が正規分布ではなくなるので、そのズレを補正する工夫が必要だ、ということですね。冒頭で挙げた工夫が、本来の間欠需要の分布形状にどの程度近似するのか、つぎの3通りの方法で調べてみたいと思います。
① 出荷ゼロのデータは出荷数をゼロとして、平均と標準偏差を計算する(図表示;全データ)
② 出荷ゼロのデータを省いて、平均と標準偏差を計算する(図表示;出荷ゼロ除く)
③ ②で求めた標準偏差に![]() をかけて標準偏差を求めなおす(図表示;出荷率補正)
をかけて標準偏差を求めなおす(図表示;出荷率補正)
条件は、受注件数平均1、量/件の平均;10、量/件の変動係数:0.2(図4 参照)。
注記)ここで出荷とは、受注がある分を出荷することを言い、実質的には出荷=受注。
図6は、間欠需要のデータを①、②、③の方法で算出した平均と標準偏差で決まる正規分布を重ねたものです。出荷ゼロのデータを除くと2~3山ある間欠需要の受注数量分だけのデータで平均と標準偏差が計算されます。出荷率は間欠需要の場合は1以下になりますので、出荷率で補正すると標準偏差は小さくなります。間欠需要のデータをそのまま使って計算しますと、平均は小さくなり、標準偏差は大きくなります。
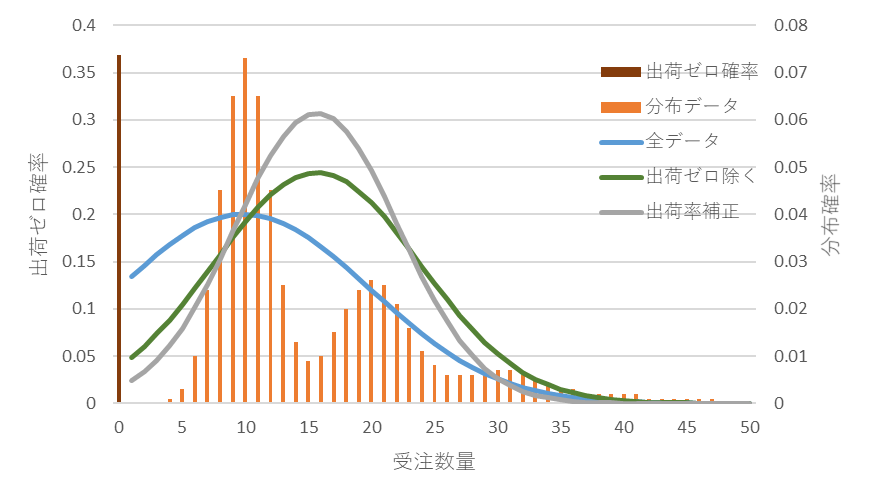
図6 間欠需要の度数分布と①全データ、②出荷ゼロ除く、③出荷率補正の正規分布
間欠需要の分布と①、②、③で計算した平均と標準偏差の正規分布の累積確率(%)差(ポイント)がどの程度あるか、比較した結果の一例を図7に示します。累積確率はサービス率と言い換えることもできます。
在庫管理で使う領域は、一般的には、サービス率95%以上(欠品率5%以下)ぐらいでしょうから、その位置でみるのがいいのではないかと思います。全体をみれば計算方法の違いで差のカーブは異なりますが、サービス率95%の位置でみれば、あまり大きな差はありません。しいて言えば、差の小さい順は、②出荷ゼロ除く、①全データ、③出荷補正の順。
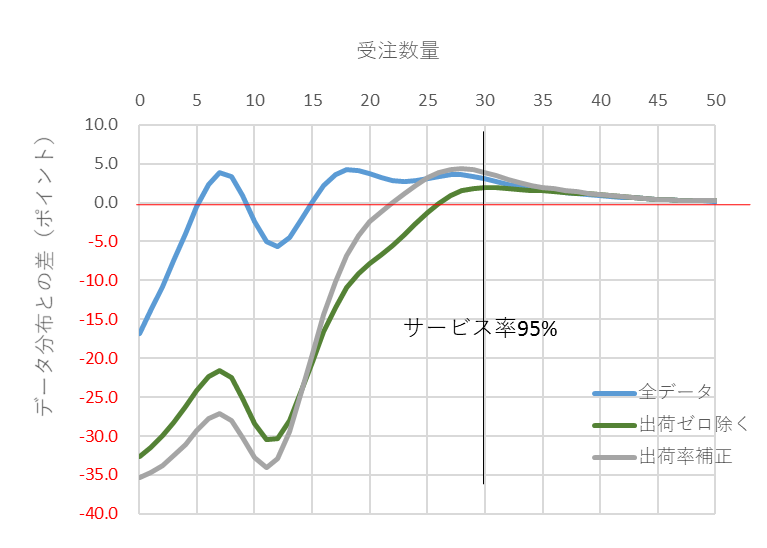
図7 間欠需要分布と①全データ、②出荷ゼロ除く、③出荷率補正のサービス率の差
図8と図9は受注件数平均が0.2のときの一例です。出荷ゼロの確率が約80%で、間欠需要の特徴が顕著に表れる領域です。図9でサービス率95%の位置で差が小さい順は①全データ、③出荷率補正、②出荷ゼロ除くですが、②出荷ゼロ除くと③出荷補正のカーブが急激に低下(マイナスの差が大きくなる)し、不安定にもなります。
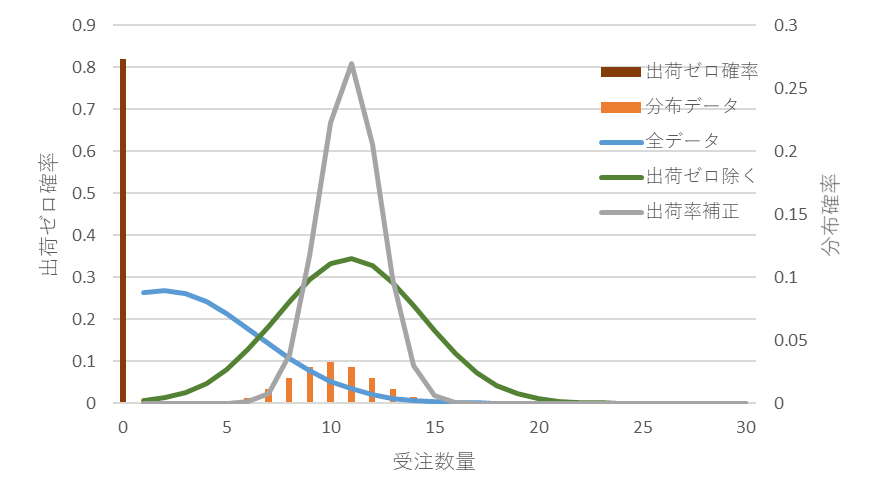
図8 受注件数平均が0.2のときの分布
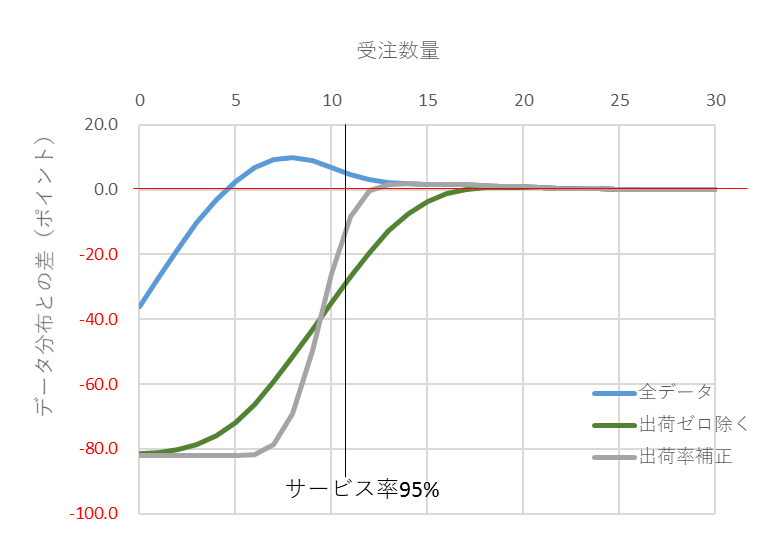
図9 受注件数平均が0.2のときのサービス率の差
図10と図11は受注件数平均が3のときです。出荷ゼロの出現確率は5%程度ですので、間欠性は弱くなり、3通りの計算の差が少なくなります。
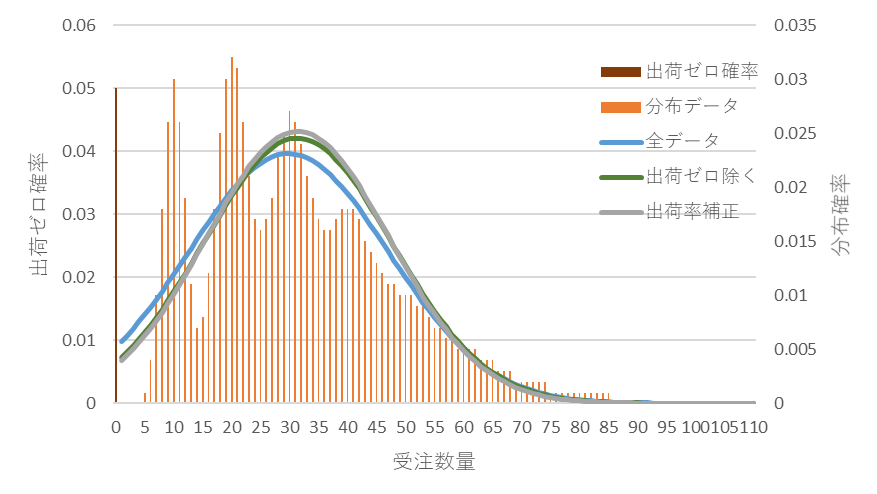
図10 受注件数平均が3のときの分布
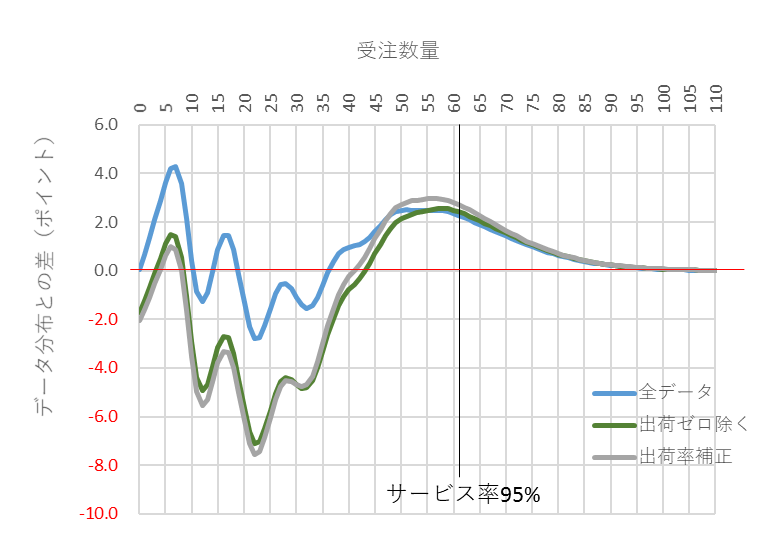
図11 受注件数平均が3のときのサービス率の差
3通りの計算方法で間欠需要の分布を計算してみました。その結果、次のことがいえるのではないでしょうか。
*間欠性が強まるほど、出荷ゼロのデータを省き、出荷率で補正する方法は機能しない。
*間欠需要のデータをそのままを使い(出荷ゼロのデータを数量ゼロとして計算に入れる)、平均、標準偏差を求める方がよさそうである。
出荷ゼロのデータは、出荷がない、という情報であって、そのデータをないものとすることは、データを改ざんしているとも考えられます。また、出荷率での補正も、なぜ、標準偏差を小さくするように補正するのか、根拠が不明です。データをそのまま使って、平均と標準偏差を計算すればよい、ということになります。当たり前のことですね。
とは言え、間欠需要では、その受注数量分布が非対称となり、正規分布とはズレが生じることは事実ですので、それを補正する方法は必要だろうと思います。別の補正方法を提案したいと思います。補正した結果の例を図12~図17に示します。図6~図11のそれぞれに補正を加えた場合のカーブ(赤)を追加したものです。差が小さくなると同時にその範囲も広がっていることが確認できます。
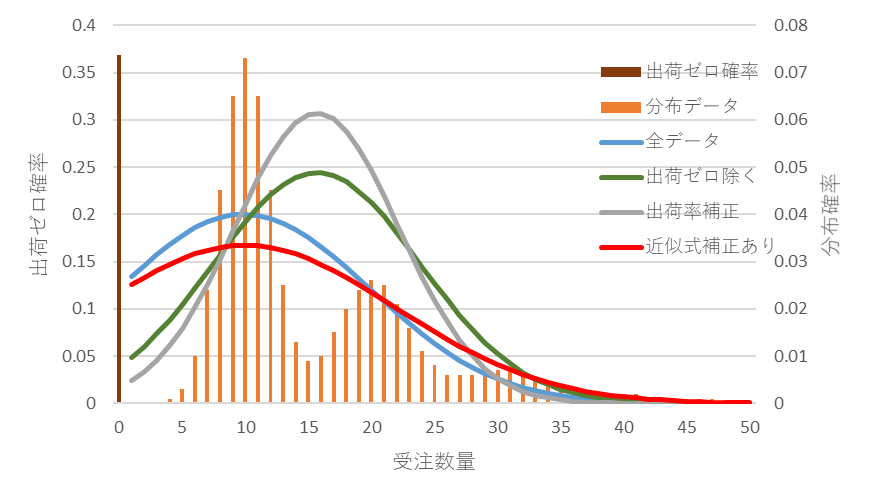
図12 受注件数平均1、補正有の分布(赤)
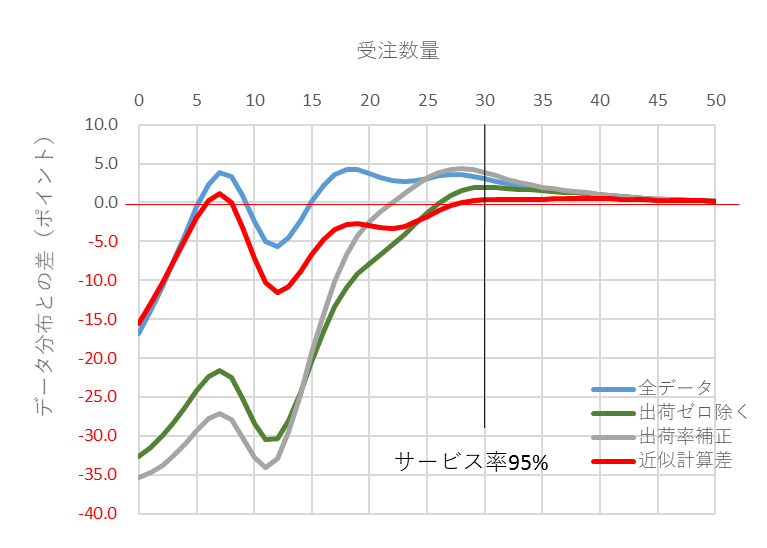
図13 受注件数平均1、補正分布有の差(赤)
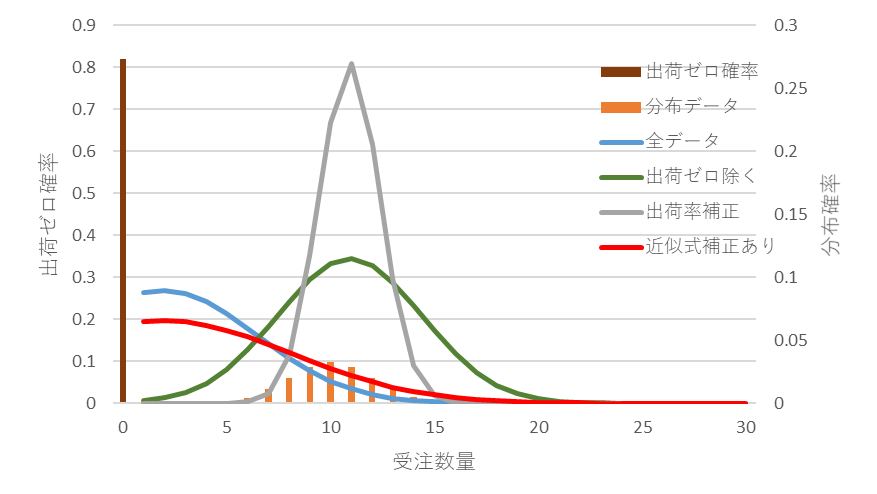
図14 受注件数平均0.2、補正有の分布(赤)
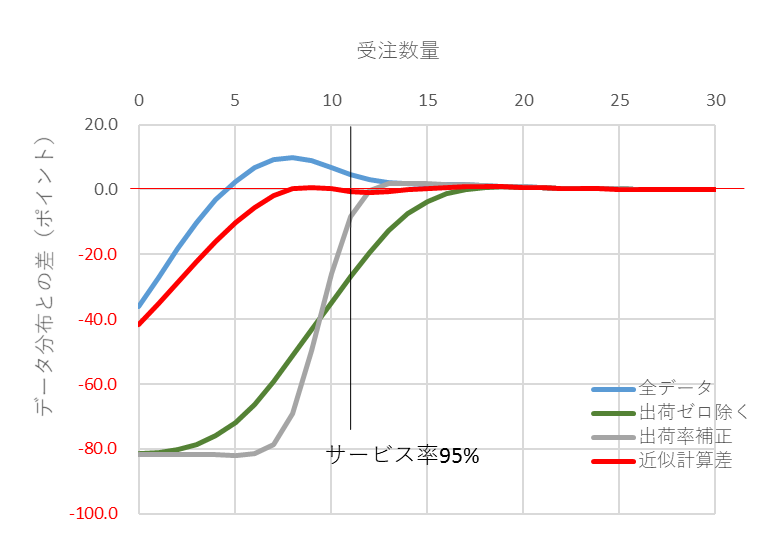
図15 受注件数平均0.2、補正分布有の差(赤)
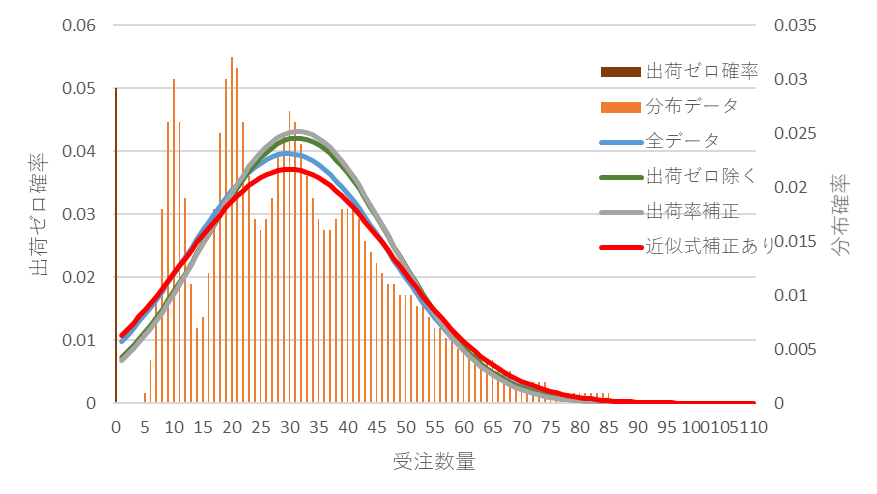
図16 受注件数平均3、補正有の分布(赤)
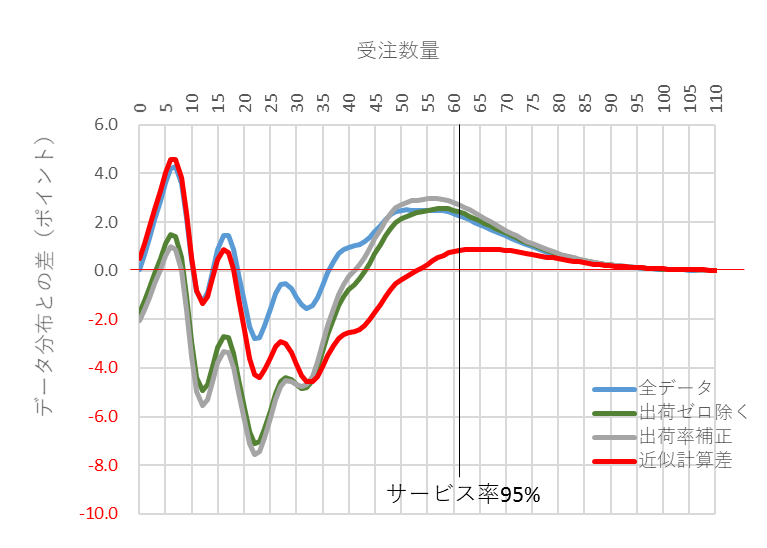
図17 受注件数平均3、補正分布有の差(赤)
どんな補正をしたかは、次回にでも、、、