No.65 受注量分散式をExcelで確認する

受注件数Nの平均 と分散Vn、１件当り受注数(以下、量/件)の平均と分散Vqがわかっているとき、受注量の平均と分散Vdは次の式で求めることができます。

  -------(式１)

-----(式2)

この式、平均はいいとして、分散については“疑わしく”思う方が多いようなんです。世の中どこを探してもないようで、そのようなものが簡単に、「はい、これです」と言われてもにわかには信じがたいんでしょうね。「そんなに簡単でいいの」という反応を示す方もおります。数学の得意な方、おりましたら、証明していただければ助かります。

数学的な証明ではありませんが、エクセルを使った計算例で、上式の実用性を確かめてみたいと思います。図1をご覧ください。

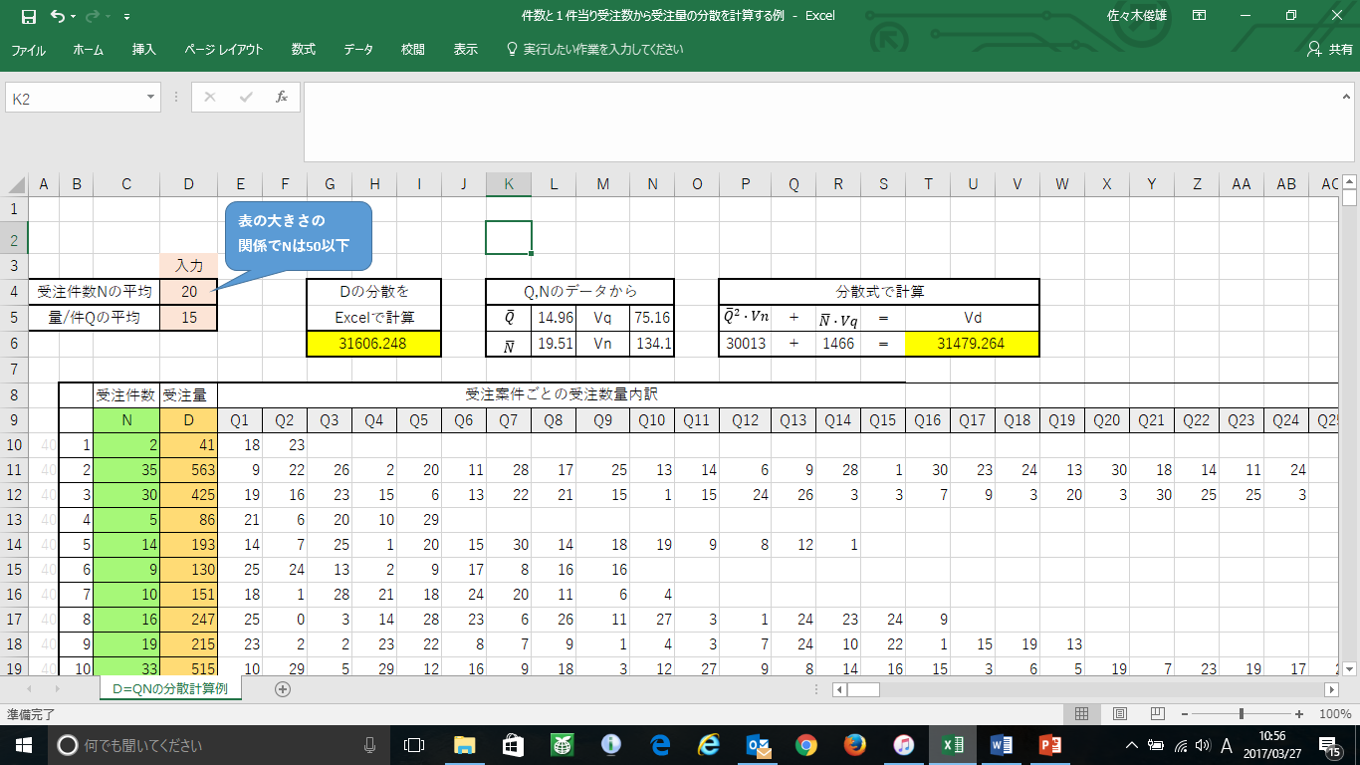
図1　エクセル・スクリーン画面

入力する数値は「受注件数Nの平均」と「量/件Qの平均」です。ピンク色の部分です。Nの平均は表の大きさの制限がありますので、50以下にしてください。Qの平均は制限ありませんが、あまり大きいと「####」となりますので、ほどほどに。Nの平均値に乱数をかけて受注件数を算出しています。緑の欄です。Q1、Q2、、、はQの平均に乱数をかけて算出しますが、Qの個数と受注件数は一致します。受注量DはQ1+Q2+・・・と数値のある部分を合算して求めています。

「Dの分散をExcelで計算」は、Excelの分散を求める関数を使ってVAR.P(D10:D1009)で求めた値です。、Vq、、Vnはそれぞれの表の値をExcelで求めた値です。

「分散式で計算」は　、Vq、、Vnの値を使って、と およびを計算したものです。

このExcelファイルをご希望の方は、「DNQ分散式Excelファイル希望」と記して、お問合せ からご連絡ください。

「Dの分散をExcelで計算」した値と「分散式で計算」した値（どちらも黄色のセル）を比較します。整数に丸めていますので、ドンピシャリとはいきませんが、実用的には充分な程度で合っているのではないかと思います。Excelファイルを入手された方は、いろいろな数値を入れて、遊んでみてください。

ところで、（式２）を導き出す過程で２確率変数XYの分散式を使いました（No.64参照）。で、実生活の中で、２つの確率変数が対称な例というものがあるかどうか、探してみました。が、なかなか見つかりません。ありそうで、ない。横ｘ縦＝面積っていうのありますが、縦、横独立で、いや相関関係があってもいいんですが、確率変数として扱えるのか、、どうも違うようです。

一方、時発生データと属性データ。実生活の中ではこちらの方が特殊で稀なのではないかと思っていましたが、ところがところが、結構、あるんですね。そのうちのいくつかを表1に例示しておきました。もしかすると、この分散式（式2）、結構使えるんじゃないかなぁー、と思ったりして。

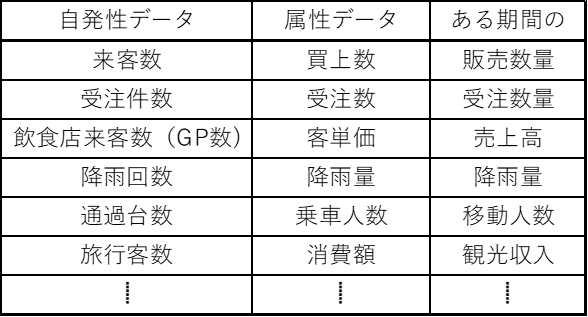
表1　自発性データ、属性データの例

（式１）（式2）の応用範囲の広さはさておき、実は、この式、これまでの在庫管理理論を一新するほどのインパクトがあることがわかってきました。次回、その辺について、愚見を、、、