No.64 受注量分散式;導出過程の1例
受注件数(来客数)の平均と分散、1件当り注文数(買上数)の平均と分散がわかっているとき、受注量(売上数)の平均と分散はどのようにして算出するか。そっちこっち、結構長い時間をかけて探してみましたが、見つかりませんでした。んで、自分で考えることにした、というわけです。
この課題を解くのに利用した平均や分散の公式みたいなのがありますので、確認しておきます。記号を使って、数学っぽくなって、難しそうにみえますが、高校程度のものです。お付き合いのほどを、、。
確率変数Xの期待値をE(X)と表します。確率変数とは、1日目の来客数は5人、2日目は7人、、というように変わる数字で、期待値とは平たく言えば平均値と考えていいでしょう。もうひとつの確率変数をYとして、XとYの積の平均E(XY)にはつぎの関係が成り立ちます。但し、XとYは互いに独立とします。
E(XY)=E(X)E(Y) -----(式1)
![]() の期待値を
の期待値を![]() 、確率変数Xの分散をV(X)としますと次の関係があります。
、確率変数Xの分散をV(X)としますと次の関係があります。
![]() -----(式2)
-----(式2)
和の分散は分散の和、という関係もあります。
V(X+Y) = V(X)+V(Y) -----(式3)
では、2つの確率変数X、Yの積の分散V(XY)はどうなるか。チャレンジ!
(式2)のXをXYに置き換えて、
![]()
(式1)を使って、
![]() -----(式4)
-----(式4)
(式2)から次の式が導き出されます。
![]() および
および ![]()
これらを(式4)に代入して、
![]()
となります。式を展開して、
![]()
後ろの2項はなくなり、整形して、
![]() ----(式5)
----(式5)
となります。
(式5)が2つの確率変数の積の分散ということになります。
平均はなんとかなりそうなので後回しにして、分散に集中したいと思います。で、(式5)を応用して受注件数Nと1件当りの受注数Qで求められる受注量Dの分散、つまりV(D)=V(QN)を求められないか、なぁー、と思ったわけです。
(式5)の構造をよくみてみますと、2確率変数X、Yの積の分散は、Xの分散成分、Yの分散成分とXYの分散成分で成り立っているということがわかります。X、Yが対称だということにも留意しておきましょう。まとめると表1のようになります。
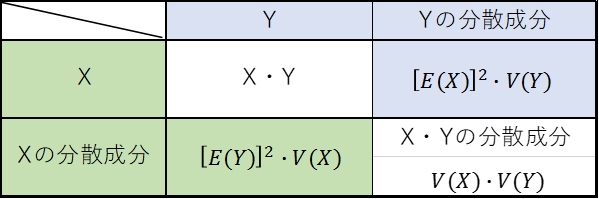
表1 2つの確率変数の積の分散
XをNに、YをQに置き換えればいいんじゃないの? と簡単に考えてしまったのですが、そう簡単ではありません。壁にドンとぶつかってしまいました。QとNとDの関係を調べてみると、表2のような構造をしているんです。先に申し上げましたが、Qは属性データですが、Nは時発生データです。QとNは対称ではないんですね。ですから、XYの分散式は、そのまま使うわけにはいかないんです。でも、全く使えないわけでもなさそう、、。
で、何とか使えないかと、もがくわけです。とりあえず、XをNに、YをQに置き換えてみましょう。分散成分という視点でみてみますと、QN の分散は、Nの分散成分、Qの分散成分、QNの分散成分の3つから成るはずだ、と考えられます。但し、QとNは対称ではないので、その条件を考慮する必要がある、と。これで、いいかどうかはわかりませんが、とりあえず、やってみましょう。
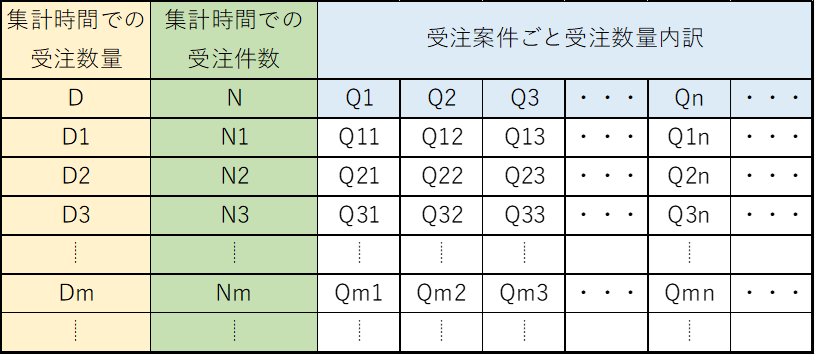
表2 受注量、受注件数、量/件の構造
では、Nの分散成分からみてゆきましょう。
DはNの属性であるQを乗じて得られます。これはXにYを乗じたのと等価なので、Dの分散V(D)のNの分散成分は次式で表すことができると考えられます。
![]() -----(式6)
-----(式6)
次に、Qの分散成分ですが、こちらは、ちょっと、違うんですね。Dは、積算ではなくて、次式のように、QをN回加算して得られるとみることができます。
D=Q1+Q2+・・・+Qn -----(式7)
このときDの分散V(D)は、
V(D)=V(Q1+Q2+・・・+Qn)
となります。(式3)V(X+Y) = V(X)+V(Y)を使って、
V(D)=V(Q1)+V(Q2)+・・・+V(Qn)
となります。V(Q1)=V(Q2)=・・・=V(Qn)=V(Q) ですから、
V(Q1)+V(Q2)+・・・V(Qn)=V(Q)N
Dのデータ数がmだとすると、Qの分散成分は次のようになります。
V(Q)(N1+N2+・・・+Nm)/m=V(Q)E(N) -----(式8)
次にQNの分散成分はどうなるか、QとNの分散成分の違いをみてみます。
(Qの分散成分) D=Q1+Q2+・・・+Qn N個のQを加算する
(Nの分散成分) D=QN Nの属性であるQを乗じる
算術計算では両者の値は同じですが、QとNの分散成分間に相互対称な乗算関係がありませんので、QNの分散成分は生じないと考えられます。
まとめると、V(D)は次のようになります。
![]() -----(式9)
-----(式9)
表3にDの分散成分をまとめてみました。
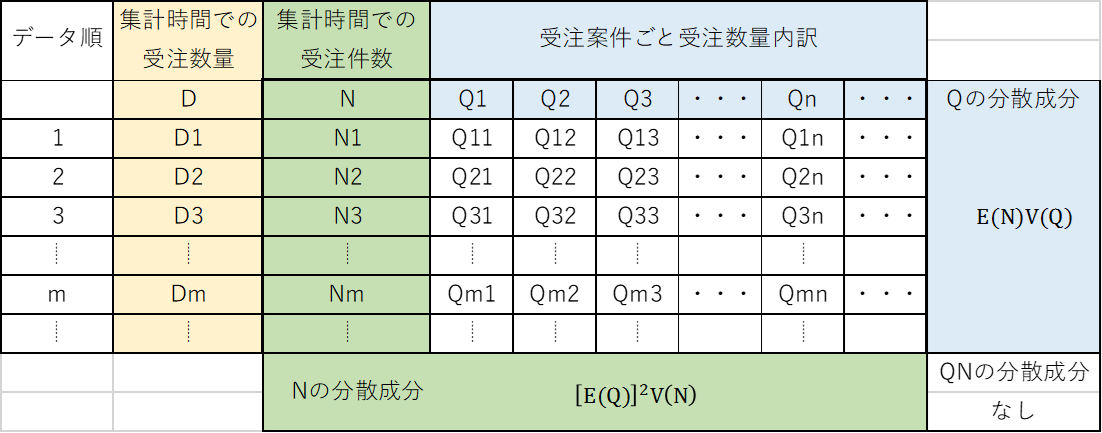
表3 Dの分散成分のまとめ
E(Q)→![]() 、 E(N)→
、 E(N)→![]() 、 V(N)→Vn、 V(Q)→Vq と表現を変更して、V(D)=Vdは次のようになります。
、 V(N)→Vn、 V(Q)→Vq と表現を変更して、V(D)=Vdは次のようになります。
![]() ----(式10)
----(式10)
平均は次のようになります。
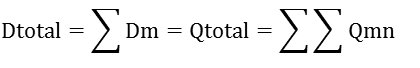
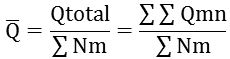
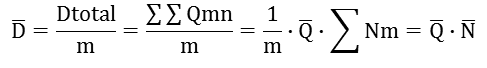 ------(式11)
------(式11)
また、安全係数をαとして、Dの最大Dmaxは、次の式で表すことができます。
![]() ----(式12)
----(式12)
(式10)、(式11)、(式12)が受注量を算出する基本的な式となります。