No.63 需要の構造をきちんと捉えよ！

生産管理でも在庫管理でもそうなんですが、需要というものがすごく重要です。どちらも需要あってのことですから、、ね。最近つくづく思うんですが、需要の捉え方がきちんとしていないんじゃないかと。生産管理、在庫管理の本をめくっても、Webでみるコンサルタントや専門家のコメント、説明をみても、そんな感じを強くするんです。危機感さえ感じてしまいます。ということで、今回は、需要の構造について考えてみたいと思います。

先ず、需要はここでは数量で捉えることにします。金額で捉えますと経済的な意味合いも含んで歪んじゃいますので。需要の構成要素は、具体的いえば、小売店では来客数と１人当りの買上点数、B to Bでは受注件数と１件当りの注文数、ですかね。小売店では小売りという通り１人当りの買上点数が比較的小さいと思いますが、B to Bでは１回で大量の取引が行われることが多いと思います。

１件当りの注文数が少ない場合と多い場合で、在庫管理上の違いはあるのでしょうか。一度にドーンと注文が来たら、在庫はあるの？　って気になりますね。直観的に欠品しやすくなる、と思われる方が多いんじゃないかと思います。いやいや、１件当りの注文数が少なくても、注文件数が多くなったら、やっぱり、欠品するよ。うん、同感。

実は、現在の在庫管理では受注件数と１件当り受注数を分けて受注量を捉えていないんです。多頻度配送がいいとよく言われます。多頻度になれば一度に納入する数量は少なくなります。手間暇を考えたら１度にまとめて納入した方が効率はいいんですがねぇ。でも多頻度がいい、と。つまり、受注件数（発注側では発注件数）と１件当りの受注数（発注側は発注数）は、分けて捉える必要があることを示唆しているんじゃないでしょうか。でも、現行の在庫管理では、この２つをまったく識別していないんです。ですから、多頻度配送がいい、という理論的な説明はどこにもない。ことばでつづられたストーリーはありますが、、。

需要の構造はいたって簡単で、受注件数と１件当り受注数。

受注件数は１日何件とか、1カ月で何件とか、ある時間間隔で集計します。もちろん集計期間ごとにバラツキます。１件当り受注数も10個であったり50個であったり、バラツキます。需要も当然ばらつきますので分布で捉えることになりますが、その分布は多くの場合正規分布に近似し、平均値と標準偏差という統計量で把握します。

受注件数を数える集計時間は、決めておく必要があります。まとめると、ある期間の受注数量を決める要素は、
①集計時間
②集計時間の間の受注件数
③１件当り受注数
の３つである、ということがわかります。

この３つの要素は、どのような関係で受注数量（需要量）を構成しているのか、これが需要の構造ということになります。構造を明らかにするためには、それぞれの要素の統計的特徴を理解する必要があります。

先ず、１件当り受注数の統計データとしての性質について考えてみましょう。小売店の一人当たりの買上点数では、比較的少数である程度のバラツキが予想されますが、B to Bでは客先が定量発注しているのか定期発注しているのかによって、だいぶ、違いがありそうです。定期発注なら１件当り受注数は変動しますが、定量発注なら一定。しかし、複数の会社から注文をもらっているとすれば、A社の定量発注数は50個、B社は80個などと、顧客ごとに異なるのではないかと思います。これは、成人の身長や体重、テストの得点、卵１個の重さ、、等と同類で、個々の性質を表していますので、属性データと呼んでおきます。

一方、受注件数は、ある時間の間に来る注文件数です。常連客からの注文も一回きりの注文も、１個の注文も100個の注文も、１件の注文は1件。小売店で言えば、背の高い客も太った客も関係なく１人は1人。1度に5個買う客も、1個しか買わない客も1人は1人。昨日来た客が今日も来たら、それも一人。1日間で平均10人来るとすれば、1週間（7日間）では70人ぐらいじゃないか、という計算も成り立ちそうですね。受注件数、来客数は時間の経過で発生するので、時発生データと呼んでおきます。図1参照。

図1　受注数量、販売数量の構成要素

受注件数という時発生データと１件当り受注数という属性データは、統計的性質がかなり違うんですね。その性質を詳しく調べて、需要の構造を明らかにしていきますが、その前に、大まかな構造をイメージしておきたいと思います。図2をご覧ください。需要は時発性データが基本で、それに１件当り受注数の属性データが掛け合わされてくる、といった構造が想定されます。

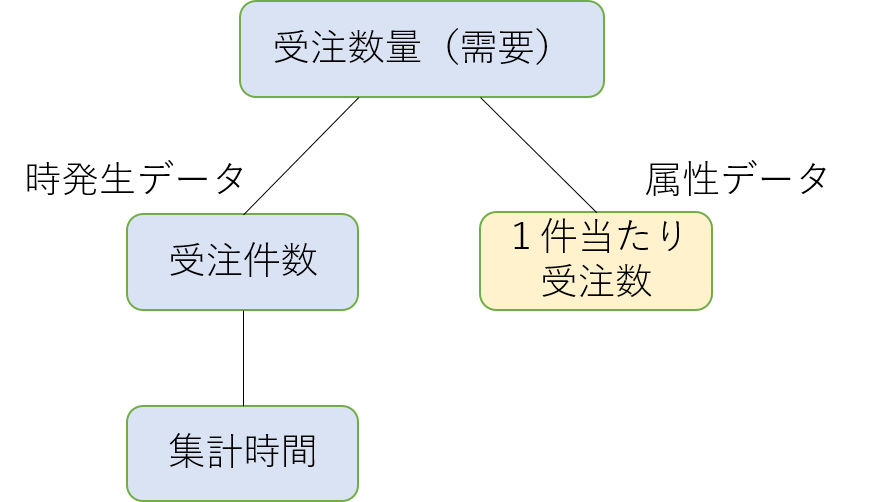
図2 需要の大まかな構造

時発生データである受注件数が主流であるようにみえますので、受注件数からみていきましょう。ひとつの注文を受け取ったとき、１件の受注と数えます。次に注文を受け取るのはいつか、ということですが、B to Bで顧客が定期発注していれば、いつ注文が来るかわかります。定量発注していればだいたいの予測はできますが、バラツクでしょう。顧客数が複数なればばらつき具合は大きくなります。小売店では、10分後に来るときもあれば3時間後にやっと来た、などバラバラで、ランダムですね。総じて言えば、ある程度の規則性はあるがランダムである、と言えるんじゃないかと思います。規則性を利用することはできますが、問題はランダム性。ランダムをどうとらえるか、なんて悩まないで、ここは先人の知恵を拝借することにします。ランダム到着にはポアッソン分布がピッタシ、なんだそうで、、。

ポアッソン分布の例を図3に示します。来客平均が１人～５人のときの分布を示しています。表1は平均来客数が2人のときの0人、1人、、、６人が来る確率を示してます。人数の分布ですから、整数しかとらない離散型分布となります。また、平均来客数が５人以上では、その分布は正規分布に近似してきます。ポアッソン分布は平均と分散が等しくなりますので平均来客が５人のポアッソン分布の分散は5。同じ平均、分散の正規分布を重ねたものを図4に示します。

ポアッソン分布でもうひとつ重要な性質があります。ポアッソン分布の平均は単位時間に来客する平均ですから、来客数の平均は時間に比例することになります。また、平均と分散が等しいので、来客数の分散も時間に比例することになります。

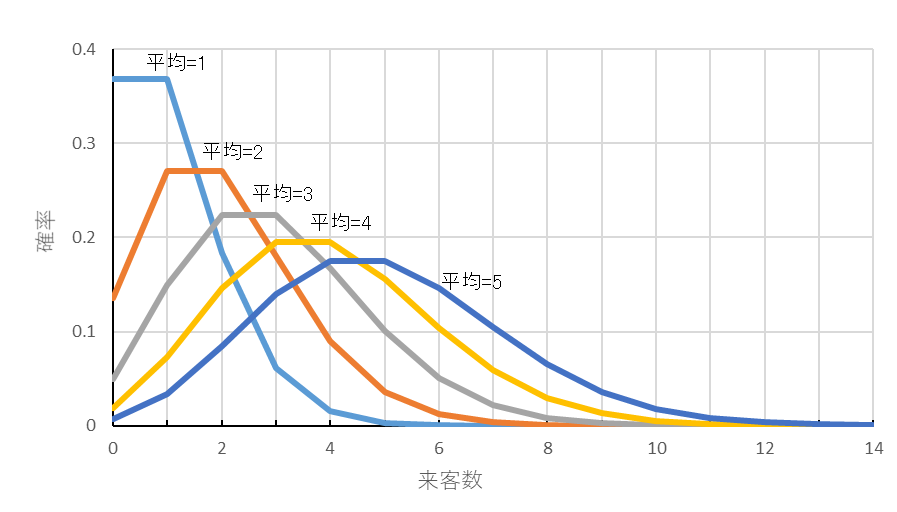
図3 ポアッソン分布の例

表1 平均来客数2人のときの来客数が0人～6人の来る確率

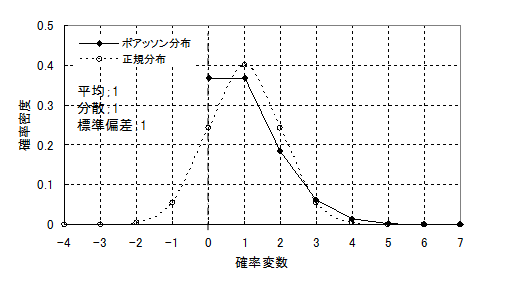
図4 平均5のポアッソン分布を正規分布で近似するときの差

平均4以下のポアソン分は正規分布で近似することは難しいのだはないかと思われます。特に平均が1とか2の場合は正規分布とは似ていません。これについては後で考えることにします。

来客数の分布を捉えることができました。次に、一人当たりの買上点数（以下、数/人）の分布について考えてみます。数/人は属性データですので、多くの場合、正規分布に近似すると考えられます。データから平均と標準偏差を求め、分布を把握することができます。

ここまでをまとめますと、
＊来客数はポアッソン分布し、平均と分散は等しく、両者とも時間に比例する。また、平均5以上は正規分布に近似する。
＊数/人 はおおむね正規分布する。

次に、来客数と数/人 のデータから販売数を算出してみます。来客数は時発生データ、数/人は属性データと性質が異なります。販売数は、この性質の異なる来客数と数/人で決まりますが、どのような数式で求めればいいのでしょうか。販売数の平均と分散を求めてみます。

販売数の平均＝(来客数の平均) X (数/人の平均)

平均は簡単ですね。問題は、分散。どうやって求めればいいのか。考えてみましたが、よくわからないので、そっちこっち探し回りました。思しき専門家の方々にも聞いてみました。が、結局、わからず。需要予測や在庫管理、生産管理でも、販売数を来客数と数/人に分けて捉えることは行われていないようなんです。そんな必要性もなかったんでしょうか。

しかし、前述しましたように、B to Bでは受注件数と１件当り受注数の識別は、在庫管理上重要である、、、のではないか、と。多頻度配送をよしとする定性的な説明だけでは効率の良い在庫管理の仕組みを構築することはできません。在庫管理の説明がどこか胡散臭いと感じる原因のひとつは、こんなところにもあるのかもしれません。

で、分散。これを求める式って、どこにあるの？