No.59 安全在庫の計算式は誤り!?
在庫管理の課題を語るとき、安全在庫という切り口も面白いと思います。バラツキ、変動がなければ在庫管理はすごく簡単です。欠品の主要な原因がバラツキや変動だからです。そのために安全在庫なるものが必要なわけですが、その量を決めるのはそんなに簡単ではないようです。安全在庫のまわりには、在庫管理の悩みや苦労が集積しているのではないか、、そんな思いから、安全在庫にまつわる話をしようかな、と思って、、。
先ずは、安全在庫の定義から。下記は、最も一般的な安全在庫を求める式です。
![]()
在庫管理に携わっている方ならお馴染みの式だと思います。定期発注では√の中が(発注サイクル+リードタイム)となりますが、話は上記の式で進めていきたいと思います。
ところが、ところが、大事件。この安全在庫の式は間違っているというのです。ある在庫管理のコンサルティング会社のWebsiteにこんな説明があるのです。
~~~~~~~~~~~~~~
下記の安全在庫計算式は、科学的な誤りであることが判明した。
![]()
なぜならば、ディメンジョンチェックをこの計算式に適用すると
![]()
となって、左右両辺の単位が一致しないからである。
~~~~~~~~~~~~~~
しろうとのたわごととは違います。特許取得済みの独自在庫管理を売りにする、コンサルティング会社のWebsiteですよ。
安全在庫の計算式から話を始めようかと思っていましたので、それが誤りだとなれば、話を始めることもできなくなりました。いきなり、出鼻をくじかれたというか、、。困りましたねぇ。
何はともあれ、「安全在庫計算式誤り説」の真贋を確認。インターネットを探し回りましたが、出所は一カ所。まだ世の中に広まっている様子はありません。「安全在庫計算式誤り説」に賛同の意見も異論も見つかりません。
自分で考えてみることにしますか。範囲を安全在庫に関連するところ、つまり、バラツキに関連する領域を中心に考えてみたいと思います。
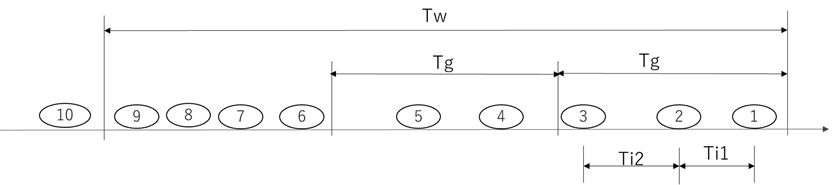
図1 注文の到着
始めに、需要がどのように捉えられるかを考えてみます。図1は注文が来る様子を示しています。注文①が来てから②が来るまでの時間を受注間隔Tiとします。受注間隔はランダムにバラツクのが普通です。立て続けに来ることもあればパラパラとしか来ないときもある。つまり需要は時間経過の中で、ランダムに発生すると考えられます。
だとしたら、需要の大きさは受注間隔で捉えればいいことになります。例えば、平均受注間隔が50分で、そのバラツキ(標準偏差)は10分とか。受注間隔が短くなればなるほど受注量は多くなります。しかし、普通、需要は数量で捉えますし、在庫は数量で管理しますので、受注間隔で捉えるのは違和感があります。やっぱり、数量で捉えないと、、。
ランダムに来る注文を数量に変換するためには、ある一定の時間(集計時間;Tg)を決め、その間に来る注文数を数える方法が考えられます。Tgは1日であったり、1週間だったり、1カ月だったりといろいろです。
Ti間隔で到着する注文はTg間では、(Tg/Ti)件の注文が来ることになります。これはTg間の受注件数を示すわけですが、時間/時間ですので、無次元になります。待ち行列理論では「平均到着率」と言っています。「率」ですから単位はありません。値が1以下の場合は%や歩合を使いますが、受注件数は1以上ですから、適していません。単位はありませんが、適用する環境で「来客数(人)」とか、「インターネットのアクセス数(件)」とか、都合の良い単位名を新たに付けたりします。在庫管理では「受注件数」となります。
数量に変換するためには、受注1件の受注数量をかけます。ここでは話を簡単にするため常に1個/件 とします。
Tg間に来る注文数量Dgは次のようになります。1は1個/件を意味します。
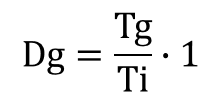
Dgは、図1の例では、3個、2個、4個、、、ときて、そのデータを集計してDgの分散Vdgと標準偏差Sdgを計算します。これで需要量を数量で捉えることができます。
安全在庫計算式にはもうひとつ、時間があります。納入リードタイムです。それをTwとします。Twでの注文数量をDw、その分散をVdw、標準偏差をSdwとします。
安全在庫は納入リードタイムでの標準偏差に安全係数をかけたものですので、次のようになります。

いま、Tg=1日、Tw=3日で、Vdg、Sdgと安全係数がわかっているとします。納入リードタイムTwでの安全在庫を計算するためにはSdwを既知のデータで置き換えればいいわけです。
受注間隔の母集団は変わらないものとします。図1でわかりますように、ランダムに到着する注文をTgという時間間隔でサンプリングしていると考えれば分かりやすいと思います。
Twでの受注数量Dwの分散Vdwは、データを集計しなおせば計算できます。そのようにして求めてもいいわけですが、もっと簡単な方法があります。それは分散の加法性という性質を利用する方法です。Tg=1日での受注数量の分散Vdgを用いて、Tw=3日での受注量の分散Vdwを次のように計算することができます。
Vdw=Vdg+Vdg+Vdg=3・Vdg
Tw=3日での受注量の標準偏差Sdwは次のようになります。
![]()
ここで重要なことは、3という数字の背後にあるディメンジョンを正しく理解することです。需要のもともとは受注間隔という時間が単位です。それを集計時間という別の時間枠で到着注文件数を数えて、(数量/件)をかけて数量に変換しているわけです。Tgを集計時間、Twを納入リードタイムと呼びましたが、長さの違いだけで、どちらも同じ時間です。つまり、3は、次の式で計算されているわけです。
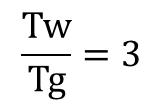
(Tg/Ti)は数学的には無次元ですが、「単位時間での受注件数」という単位がぴったりです。(Tw/Tg)も無次元ですが、わかりやすい単位名称が見つかりません。くどくどと書けば、「需要量の標準偏差を算出した時の集計時間に対する納入リードタイムの倍率」ということになりますが、、。
Tg=1日、Tw=3日のとき、(Tw/Tg)も納入リードタイムも数値は3と同じになりますが、例えば、集計時間Tg=5日、納入リードタイムTw=20日だったら、
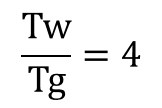
納入リードタイムは20日ですが、Tw/Tgは4。数値も違ってきます。この式でディメンジョンチェックをしてみます。

右辺の[時間]/[時間]は無次元になりますので、左右の単位は一致することになります。
ですから、安全在庫の式を下記のように表現すればわかりやすいかもしれません。

(√内の分子と分母の時間単位は同じにする必要があります)
次に、世の中ではどんな説明がされているのか、一例を紹介します。「経営数学入門―待ち行列理論と在庫管理」藤本佳久著ではこんな風に書いてあります。(調達期間を納入リードタイムに置き換えてあります)
~~~~~~~~~~~~~~
単位期間当たりの需要量の標準偏差をσ、納入リードタイムをL単位期間とすると、
![]()
~~~~~~~~~~~~~~
説明文を言い換えると、需要量の標準偏差σを算出した期間を単位期間として、納入リードタイムはL単位期間とする、となります。
Tg=1日、Tw=3日の場合、σ算出の単位期間は1日、1日を単位期間として納入リードタイムは3単位期間となります。3日ではなく、3単位期間です。
Tg=5日、Tw=20日の場合は、σ算出の単位期間は5日、5日を単位期間として納入リードタイムは4単位期間となります。20日ではなく、4単位期間です。では、Tg=7日、Tw=25日なら、σ算出の単位期間は7日、7日を単位期間として納入リードタイムは、≅3.57単位期間となります。小数でも問題はありません。
ここでの単位期間というのは、時間の単位を持っているわけではありません。「需要量の標準偏差を算出した時の集計時間」を1単位としましょう、ということです。単位期間というと時間を連想しますが、名前はなんでもいいわけです。それを単位として、納入リードタイムは何倍であるか、つまり、比率ですので、無次元になります。
二通りの方法で安全在庫計算式のアルゴリズムをみてみました。多少の違いはありますが、結論は同じ。つまり、√の中は[時間]の単位ではなく、無次元の数値になりますので、式の左右のディメンジョンは一致する、ということになります。
「安全在庫計算式誤り説」の根拠とした式左右のディメンジョンの不一致。これは、√内の値に時間のディメンジョンがあるという誤認が原因でした。「安全在庫計算式誤り説」は誤りである、という結論になります。
巷の情報はどうなっているか、ザットみてみると、70%ぐらいは、標準偏差を算出した集計時間と納入リードタイムの関係に言及しています。但し、説明の不正確さや曖昧さがあり、√の中の「リードタイム」「発注リードタイム」「納入リードタイム」「調達期間」等は、時間単位を持っているかのような印象を与えてしまっているように感じられます。
実際は、集計時間は1日、1週間、1月間ということが多く、納入リードタイムの単位に気を付けていれば、間違いは起こりにくいと思われます。特に疑問を持たずに使ってきたのではないでしょうか。しかし、「ディメンジョンが合わないから、安全在庫計算式は誤りだ」というメッセージに、みなさまはどのように感じられたでしょうか。
「そう言われれば、そうなのかぁ」
半信半疑で、消極的ではあっても、かなり多くの人がそう思ったのではないでしょうか。それが問題なのです。しかも、思いのほか、深刻かもしれないんです。
一方どこかで、疑義を感じ、反論を試みようと思った方もいるのではないでしょうか。次回、さらに話を進めてまいります。
ご意見、ご質問、お叱り等ございましたら、[お問合せ] からお寄せください。