No.55　間欠需要、出荷ゼロ日を省いて計算？

注文がある日もあれば、ない日もあるといった需要を間欠需要と呼ばれています。間欠需要の需要の平均と分散を計算するとき、巷の在庫関連の書によれば、

「出荷がゼロであった日のデータはカウントしない」

と書いてあります。複数の書に同じように書いてありますので、在庫管理の世界では標準的な計算方法なんでしょうね。

前々から、ちょっと変だな、と思っていました。出荷がゼロなら、出荷数量をゼロとして計算するのが普通で、そのデータを省くというのは、どういうことだろうか、と。「出荷なしの日のデータはカウントしない」と記述してある書籍の著者、二人に質問してみましたが、まともな返答はありません。

しょうがないから、自分で考えてみることにします。

具体的な例で考えてみます。受注数量＝出荷数量とします。注文はランダムに来ます。指数分布に従うとします。注文がない日もあれば、1日に2件ある日もあり、平均すると1日1件の注文があります。1件の注文の数量は平均20個、標準偏差５個でバラツクとします。シミュレータで計算した一例を図１に示します。30日のうち11日は注文がありません。間欠需要ですね。

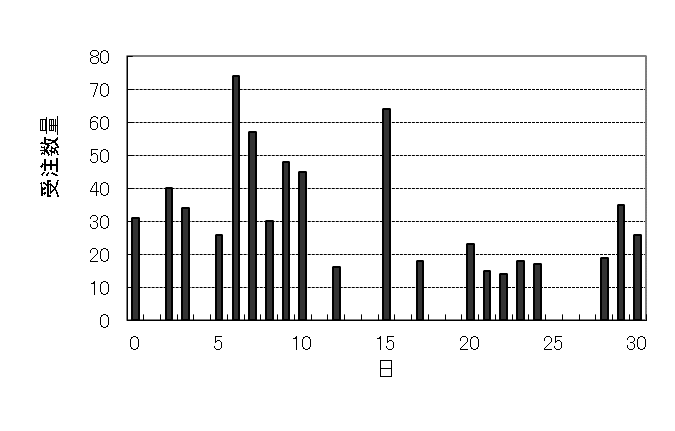
図１　日ごとの受注数量の推移

図２は受注数量の分布です。受注数量ゼロの棒が目盛範囲を超えて高くなっています。分布は右側にすそ野を引いています。

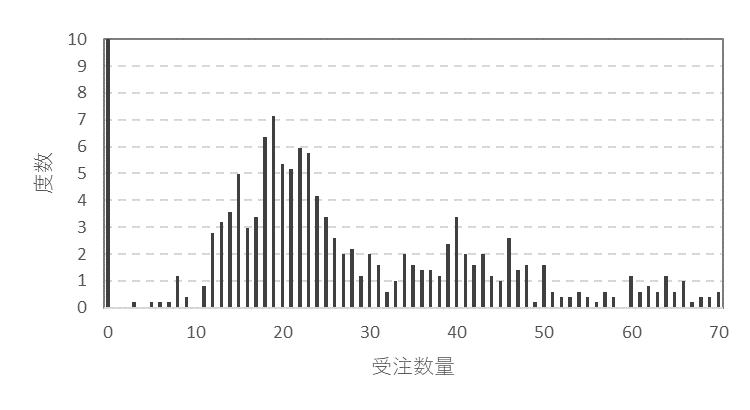
図２　日ごと受注数量の分布

同じデータを、今度は、1週間（7日間）ごとに受注数量をとってみると、図３のようになります。注文のない週はありません。間欠需要ではなくなりました。

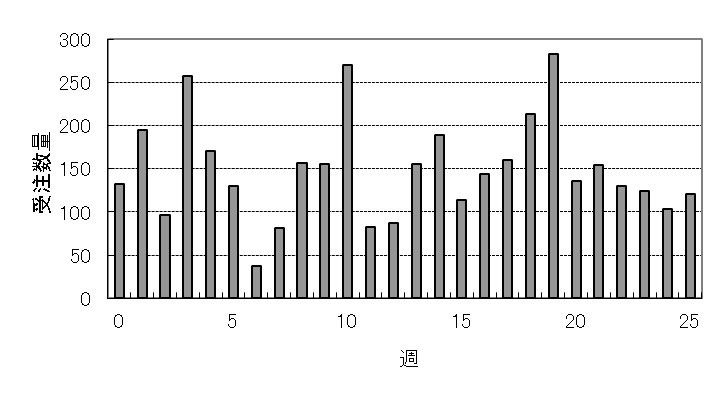
図３　1週間ごとの受注数量の推移

図４は受注数量の分布です。受注数量ゼロの週はありません。

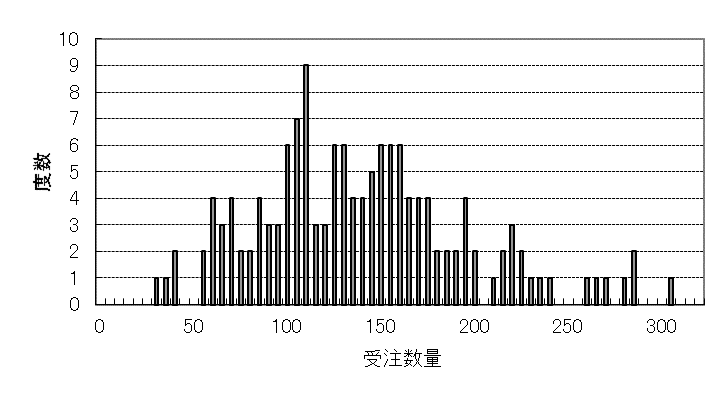
図４　週ごと受注数量の分布

まったく同じデータですが、それを週単位でまとめれば注文のない週はありませんが、日単位でまとめると注文のない日が出てくる。では、月単位でまとめれば、、、当たり前ですが、注文のない月はありませんね。

間欠需要になるかどうかは、注文の到着間隔と受注観測期間との関係で決まるんじゃないでしょうか。注文の到着間隔＞受注観測期間　のとき、間欠需要状態になる。間欠需要が特別な状態ではなく、受注の集計の仕方、見方によって間欠需要にみえたり、そうでなかったりする、ということですね。

言い換えますと、同一の母集団から、観測期間（この例では、日とか週）を振ってデータ（この場合受注数量）をとったら、どのような分布になるか、という課題になります。先ず、理論的なアプローチを試みてみます。

需要分布の設定を次のようにします。
　＊受注到着間隔；平均1日の指数分布
　＊1件の受注数量平均（量/件）；20個、標準偏差５個の正規分布

1日間の平均受注件数を、その分散を、　量/件の平均を、その分散をとして、

受注数量平均、およびその分散は次の式で求められます。

（詳細な説明については「STIC発注方式」を参照ください）

数値を入れてみます。

観測期間を1週間としますと、平均値、分散とも7倍になりますので

シミュレーションで出てきたデータ（データ数1,000）を、出荷のない日の出荷数をゼロとした場合と出荷のない日を除外した場合の二通りで計算してみました。理論計算の結果とともに表１にまとめてみました。

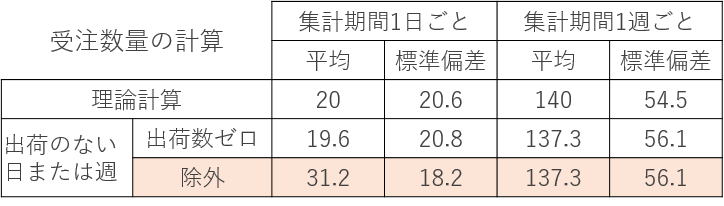
表１　シミュレーション・データから受注数量の平均と標準偏差を計算

観測期間が１週ごとのとき出荷のない週はありませんので、「除外」も「出荷数ゼロ」も同じ値になります。出荷のない日の出荷数をゼロとして計算した結果は理論計算値とほぼ同じですが、それを除外して計算した場合は平均値が高くなり、標準偏差は小さくなってしまいます。

間欠需要の平均と分散、標準偏差を計算する際の留意点をまとめますと、
＊間欠需要とは、注文の到着間隔＞受注観測期間　のときに、受注観測期間（日とか週とか、）の注文がゼロとなることで起きる。
＊どのような需要の母集団でも、受注観測期間を短くしていくと、間欠需要状態になる。
＊注文ゼロのデータは統計理論上、意味を有する。そのデータを省くことは、データの改ざんとなり、データ処理を歪めることになる。

反論、叱責等、おおいに歓迎します。お問合せからお願します。