No.42 かんばん方式の対変動特性
かんばん方式と発注点方式をシミュレーションで比べてみました。かんばん方式の方が明らかに勝っていることが分かりました。かんばん方式の特徴をさらに詳細に分析してみたいと思います。
受注数量の平均と分散は次の式で表せます。
![]() (式1)
(式1)
![]() (式2)
(式2)
ここで、
受注間隔の平均; ![]() 、その変動係数;Ci
、その変動係数;Ci
補充時間の平均; ![]() 、その変動係数;Cr
、その変動係数;Cr
補充時間での受注件数の平均;![]()
数量/件の平均; ![]() 、その変動係数;Cq
、その変動係数;Cq
補充時間での受注数量の平均; ![]() 、その分散Vdr
、その分散Vdr
在庫管理の基本的メカニズムは、受注をトリガーにして、在庫補充時間での最大受注数量に相当する流動インベントリーが回転する、と捉えることができます。(式1)と(式2)で流動インベントリーの大きさを算出します。
かんばん方式に適用するときには、次のような読み替えをすると分かりやすいと思います。
受注間隔;後工程の部品の消費時間間隔
補充時間;かんばんがはずされてから引き取りが完了するまでのリードタイム
数量/件;かんばん1枚の部品点数(パレット収容数量)
基本的な動きをみるために、数量/件を1としましょう。その変動係数Cqはゼロとなりますので(式2)は次のようになります。
![]() (式3)
(式3)
かんばん方式も使い方によって定量不定期発注になったり定期不定量発注になったりします。ある一定枚数のかんばんがはずれたらそれを一括して戻す場合は定量不定期、ある一定時間ごとに、かんばんを戻す場合は定期不定量。前に発注点方式とかんばん方式を比べましたので、かんばん方式は定量発注だ、という印象が付きまといますが、必ずしもそうではありません。
定量とか定期とかではなくて、かんばんが1枚はずれたら直ちに戻せば、かんばんの滞留時間が短くなって、かんばん枚数もその分少なくなります。ただ、全体のかんばん枚数が多いときは、かんばんを戻す作業が増えてしまいます。そういう時はかんばん1枚の部品点数を増やすのも一策です。但し、待ち時間が出てくるでしょう。
かんばんを戻す方法でみると、定期不定量と定量不定期、そして、かんばんが1枚はずれたら直ちに戻すという即時の3つがある、ということですね。かんばん1枚の部品点数が複数のときは、即時の場合も定量不定期となってしまいますが、、。
かんばん1枚の部品点数の制限をなくしたらどうなるか。一般的な環境では、1件の注文数量はいろいろ。3個だったり、10個だったり。受注して出荷した分だけ直ちに発注することにすれば、発注時刻も発注数量もバラバラ。つまり即時発注=不定期不定量発注ということになります。
ちょっと脱線しましたが、一般の在庫補充では、即時発注=不定期不定量発注が基本で、発注頻度が多くなりすぎるときは定量や定期発注にする、というのが在庫管理の基本ではないか、ということです。これは重要なことですので、後で詳しく述べることにします。
話を戻します。流動インベントリーを求める式から、かんばん方式の特徴をみてみます。ここでは、何枚かのかんばんを溜めて、一度に運ぶ場合について考えてみます。定量不定期発注ですね。遅れ時間が生じますので、この時間遅れが受注数量の平均と分散にどのような影響を及ぼすか、を考えてみます。
一括して移動するかんばん枚数をKaとします。かんばんがKa枚まで溜まる平均時間を ![]() とすれば、
とすれば、
![]()
となります。この時間だけ補充時間Trは長くなります。調達リードタイム(発注から納入までの時間;かんばんが戻されてから部品とともに帰ってくる時間)をTpとすれば、
![]()
となります。従って、受注数量の平均 ![]() は、Q=1としていますので、次のようになります。
は、Q=1としていますので、次のようになります。
![]() (式4)
(式4)
ここで、調達リードタイム間の件数; ![]()
受注数量の分散はどうなるでしょうか。注目するポイントはかんばんがKa枚溜まるまでの時間のバラツキです。この変動係数をCtkaとしますと、次のような関係があります。
![]()
この変動分が加わります。ここでの補充時間Trは調達リードタイムTpとなりますので、Vdrは次のようになります。
![]() (式5)
(式5)
ここで、調達リードタイムの変動係数;Cp
まとめますと、
* かんばんをKa枚一括して運ぶ場合、必要なかんばん枚数はKaだけ増える。(当たり前ですけど、、)―――(式4)参照
* かんばん枚数の分散は、 ![]() だけ増える。(こっちがポイント)―――(式5)参照
だけ増える。(こっちがポイント)―――(式5)参照
ということになります。
(式4)と(式5)で ![]() 、
、 ![]() として、CiとCpを0~1で振って、Ka=5とKa=10で必要かんばん枚数を計算してみました。その結果を図1に示します。
として、CiとCpを0~1で振って、Ka=5とKa=10で必要かんばん枚数を計算してみました。その結果を図1に示します。
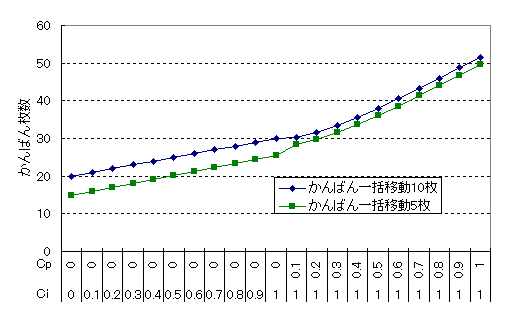
図1 必要かんばん枚数の計算例
計算した結果とシミュレーション結果の相関をみてみましょう。図2はかんばん枚数の計算値とシミュレーション結果の相関です。安全係数は3として、 ![]() で計算してあります。良く一致していることが分かります。
で計算してあります。良く一致していることが分かります。
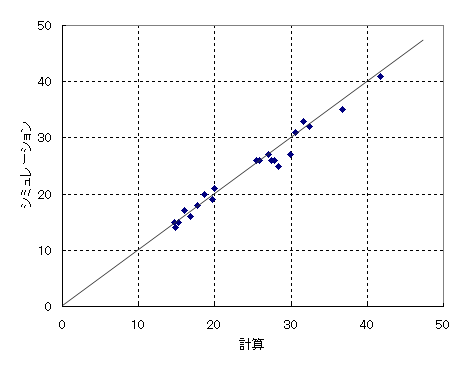
図2 かんばん枚数の計算結果とシミュレーション結果の相関
計算結果やシミュレーション結果から、確かに、バラツキが少なければ、必要かんばん枚数も少なくて済みます。バラツキが大きくなればかんばん枚数も多くなります。かんばん枚数を求める式があれば、その程度が分かり、かんばん方式が使えるかどうかの判断もしやすくなるんじゃないかと思います。
「平準化なくして、かんばん成立せず」の呪文があってか、かんばん方式をランダムな変動条件で使ってみる、などという考えはご法度だったんでしょうね。もう、そんな呪縛から解放されてもいいんじゃないかと思います。
かんばん方式は、もしかすると、在庫補充の理想的メカニズムではないのか、という期待、いや、単なる妄想かな、も感じます。そんなこともあたまの片隅に置いて、次回は、一般的な在庫発注方式へと展開し、在庫補充のメカニズムの理解を深めていきたいと思います。