No.40　発注点方式とかんばん方式を比べてみました

かんばん方式では、かんばん枚数の振れが3%以内でないとダメだ。だから平準化が絶対条件だ、と巷の本に書いてあります。ほんとうに、そうですかぁ？ということで、変動要因を加えたら、かんばん方式はどうなるか、調べてみたわけです。詳細はNo.39をご覧ください。分かった事は、変動があってもかんばん方式って、使えるんじゃないの、ということでした。

かんばん方式が一般の在庫管理に利用できるとなれば、いろいろとメリットがありそうですね。ということで、発注点方式とかんばん方式を比べて、具体的に同様な利点があるかをみてみたいと思います。

簡単な例を設定します。注文が来る時間間隔を10で一定、調達リードタイムを100で一定とします。時間の単位は、分でも時間でも日でもかまいません。但し、通して同じ単位を使うこととします。時間を一定にしたのは、初めに基本的なメカニズムを知りたいからです。

発注点は、調達リードタイム間の需要量ですので、10個となります。変動はありませんので安全在庫はゼロ。在庫と注残の推移を図1に示します。縦軸は在庫数、横軸は単位在庫の動きの順番ですが、この場合は、時間に換算できます。初めに15個の在庫があります。横軸5のとき在庫が10個となり、同時に10個発注したことを示しています。横軸15のとき、入庫して在庫となります。と同時に10個発注します。以降、これを、繰返します。

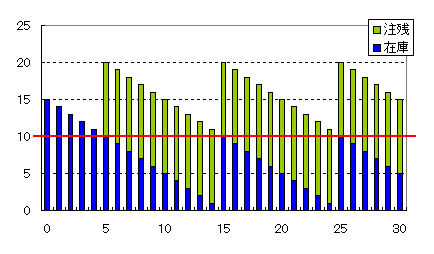
図１　発注点10（赤線）、発注量10

図2は発注量を15個にしたときの在庫と注残の推移です。在庫と注残の合計値のピークは２５個となります。

図2　発注点10、発注量15

次に、発注点を15個にして、発注量を10個にしてみました。結果を図3に示します。在庫と注残の合計値のピークは25個と同じですが、最低の在庫量に違いがみられます。

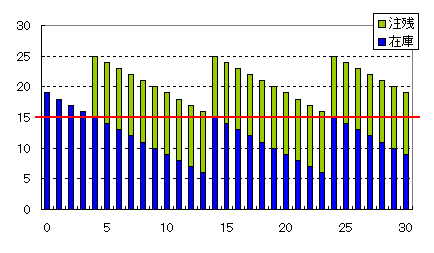
図3　発注点15、発注量10

では、発注点が8個、発注量は10個ではどうなるでしょうか。結果を図4に示します。需要量はそのままで、発注点を下げましたので、欠品が発生します。欠品数は発注回数が増すごとに増えていきます。

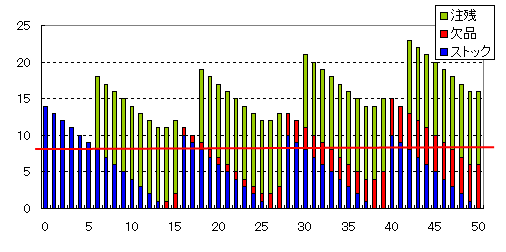
図4　発注点8、発注量10

発注点を10個で発注量を8個にした場合は図5に示すような結果になります。ある時点より在庫がなくなりますので、欠品状態が継続することになります。

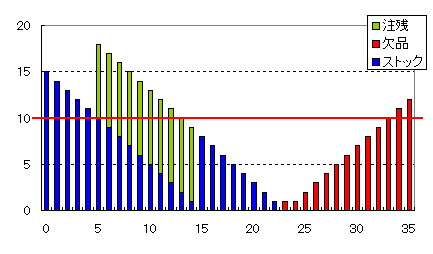
図5　発注点10、発注量8

発注点方式の基本的なメカニズムを概観してみました。まとめますと、

* 調達リードタイム間の需要量（以下設定発注点と記す）よりも実発注点が低いときは、発注ごとに欠品数が増える。
* 設定発注点よりも発注量が少ないときは、ある時点より欠品状態となる。
* 設定発注点より発注量が多いときは在庫＋注残の合計値のピーク値が上り、発注回数が減少する。
* 設定発注点より実発注点が高いときは、安全在庫が増える。
* 設定発注点＝実発注点＝発注量が、回転在庫が最小となる限界条件である。

では、同じ需要に対して、かんばん方式を適用して見ましょう。かんばん枚数は調達リードタイム間の需要量をパレット収納数で割ったものですが、ここではパレット収納数は1個とします。一品一葉で、かんばん枚数＝単位在庫数とします。発注点方式と比べるため、かんばんの移動を10枚単位で行うことにします。そのときの補充時間は調達リードタイムにかんばんが10枚溜まるまでの時間（100）を加えた時間ですので、200となります。在庫（20個）すべてにかんばんがついている状態を初期状態とします。結果の1例を図6に示します。

時間軸10でかんばんが10枚となりますので、一括して移動します。時間軸20で在庫とともにかんばんが戻ります。以降、繰返します。

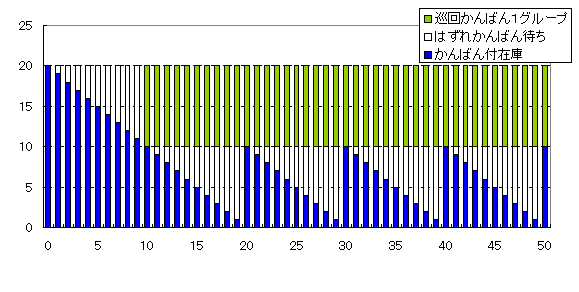
図7　かんばん方式；かんばん15枚一括移動

かんばん移動を5枚一括にします。図8に示すように、かんばんは15枚で回ります。

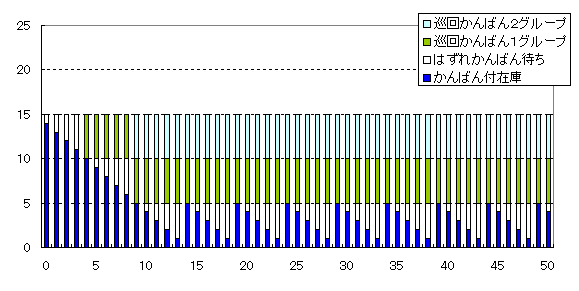
図8　かんばん方式；かんばん5枚一括移動

かんばんがはずれたら直ちに移動すると、図9に示すように、かんばんは10枚で回ります。

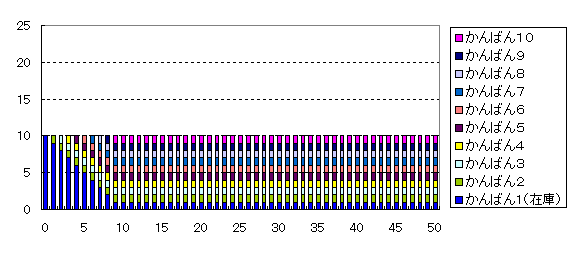
図9　かんばん方式；かんばん1枚ごとに移動

発注点方式とかんばん方式を比べてみました。欠品を起こさない在庫量で比べてみましょう。在庫量は、発注点方式は在庫＋注残、かんばん方式はかんばん枚数としますと、発注点方式では最低在庫量は20個、かんばん方式では10個とかんばん方式の方が少なくなります。発注点方式は発注点以下の発注量にはできませんが、かんばん方式ではそのような制限はありません。但し、発注量を少なくすると、発注回数は増えます。

このような比較では、かんばん方式の方が優位ですが、需要変動、調達リードタイムの変動があった場合は、どうなるんでしょうね。次回検討してみます。