No.39　「平準化なくして、かんばん成立せず」に惑わされるな！

補充時間Trの間の受注数量の平均 とその分散Vdtrは次の式で表すことができます。

                  (式1)

        （式2）

ここで、 は数量/件の平均、Vqは数量/件の分散、 は受注件数の平均、Vn(ti)は受注間隔Tiの変動に起因する受注件数の分散、CtrはTrの変動係数です。

この式を使って、かんばん方式を分析してみたいと思います。かんばん方式については、業界、学会等で、様々な研究がされているようです。関連する論文も数え切れないほどあって、もう研究し尽くされているっていう感じですね。

かんばん方式（図1参照）は、原理は簡単なんですが、失敗例も多数報告されています。うまくいかない原因のひとつが平準化できてないこと。かんばんの振れが3%以内じゃないとダメ、とか言われています。3％の根拠ってどんなことかと、調べてみたんですが、納得するような説明はみつかりませんでした。多分、論文の中にはあるんだろうと思いますが、、、

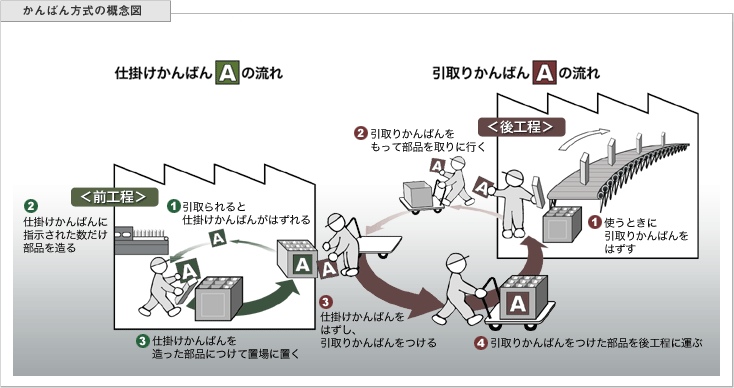
図１　かんばん方式の概念図（出展；トヨタ自動車株式会社Website）

かんばんは、「仕掛けかんばん」と「引き取りかんばん」があります。「引き取りかんばん」は運搬、「仕掛けかんばん」は生産ラインを経由して回りますが、原理はどちらも同じ。但し、「仕掛けかんばん」は生産ラインの特性が影響しますので、かんばん枚数が多くなるんじゃないかと思います。

引き取りかんばんをイメージしてみましょう。かんばん枚数の計算式はつぎのようになっています。

かんばん枚数=(D x Lw + Is)/u 少数以下は整数に切り上げ

ここで
D；平均需要量
Lw；かんばんがはずされてから引き取りが完了するまでのリードタイム
Is；安全在庫数量
U；パレット収容数量

具体的に数字を入れて確認してみましょうか。1日の稼働時間は8時間とします。
D=48/日
Lw=2時間（0.25日）
U=4個

ここまではいいんですが、Isはどのようにして求めるんでしょうか？　とりあえずゼロとしましょう。そうすると

かんばん枚数＝48x0.25/4=3

で、かんばん枚数は3枚。U=3のときはかんばん枚数は4枚となります。まったく変動がない場合はこれでいいのですが、現実はそうはいきません。

で、かんばん方式の安全在庫について考えてみたいと思います。使うのが冒頭に挙げた（式1）と（式2）です。かんばん枚数の式の(D x Lw + Is)で、D x Lwの部分はLw間の消費数量で（式１）、Isの部分は消費数量のバラツキで、（式2）で表すことができると考えられます。その式を使ってみます。
ここで、
Lwの平均を 、その変動係数をClw、
Lw間の消費数量の平均を 、その分散をVdlw、
部品の消費間隔（消費頻度）をTcns、その変動係数をCcns

とします。 とVdlwは（式1）と（式2）を変形して、次のようになります。

         （式3）

       （式4）
（ここではQが1となり、Vqは0ですので、（式2）の第二項はなくなります）

Dlwの最大値は安全係数を標準偏差の3倍として、次の式で表すことができます。

かんばん枚数は次のようになります。

    を整数値に切り上げ

安全在庫を求めるためには、変動要因を確認する必要があります。（式4）でわかる通り、消費間隔の変動（Ccns）とLwの変動（Clw）の二つです。u=3およびu=4の場合、Clw=0のままで、Ccnsだけを0～1に振ってみました。そのときの必要なかんばん枚数がどうなるかを計算した結果を図2に示します。

後工程での部品を消費する時間間隔のバラツキ（Ccns）が大きくなると、必要なかんばん枚数は増えていくことになります。Ccnsが1では0のときと比べて、かんばん枚数は2倍になります。

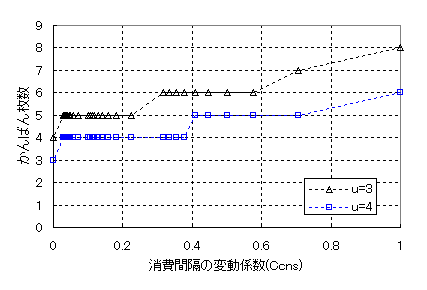
図2　消費間隔の変動とかんばん枚数の関係

今度は、Ccns=0のままで、Clwだけを0～1に振って、必要なかんばん枚数がどうなるかを計算してみます。結果は図3のようになりました。こちらの方は、Clwに対して指数関数的にかんばん枚数が増えていきます。Clwが1だと、0のときと比べて、かんばん枚数は13倍になります。

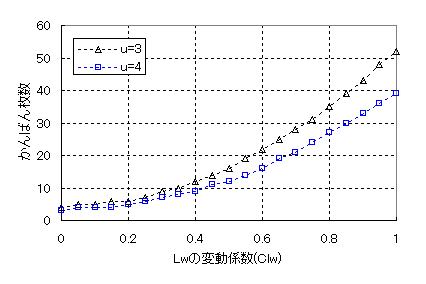
図3　Lwの変動とかんばん枚数の関係

CcnsとClwは独立と考えられますので、両者が重なれば、かんばん枚数も加算されることになります。

この二つのグラフはかんばん方式の基本的な特性を表しているのではないかと思います。平準化がかんばん方式成立の絶対条件となっているのはなぜか。推定される理由は、

* バラツキが大きくなると、かんばん枚数が急に多くなり、仕掛が増え、その結果リードタイムが長くなり、品種の切替に時間がかかるなどして、生産性が低下する。
* バラツキが大きくなると、必要なかんばん枚数が急に増え、その結果かんばんが足りなくなり、回らなくなる。生産ラインは混乱し、工場の生産性を著しく低下させる。

このようなことに結びつくのは、かんばん枚数が指数関数的に増加するLwのバラツキの影響が大きいのではないかと考えられます。少しのバラツキでかんばん枚数が急激に増える。かんばん枚数を増やさない（仕掛を増やさない）ためには、バラツキを極力少なくしなければならない。そのためには平準化生産ができていなければならない。了解。

少し、視点を変えてみましょう。バラツキをありのままに受入れると、かんばん方式はどうなるか。例えば、後工程の消費間隔のバラツキの変動係数が1となると、かんばん枚数は2倍になります。であれば、かんばん枚数を2倍にしておけば、後工程のバラツキを吸収できるのではないか。後工程が不特定多数でも良し。複数の顧客からランダムに舞い込む注文でも、不特定多数の客が来る小売店でも、あるいは、親会社からの発注がばらついて困ると嘆く下請けでも、かんばん方式は使えるかも、、、。

但し、仕掛けかんばんの場合、補充時間（Lw）のバラツキについては管理の仕組みを構築する必要があると思います。かと言って、平準化が絶対条件ではありません。補充時間のバラツキをある範囲に抑えることで、指数関数的に増えるかんばん枚数を抑えることができます。（補充時間のバラツキを抑える方法については動的生産管理を参照下さい）

かんばん方式はトヨタ生産方式と一体化して理解されていますが、在庫管理論的視点からみれば、極めて基本的でオーソドックスな方法です。ですから、あらゆる生産環境で、かんばん方式の原理は利用できます。平準化ができないために、かんばん方式をあきらめた企業はたくさんあると思いますが、「平準化なくして、かんばん成立せず」に惑わされてはいけません。