No.34　受注件数と数量/件に分解してバラツキを捉える

受注数量の分布は平均と分散が分かれば、その平均と分散（または標準偏差）が同一である正規分布に置き換えて、最大値を推定（計算）することができるのではないか、という話をしました。

少し気になることが残っています。受注1件当りの数量に関することです。前回、何げなく触れたのですが、もう少し詳しく検討しておく必要があるのではないか、と。

受注1件当りの数量を数量/件とします。受注数量は受注件数と数量/件で決まります。一般的には、受注件数も変動し、数量/件も変動します。そのとき受注数量はどのようなバラツキになるのか。ここが気になるところです。

例えば、受注件数の平均が10件、数量/件の平均が30個のときの受注数量と、受注件数の平均が30件、数量/件の平均が10個のときの受注数量は同じなのかどうか、ということです。直感的には、どちらも平均は300個で同じであろうと思われますが、バラツキ具合はどうなんでしょうね。

在庫管理の本を数冊、みてみましたが、受注数量を受注件数と数量/件に分けて説明してある本はないんですね。でも、ですよ。あるとき、いつもの数量/件の5倍の数量の注文がきたら、欠品するなんていうこと、よくありますよ。そんなのは異常だから、気にしなくていいのかな？　いや、そういうことじゃなくて、数量/件の大きい注文が来れば、受注数量のバラツキも大きくなるんじゃないかな、という感じがするわけですよ。

気になることは、後々まで残さない方がいい。ここで、じっくり、考えておきましょう。

ここから、数式が出てきますが、それほど難しくはありませんので、お付き合いの程よろしくお願いします。

受注間隔をTi、集計時間をTg、受注件数をNとしますと、Ti、Tg、Nの間にはN=Tg/Tiの関係があります。例えばTgが8時間でTiが2時間であればNは4（件）となります。Nのデータ数をmとすると、Tg間の平均受注件数は次のようになります。

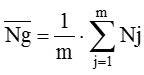
一般的には注文数量は注文ごとに異なります。数量/件をQとしますと、データ数mの受注数量の合計Qsumと、数量/件の平均は次のようになります。

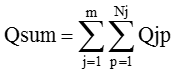
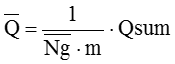
受注数量をDとして、Tg間のDの平均 は次のようになります。

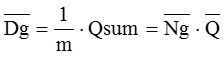        （式1）

受注数量の平均は比較的簡単な式で求めることができました。次に受注数量の分散を求める式を導き出してみたいと思います。

顧客からの注文の母集団は単一であるとしましょう。集計時間Tgは一定として、受注間隔Tiの分散を 、受注件数Ngの分散をVng、数量/件Qの分散をVq、受注量Dgの分散をVdgとします。

Vdgは、データ数がｍのとき、次の式で求めることができます。

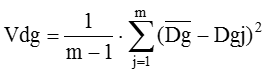
ここで、Qの分散Vqをゼロに近づけてみます。Vq=0となり、そのときQは となります。式(29-1)を代入すると、Vdgは次のようになります。

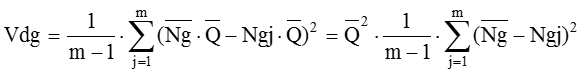
Vngは、 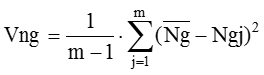ですから、

Vdgは 　　 となります。

次に、Ngの分散Vngをゼロに近づけます。Vng=0となり、そのときNgは となります。Ng個のVqのデータの合計がVdgとなりますので、Vdgは次のようになります。

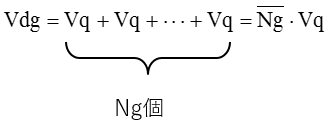
Vq=0およびVng=0の境界条件で考えてみましたが、NgとQは概ね独立と考えられますので、それらの分散は加法性に従うと考えられます。そうしますとVdgはつぎのようになります。

       （式2）

（式2)を受注量分散式と呼ぶことにします。

少々、ややこしかったですかね。数式だけでは分かりにくいし、本当にそうなるかどうかあやしいので、シミュレーションで確かめてみました。表１はシミュレーション条件を示しております。受注間隔Tiの変動係数をCi、数量/件Qの変動係数をCqとしています。

式２で計算した値とシミュレーションで得られた値の相関関係を図１に示します。良く一致していることが分かります。

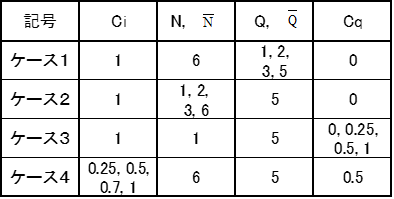
表１　シミュレーション条件

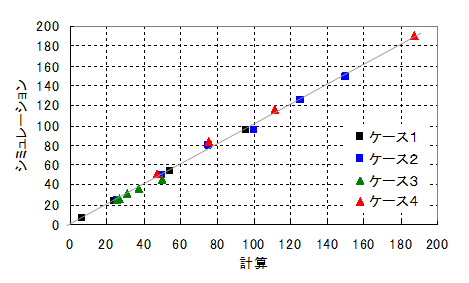
図２　計算とシミュレーションの相関図

まとめますと、集計期間Tg間の受注件数の平均を 、分散をVng、数量/件の平均を 、分散をVqとすると、受注数量の平均 および分散Vdgは次のようになります。

       （式1）

       （式2）

ちょっと、数値を入れて計算してみましょうか。受注間隔は指数分布、数量/件の正規分布で標準偏差は平均の25%とします。次の2つのケースで分布がどのようになるのかを計算してみます。

ケース１
受注件数の平均 、分散Vng=10、数量/件の平均 、標準偏差=7.5（Vq=56.25）
受注数量の平均　
受注数量の分散　
受注数量の標準偏差　

ケース2
受注件数の平均 、分散Vng=30、数量/件の平均 、標準偏差=2.5（Vq=6.25）
受注数量の平均　
受注数量の分散　
受注数量の標準偏差　

ケース１もケース２も、当然ですが、平均は同じです。標準偏差はケース1が97.8、ケース２が56.5で、ケース２の方がバラツキは小さくなります。みなさまの感覚と合っていますか？