No.33　間欠的需要や離散型分布－正規分布で代用できないか

受注間隔がどのような分布であっても、ある一定期間での受注件数は、その平均が5～6以上では正規分布に近似することを前回説明しました。しかし、それ未満では正規分布として扱うことができない。どうしたらいいのか。これが一つ目の心配事。二つ目は、一つ目と関連するのですが、受注件数が1とか2では、注文がある日もあればない日もあるという間欠的な受注パターンになる。間欠的受注パターンでは正規分布からますます離れてしまうように感じられます。どうすればいいのか。そして三つ目。受注件数の分布は、受注件数が整数ですから、離散型の分布です。連続型の正規分布で置き換えてもいいのかどうか。

この三つの心配事は、どれも関連し合っています。特徴をまとめると間欠型受注、離散型分布を滑らかな連続型分布である正規分布に置き換えて計算できるのかということだと思います。

ちょっと立ち止まって今、どこにいるか確認してみましょう。在庫管理は適正在庫とか発注点など在庫管理側が設定した基準ではなく、需要を基準にするべきだ、というコンセプトから出発しました。そのためには需要を捉える必要があります。需要を捉えるのに一番簡単そうなのがある期間での受注件数だろうと考えました。幸いにも受注件数は、受注間隔がどのような分布であっても、その平均が5～6以上では正規分布に近似することがわかりました。需要を正規分布で捉えることができれば、確率を考慮した需要の最大値を求めることができます。最大値がわかれば、準備しておく在庫数量がわかります。これが在庫管理では最も重要な項目のひとつです。

で、三つの心配事。正規分布に近似しないこと、間欠的需要パターンであること、離散型分布であることで需要の最大値の推定にどのような影響があるのか。正規分布から最もかけ離れた条件で考えてみましょう。受注件数の平均が１のポアッソン分布を例にします。これに相当する正規分布は平均が1、標準偏差が1の正規分布です。図1に両方の分布を重ねて示しています。ポアッソン分布は1、2、3、、、の整数の確率密度で、正規分布は平均1を中心に左右対称の連続分布です。

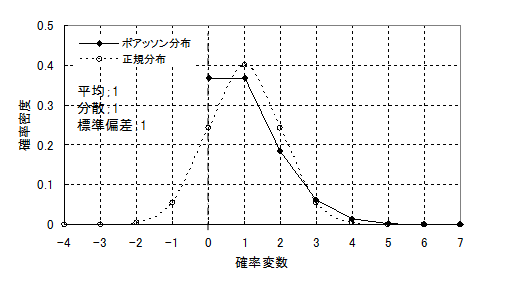
図1　ポアッソン分布と正規分布

二つの分布はどうみても似ていません。ポアッソン分布は確率変数のマイナス側はゼロで、離散型。正規分布は確率変数1を中心に左右対称の山形で、連続分布。どうしても違いが目につきます。

ここで知りたいのはなんだったか。それは需要の最大値です。最大値は分布の右側の裾野です。裾野がどうなっているかをみるのに累積確率をみるとわかりやすいと思います。図2はポアッソン分布と正規分布の累積確率のカーブです。図をみてわかるように確率変数が3（2σ）以上では両者のカーブはほぼ一致します。つまり2σ以上の領域では正規分布で最大値を計算しても実用上問題ないのではないか、と考えられるわけです。

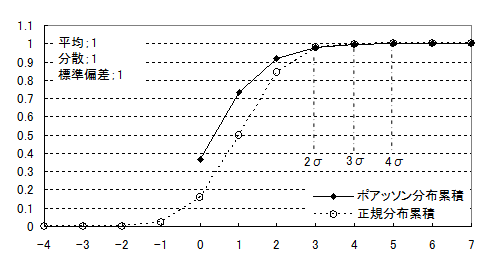
図2　累積カーブ

今度は、1件の注文で注文数が5個一定の場合を考えてみます。1件の受注で受注数量は5個、2件の受注では10個、、、となり、受注数量が2、3、4個は存在しません。平均は5、標準偏差も5となります。平均5、標準偏差5の正規分布と重ねて、受注数量の分布を図3に示します。離散型分布と連続型分布。似ていませんね。

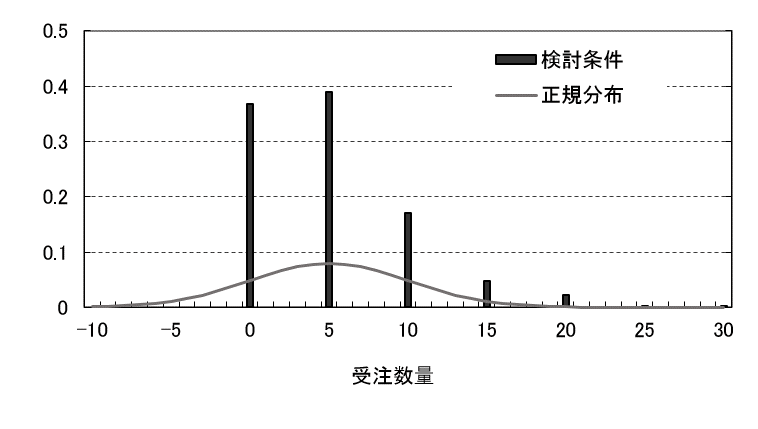
図3　受注数量の分布と正規分布

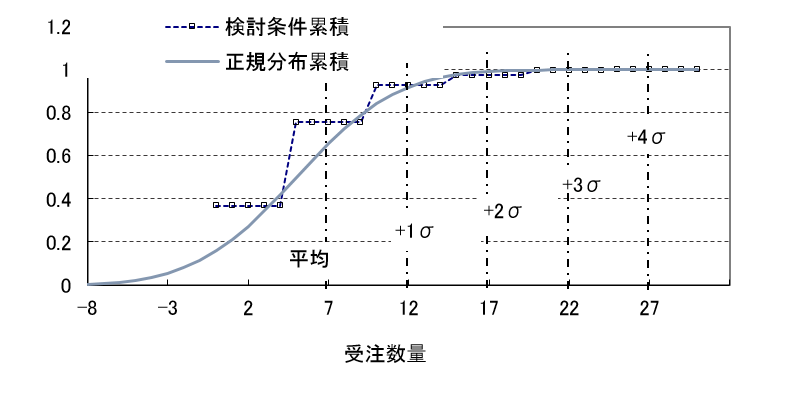
図4　累積確率のカーブ

同じように両者の累積確率のカーブをみてみましょう。図4に示します。2σ以上では正規分布の累積確率のカーブとの差は小さくなります。

次に、受注がある日もあればない日もあるという間欠型受注パターンではどうなるかをみてみます。図5にその一例を示します。

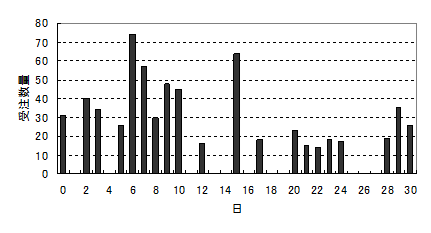
図5　間欠型受注パターン

図6に受注数量の分布を示します。注文がない日は受注数量がゼロです。その確率が高いことがわかります。正規分布の形状とはかなりかけ離れています。

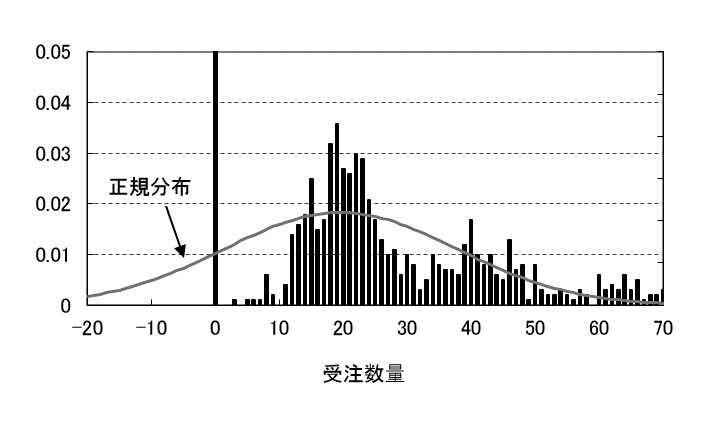
図6　受注数量の分布

図７に累積確率カーブを示しています。同じように２σ～３σ以上では正規分布との差は小さくなります。

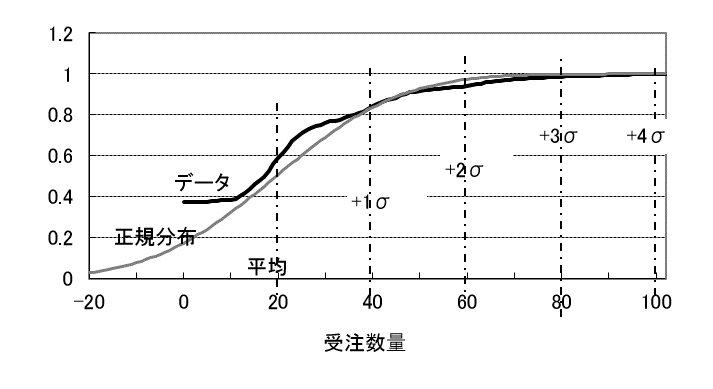
図７　累積確率カーブ

三つの心配事。正規分布に近似しないこと、間欠的需要パターンであること、離散型分布であることは、実用的にはあまり心配しなくて良さそうです。

まとめると次のようになります。
受注間隔の分布がどんな形状であろうと、ある一定期間での受注件数の平均が5～6以上では正規分布に近似する。受注件数の平均が5未満のときや間欠的な受注パターンのときは、形状は正規分布に近似できないが、平均値と標準偏差を同じくする正規分布で置き換え、最大値を計算することができる。この計算はある程度の誤差を含むが、実用上の問題はほとんどない。

すごく簡単になりました。