No.26　第1種の誤り

在庫管理は、本来はそれほど複雑ではありません。簡単なはず。でも巷に出ている本をみると、難しく書いてあるんです。読んでも良くわからないところが多いように感じています。 で前回、つらつらと、在庫管理に関する懸念、疑問などを書き流しました。疑念、疑問を呈したからには、それらに対する私の見解を述べなければならないかな、 と認識はしておるんですが、、。

在庫管理は生産管理に比べたら単純ではありますが、説明するとなると結構大変なんですよ。理由のひとつは、現在の在庫理論が定着していることじゃないかな、と感じています。現在主流の在庫管理を大雑把にいうと、定期発注では、将来の需要を見込んで発注数量を決める。定量発注では、発注点という在庫数を設定して、それ以下になったら経済的発注量で発注する、ということ、ですかね。

定期発注からみていきましょうか。在庫補充するためには一般的には、納入リードタイム＋発注サイクルタイム　の時間がかかります。となれば、その時間だけ先の将来にどれだけの需要があるか、それに合わせて補充数量を決めなければならない、と教科書には書いてあるんです。みなさんも、そういう説明で納得されているんじゃないかと思います。

で、実際は、将来のことなど誰にもわからない。これは動かしようのない事実。では、どのようにして将来の需要を予測するか。経験的に予測する。これも立派な予測方法です。経験というのは過去のデータがベースになっていますが、人によって、弱気な人、強気な人で予測値は異なります。人によらない方法としては過去のデータを集計して平均値とバラツキを求め、確率的に予測する方法もあります。

中には、予測するのが面倒だ、とばかりに、毎回平均値で発注する御仁もおります。計算することもなく、簡単で良い。長い目で見れば外れる度合いは一番少ないのではないか、という説明になんとなく納得してしまいます。

もう少し高度、というかどうかはわかりませんが、需要予測の技術を駆使して、先々の需要量をはじき出すことも行われています。精度がどの程度なのか、私にはよくわかりません。ただ、膨大な情報と高度な統計学を駆使した需要予測の精度は高いんだろうな、という印象はありますね。

需要予測なんて、当たらないって、よく言われますね。だったら予測なんかしなければいいじゃないか、となる。前述した平均値を使うというのはその具体例かもしれません。しかし、平均値というのも予測値なんです。

需要変動に合わせて発注量を決める、という考え方もあります。方法はいろいろ考えられますが、その一例は、直近の数日間の需要の移動平均値から先々の需要をはじき出し、それと倉庫在庫＋発注残を比べ、納入リードタイムを考慮して在庫が切れないかどうかを判断して、切れないと判断されるときは発注しない、切れると予測されるときは発注する。発注量は、例えば、移動平均で計算した需要量のＸ倍、というように。原理的には、受注したとき毎回、判断することになるんだと思いますが、実際は、件数が多いので、1日1回、ということになるんではないか、と思います。

この方法は、発注時期も発注数量も変動しますので、不定期不定量発注なんて言っているようです。不定期不定量というと、いいかげんな響きがありますので、適時適量発注なんていうこともあるようです。最新の需要量と倉庫在庫、そして納入リードタイムを考慮して、欠品の出ないように在庫を補充する、というこの仕組み、良さそうに聞こえますね。これが、究極の在庫補充のメカニズムだ、と書かれています。

定量発注では、多くの場合、発注点という在庫レベルを設定しています。発注点に達したら、あるいは下回ったら、予め決めておいた数量を発注する、というものです。発注点は納入リードタイム間の最大消費量（受注量）で、これは過去のデータを計算して決めます。まぁ、計算と言っても予測ですね。発注数量は、経済的発注量がいいって、本には書いてありますが、実際はあまり使われていないようです。経験的に、適当に決めてるんじゃないでしょうか。そんな精度でいい、ということですかね。

このように、在庫管理にはどこまでも予測が付いて回ります。切っても切れない、腐れ縁。予測とどう付き合うか、これが問題だ！

こういう時は、原点に帰れ。予測、バラツキ、、、の原点って？　私にとっては品質管理かなー。例えば、 管理図。ロットから4~5点、抜き取りデータを採る。平均値（ ）と移動範囲（R）を計算し、図１に示すようなチャートにプロットしていく。 Chartには中心線（黄色）と上のUCLと下のLCLの2本の線（赤色）があります。

大雑把に言えば、プロットした点が赤線内にあれば異常なし。赤線を超えれば何らかの異常あり、と判断して工程状態を管理します。（実際はもっときめ細かな項目で判断します）通常、打点は赤線以内にばらつきます。この時は異常ではないと判断し、何もしません。何もしない、ということが重要なんですよ。異常ではないので、何もしない。当たり前の話です。

では、同じ状態で、打点のアップ、ダウンに敏感に反応して、上ったら下げる操作を、下がったら上げる操作をしたらどうなるか。人為的に何らかの操作を加えるわけです。監視している特性値はその影響を受けて変化するでしょうね。上ったら下げるように、下がったら上げるように操作するわけですから、打点のバラツキは、何もしないときと比べて小さくなるんじゃないか、と期待されます。ところがそうでもない。何もしないときよりも打点のバラツキは大きくなることが多いんです。なぜでしょうね？

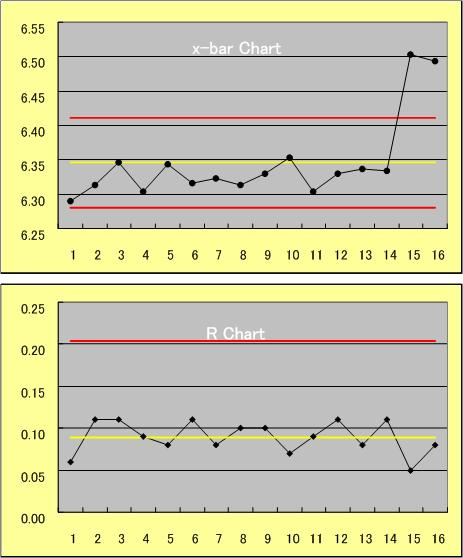
図1 管理図の一例

何もしなければ条件の変化はなし。何らかの操作を行ったために条件が変化した。ということなんですが、、

ちょっと、この表現は正しくないですね。何もしなくても条件は変化しています。ですから、何もしなくても、操作を加えても、条件は変化する、と。

では、何もしないで変化する条件と操作を加えて変化する条件とは、同じかどうか？

「何を訳のわからんことをぶつぶつ言ってんだ」とお叱りを受けそうです。が、結構重要なポイントなんです。

統計的に言うと、データは同一母集団であると判断して何もしない、一方、異なる母集団に属しているとみなして対策をとる、ということです。同一母集団であるにもかかわらず異なる母集団に属しているとみなす誤りを第1種の誤り、その反対を第2種の誤りと言っています。

話を戻しますと、同一母集団であると判断して何もしない時は母集団内のバラツキ。同一母集団であるにもかかわらず同一母集団ではないと判断して、何か操作を加えると、そのことが変動要因となって母集団のバラツキが大きくなる。つまり、加えた操作は変動要因となり、バラツキを追加するわけです。第1種の誤りは、余計なことをして事を悪化させることにつながります。

では、この第1種の誤り、あるいはそれに似た誤りは、在庫管理の世界では起きないんでしょうか？　起きるんでしょうか？　起きているとすれば、どんな領域でどれほど頻繁に。