No.112　待ち時間無限大のピークを行ったり来たり・・・

待ち時間は、近似式では稼働率（負荷率）ρが1に近づくに従い急激に長くなり、ρ＝1で∞となります。実際はρが１に近づくと、ある時間ρが１を超えることは頻繁に起きます。待ち時間無限大のピークを行ったり来たりすることになりますが、そのとき、待ち時間はどうなるのでしょうか。調べてみましょう。

１、バラツキがないとき

先ずは、バラツキがまったくないときの状態を確認しておきます。

図１は、処理時間変動係数Cpt＝０、投入間隔変動係数Cti＝０で、工程の処理時間PT＝10、投入間隔Tiを変化させρを0.1～2の間で、投入1番目から50番目までのワークの待ち時間がどのようになるか、近似式で計算した結果を示したものです。

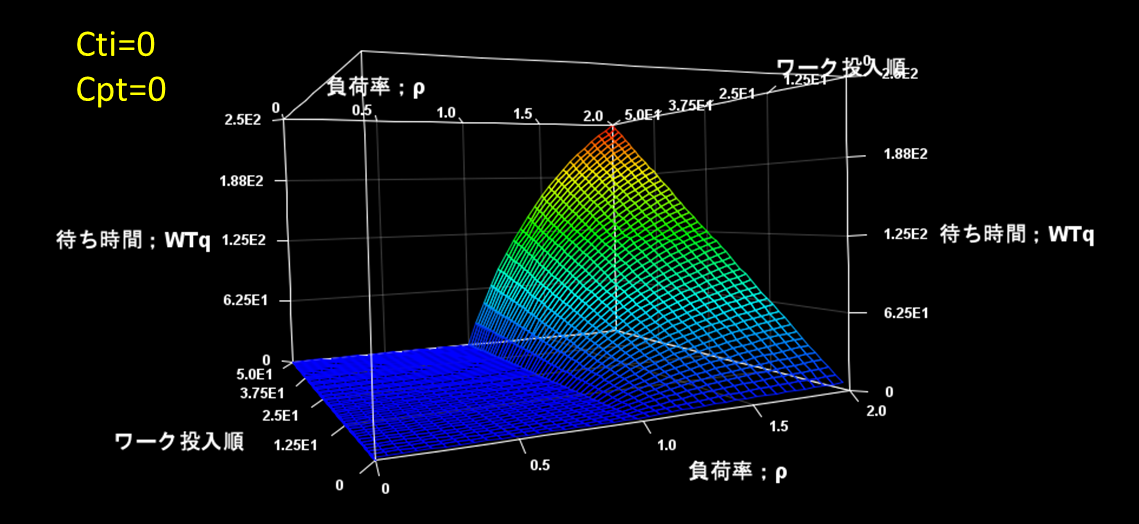
図１　Cti＝0、Cpt＝0で0.1＜ρ＜2での待ち時間

目に付く特徴の一つは、負荷率が1を超える領域で、時間経過（ワーク投入順）とともに待ち時間が長くなり、負荷率が大きくなるに従い待ち時間の長くなるスピードが増すことです。

二つ目は、Cti＝0、Cpt＝0では、ρ＝1でも待ち時間はゼロです。前述した近似式では、Cti≠0やCpt≠0のときはρ＝1で待ち時間は ∞ となりました。[Cti≠0] and/or [Cpt≠0]では∞、 [Cti＝0] and [Cpt＝0]ではゼロ。無限大とゼロが隣り合わせ。

ρって、稼働率とか負荷率とかですが、生産ラインでは、100％がベストと考えることが多く、そこを目指して日夜、努力している工場が大半。ところが、Cti＝0、Cpt＝0というケースは稀です。バラツクのが普通です。CtiやCptがバラツクと稼働率も一定の状態ではなくなります。仮に、平均稼働率が100％だとしても短時間でみた稼働率は100％を境に行ったり来たりすることになります。

２、バラツキがある場合

では、Cti、Cptが変動し、稼働率が100％を行ったり来たりすると待ち時間はどうなるかを調べてみましょう。

２.１　Cti=0、Cpt=0.25の時

待ち時間がどうなるか、エクセルで計算してみました。その一例を図2に示します。

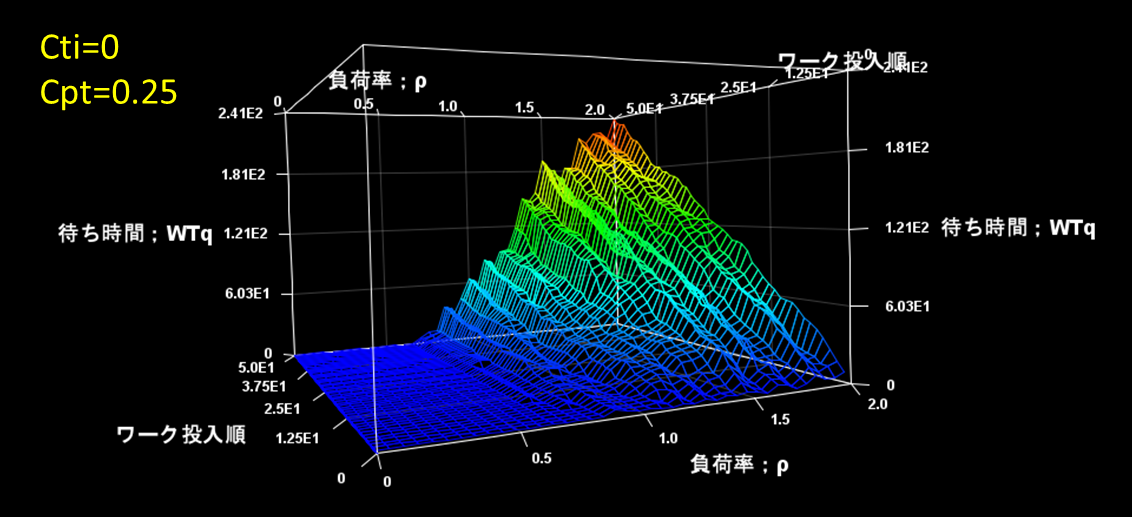
図２　Cti＝0、Cpt＝0.25で0.1＜ρ＜2での待ち時間

図２ですぐ気が付くことは、ギザギザしていることですが、一つ目の特徴である時間経過（ワーク投入順）とともに、また負荷率が大きくなるに従い待ち時間が長くなる、という特徴は同じようです。

二つ目の特徴はどうでしょうか。Cti＝0、Cpt＝0では、いくら時間経過してもρ＝1では待ち時間はゼロですが、Cti＝0、Cpt＝0.25では、ゼロではなくなります。ρ＜1でも待ち時間が発生します。待ち時間の長さの変化は、Cti＝0、Cpt＝0のときの特徴（時間経過とともに長くなる）を維持しているようです。

２.２　Cti＝0のままでCpt＝0.5、0.75、1のとき

Cti＝0のままでCpt＝0.5にしてみます。計算結果を図３に示します。

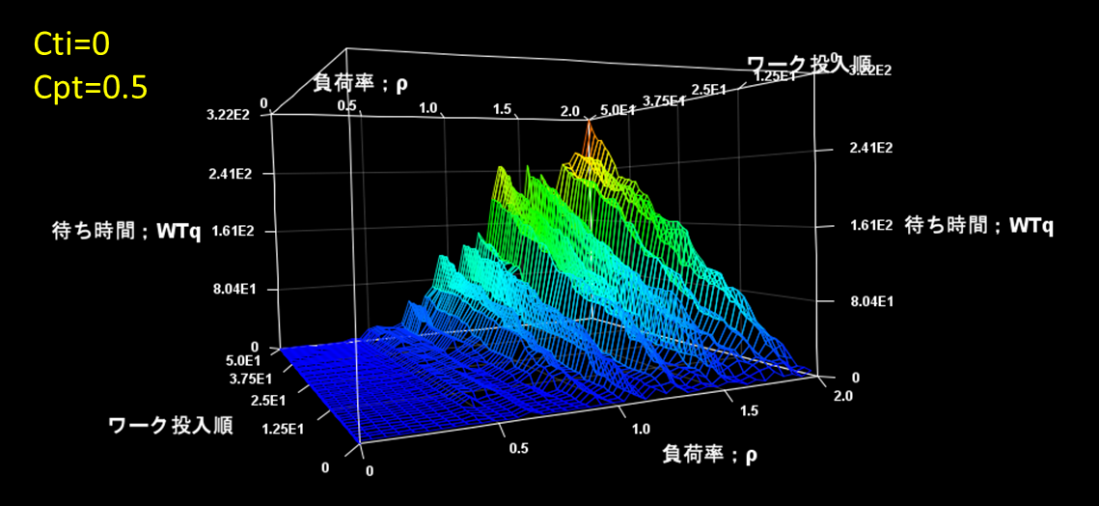
図３　Cti＝0、Cpt＝0.5で0.1＜ρ＜2での待ち時間

図４は、Cti＝0、Cpt＝0.75での待ち時間です。

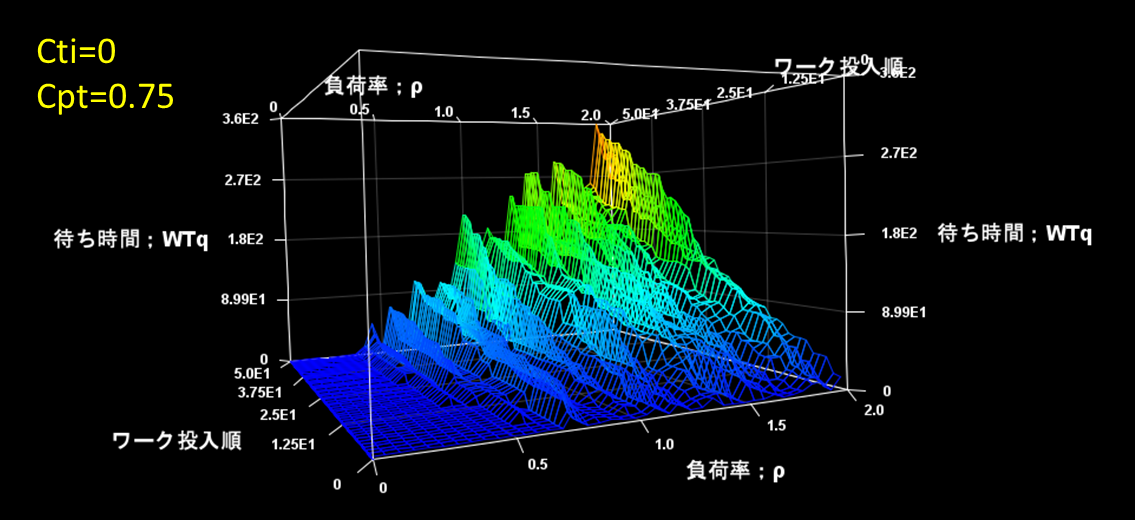
図４　Cti＝0、Cpt＝0.75で0.1＜ρ＜2での待ち時間

図５は、Cti＝0、Cpt＝1での待ち時間です。

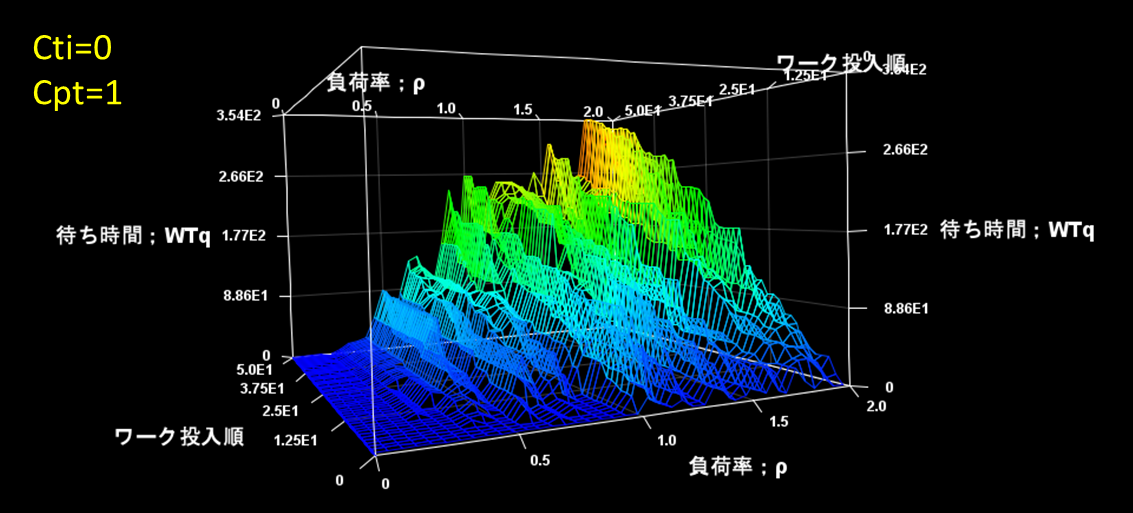
図５　Cti＝0、Cpt＝1で0.1＜ρ＜2での待ち時間

３　ρ＝1近辺の待ち時間の時系列変化

３.１　待ち時間がピーク（ ∞ ）となる稼働率100％（ρ＝1）近辺を計算で確認

ρ＝1と設定しても、投入間隔と処理時間は互いに独立して変動しますから、稼働率100％をまたいで行ったり来たりします。その時、待ち時間がどうなるかを計算してみます。

ワークの投入間隔を10（分）一定として、処理時間平均を10分、変動係数Cptを0.25、0.5、1の3つの条件で、ワークの投入順に1000個のワークごとの待ち時間を、乱数を用いて計算してみます。計算は、各条件それぞれ5回行いました。結果を図６～図８に示します。

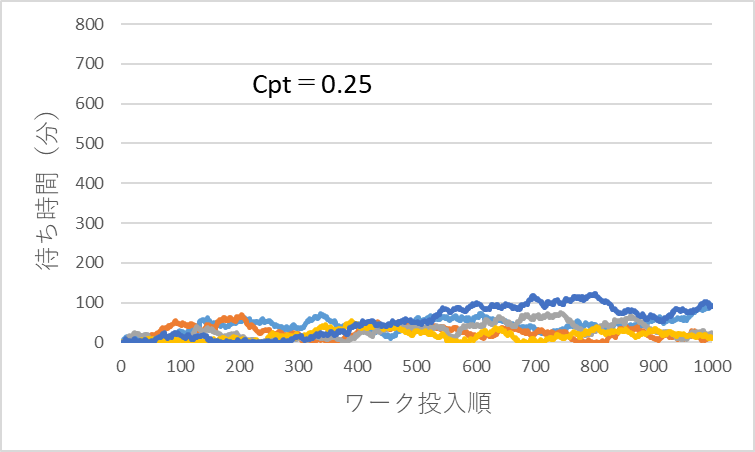
図６　Cpt＝0.25での待ち時間の時系列変化

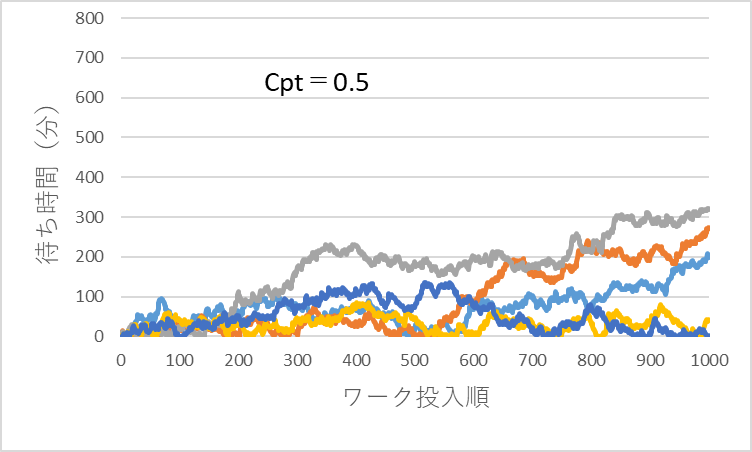
図７　Cpt＝0.5での待ち時間の時系列変化

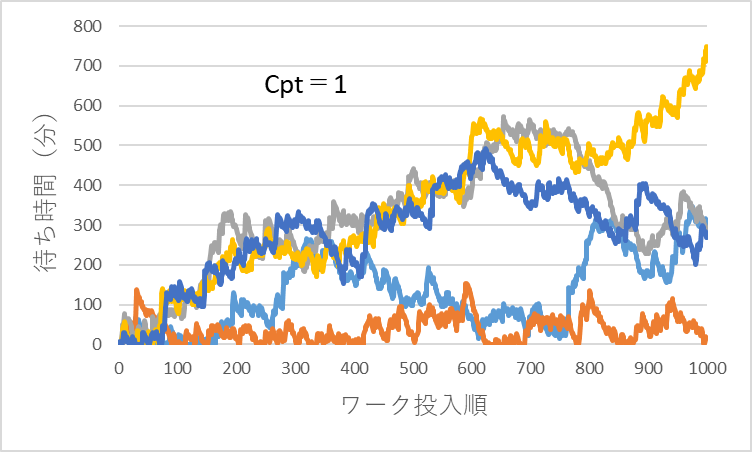
図８　Cpt＝1での待ち時間の時系列変化

特徴としては、
*投入順が後になるほど（時間が経過するほど）待ち時間が長くなる傾向がある
*処理時間のバラツキが大きくなるほど待ち時間は長くなる
*10，000分（6.9日）経過しても待ち時間は長くなり続けている
　注記） 投入1,000番目＝10分×1000番目＝10，000分（166.7時間、6.9日）
*計算ごとに結果は大きく異なる

３.２　考察

計算結果をみるとCptが大きくなるに従い、待ち時間のバラツキが大きくなり、ρ＜1の領域でも待ち時間が発生することがわかります。

Cti=0のままCptだけを大きくしてみましたが、同時にCtiの値も大きくすれば、待ち時間はさらに大きくなると推測できます。

また、計算ごとに、ギザギザの状態や経過時間に対する待ち時間の変化は異なります。

待ち行列理論の平均待ち時間の近似式では、ρ＝1のとき、待ち時間の平均は ∞ となり、現実的な意味はなくなりますので、数式の適用範囲は 0≤ρ＜1 だということになります。しかし現実は、ρ＝1を行ったり来たりしますので、その場合、待ち時間はどうなるの？、という素朴な疑問が湧いてきます。得られた計算結果から、実際起きている現象を思い描いてみたいと思います。

始めに、待ち行列理論で平均待ち時間を求める式の条件を確認しておきます。それは定常状態を条件としていることです。定常状態とは、十分に時間が経過した後に一定値に収束し、その後は変化しなくなるような状態です。

先ず、投入間隔および処理時間がバラツクとき、それぞれが定常状態になるかどうか、、、。ならない感じがしますが、一応、定常状態になる、と仮定してみましょう。次に、両者は互いに独立に変動することを考慮してみます。稼働率は投入間隔に対する処理時間の比ですので、ある期間の両者の比が常に一定ということは、、ないでしょうね。つまり、稼働率が定常状態になることは、ないのではないか、と考えられるわけです。

結果を示す図から、ρ＝1を超えた瞬間に待ち時間が ∞ になるということではない、ことは察しがつきます。大雑把に言えば、ρ＞１の状態のときは待ち時間が時間経過とともに長くなり、ρ＜１のときは時間経過とともに短くなる、ということを繰り返しているものと考えられます。但し、ρ＞１のときは、待ち時間は確実に長くなりますが、ρ＜１のときはある確率で短くなる、ということだと思います。

もうひとつ、重要なことがあります。待ち時間がどれぐらいバラツクか（数学的にいえば分散）を簡単に求める実用的な数式がないんです。分布形状限定の近似式はあるようですが、難解な式が多く、現場では使えそうにありません。計算結果をみても、計算ごとに時系列変化が異なり、実用的な時間で収束する気配もなく、統計的手法も簡単には使えないように思われます。

３.３　シミュレータを使ってシミュレーションしてみる

待ち時間の分布形状がどうなるかはシミュレータでみることができます。待ち行列理論をベースにしたシミュレータは、いくつか市販されています。私は SIMUL8 を使っています。シミュレーションを行うときは乱数を使いますが、乱数も何種類かあり、使う乱数によって結果がかなり違うんです。同じ乱数を使えばまったく同じ結果が出ますが、これはシミュレータが同じ乱数を発生させる機能があるからです。この方が分析するのには便利だと説明されています。

ここで図示したものはエクセルで計算した結果ですが、乱数を使っていますので、簡易的なシミュレーションといってもいいと思います。エクセルの場合は毎回異なる乱数が出て来ますので、シミュレーションを行うごとに結果は大きく異なります。

待ち時間が ∞ をまたいで行ったり来たりするとき、時間経過とともに、限りなく ∞ 近づくということはわかりましたが、その経過を事前に予測することができるかというと、難しい、、、いや、ほとんど不可能でしょうね。

ただ、CptやCtiが小さく、稼働率が低い（60％以下ぐらい？）時は、バラツキもそれほど大きくありませんし、分布形状も比較的安定していますので、シミュレーション結果を用いて管理の枠組みをつくることができる可能性はあるかもしれません。

逆に、多品種変量で受注生産環境では、CptやCtiが大きくなりやすく、稼働率を高く（80％以上とか？）維持しようとすると、待ち時間は予測不能状態になり、管理の混乱を招く要因になることもあるのではないかと危惧されます。

４、とりあえず、まとめ

待ち時間が無限大のピークを行ったり来たりするとき、どんなことが起きているのか、調べてみました。

工程に到着する時間間隔の変動係数（Cti）や工程の処理時間の変動係数（Cpt）が大きくなると、稼働率が高い領域では、短期間ではありますが、ときどき、到着間隔＜処理時間（稼働率が100％以上）になります。つまり、待ち時間が ∞ のピークを行ったり来たりします。

この状態では、時間経過とともに待ち時間は長くなります。但し、長くなる経過はバラバラで再現性はないようです。微視的にみますと、稼働率が100％を超えているときは待ち時間が確実に長くなりますが、100％未満になったからといって急に短くはなりません。例えば稼働率が90％だとしたら、90％の確率で工程はビジーですから、待つ確率の方がはるかに高い、逆にみれば、待ち時間が短くなる確率は低いので、簡単に待ち時間が短くはならないのではないか、と思われます。

生産現場が長い方は、「仕掛が増えるのはあっという間だが、減るのは時間がかかるし、減らそうとしてもなかなか減らない」といったことを経験されていると思います。背後で、稼働率が100％を行ったり来たりしている、のかもしれません。

そのような状態をシミュレーションである程度、確認することはできますが、具体的に実用可能な数値で推定することは困難であると思われます。

このような待ち行列現象が起こりやすい生産現場とは、この現象の発生メカニズムからも推察されますように、生産ラインの投入間隔と各工程の処理時間のバラツキが大きい現場です。ひらたくいえば、多品種変量で受注生産環境にある生産現場。

その大部分は、中小企業ではないでしょうか。もちろん、大企業の中にもそのような企業はありますし、中小企業の中にも自動化、整流化が進んだ企業もありますので、ザックリと言えば、でのことではありますが、、。

経済産業省 商工業実態基本調査によると、日本の中小の製造企業数は製造業全体の99.5％の66万社、大企業は4千社だそうです。中小と大企業の区別が多少曖昧だとしても、日本の製造企業の大部分が多品種変量で受注生産環境にある、といってもいいのではないかと思われます。

日夜、生産性改善に奮闘するも、納期遵守率の改善、仕掛在庫削減は一向に進まない現場。さまざまな改善活動をやってきたが、一時的に効果が出たようにみえても、すぐに元の混乱状態に戻ってしまう現場。２０年も、３０年も前から同じような改善テーマを掲げているが、何も変わっていない現場。生産改善コンサルに聞けば、「管理レベルが低いからだ」といわれて、途方にくれてしまう現場・・・。

そのような生産現場では、無限大のピークを行ったり来たりしているかもしれません。これまでの生産管理で、待ち行列現象なんていう話、ほとんど聞いたことがなかったのではないでしょうか。

「待ち行列現象」という視点から、生産現場を見なおしてみることで、改善のきっかけがつかめるかもしれません。