No.111　稼働率が100％に近づくと、、、待ち時間はどうなる？

前回、生産ラインを流れるワーク（被処理物）が工程前で待つ時間と「トヨタ生産方式」との関係をみてみました。待つ時間の平均（WTｑ）は、
＊投入間隔（平均；Ti、変動係数；Cti）と
＊処理時間（平均；PT、変動係数；Cpt）
で決まる、ということがわかりました。そして、稼働率ρ（＝PT/Ti）100％を狙う「トヨタ生産方式」が成立する条件は、Cti＝0およびCpt＝0（ここでは限りなく0に近づけるという意味を含みます）。

ということで、「トヨタ生産方式」でおなじみの、
＊平準化
＊サイクルタイムでの同期生産
＊作業の標準化
・・・・・
などは、Cti＝0およびCpt＝0を実現するための具体的な方策だ、ということがわかります。

あっ、ひとつ、忘れていました。「トヨタ生産方式」って、予め、つくる“もの”を決めておかなければなりません。つまり、見込生産が条件だ、ということです。買い手が決まる前に生産を始めるという見込生産の条件を曖昧にすると、“変なバラツキ”が発生して、平準化も同期生産もうまくいかなくなります。

一般の企業で「トヨタ生産方式」を再現することは、実は非常に難しい。投入間隔の変動もなし（Cti＝0）、処理時間の変動もなし（Cpt＝0）、ですよ。そんなこと簡単にはできませんよね。お察し頂ければ、と思います。

では、どうするか、、、。少なくとも、言えることは、Cti≠0、Cpt≠0　の条件を許容しなければならない、つまり“バラツキ”を許容しなければならない、ということではないでしょうか。

Cti≠0、Cpt≠0の条件下では、ワークが工程の前で待つ時間が発生します。その時間分だけ生産リードタイムは長くなります。稼働率ρが高くなれば急激に待ち時間は長くなり、稼働率向上のメリットは帳消しとなります。そのような特性を許容し、それと共存しながら生産を管理しなければならない、ということです。

正直、かなりの難題です。・・・ですが、“物は考えよう”。突破口はあるかもしれません。

こんな経験をした方も多いのではないでしょうか。
＊注文が増えると納期も長くなる
＊仕掛削減活動で減った仕掛、いつの間にか元通り
＊生産スケジューラ、現場で使いものならず
＊納期遵守率、改善活動の成果も長続きせず、、
・・・・・
これらは、生産ラインでの待ち行列現象が多かれ少なかれ、影響しています。今始まったことではなく、昔からありました。ただ、待ち行列現象に起因することだ、と理解している人は、ほぼ、皆無。（欧米ではとっくの昔に知られていることですが、、）

これまで、生産現場の混乱は、管理レベルの低さが背景にある、と言われてきました。管理レベルを上げる努力は昔から行われてきました。IT技術も格段に進歩しました。しかし生産管理の問題は、30年前と同じ。なんの進歩もありません。

日本の製造業、停滞の30年の要因とはコレコレだ、と軽々にいうことはできません。商品の多様化、技術の進歩、政治・経済情勢などなど、把握しきれない様々な事柄が関係していることでしょう。ただ、生産ラインの最も基本的なメカニズムについての理解が欠けていたことが、またそのことが認識されていないことが相乗効果となり、思いのほか大きな影響を及ぼしているのではないか、と考えられます。

ということで、投入間隔Tiや処理時間PTにバラツキがある場合、稼働率ρが高い領域で待ち時間WTｑがどのような振る舞いを見せるのか、詳しくみていきたいと思います。

前回調べたように、待ち時間は稼働率が100％に近づくに従い急激に長くなります。そして、ρ＝1では待ち時間平均は∞に発散してしまいます。これは近似式から導き出される挙動ですが、実際∞なんていう値はありませんので、現実とは、かなり違うような感じがします。

待ち時間倍率（WTｒ）の近似式とその３Ｄグラフを再掲します。

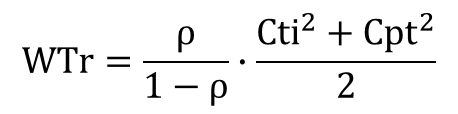
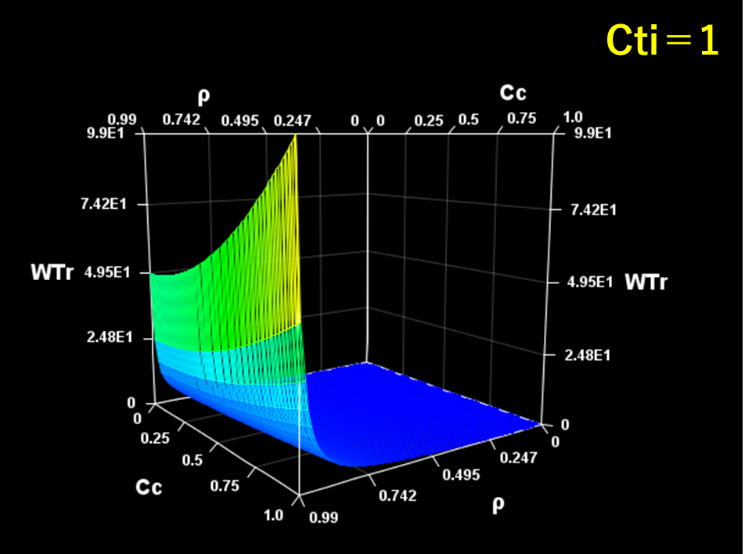
図１　Cti＝1でのＷＴｒ（待ち時間倍率）の特性

特徴は、ρ＝0.8ぐらいからWTｒが急激に上昇することです。そして、式１からもわかりますように、ρ＝1ではＷＴｒは∞となり、発散してしまいます。だったら、ρ＝1を超えたらどうなるんでしょうね、、。∞を突っ切って∞の∞に、、、？

ρ＝1を超えることって、実際時々起こります。TiもPTも変動しますので、ρ＝1をまたいで行ったり来たりします。ということは、、、∞をまたいで、行ったり来たり、、？

ρ＝1、つまり、稼働率というか負荷率というか、が100％近辺では、どのような現象が起きているのか、近似式からは読み取れません。

ということで、少し、戻って、ρ＝1近辺のＷＴｑがどうなるのか、調べてみたいと思います。図２を参照ください。

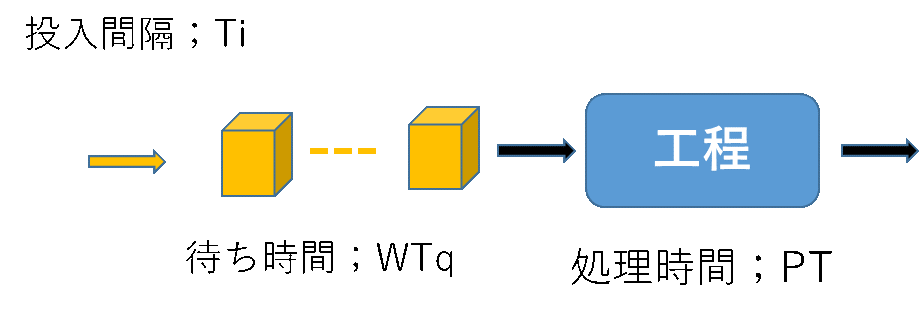
図２　ひとつの工程；投入（到着）間隔Ti、処理時間PT、待ち時間WTｑ

TiもPTもバラツキがないとします。こうするとWTｑの計算が簡単になります。ＰＴ＝10（分）だとします。Ｔｉ＝12（分）ならＷＴｑ＝0となります。では、Ｔｉ＝9（分）なら、、そうですね、工程での処理が終わらないうちにワークが来てしまいますので、待ち時間が発生してしまいます。Ｔｉ＝7（分）なら、、、４（分）なら、、、待つ時間がどんどん長くなります。

一例を図３に示します。PT/Ti＝負荷率　として0～２、投入した順にワークごとの待ち時間を示しています。ワーク投入順に従い時間も経過します。

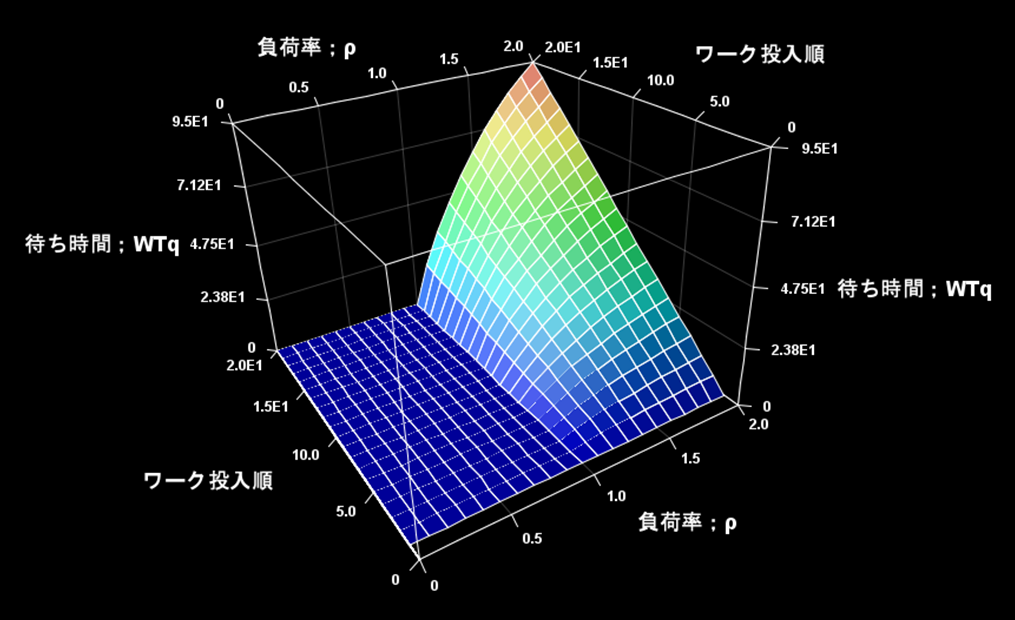
図３　PT=10(分)、ρ；0～2、ワーク投入順；1～20のときのWTｑ

ρ（負荷率）＝0～1の範囲ではWTｑ＝0ですが、ρ＝1を超えるとワーク投入順の2番目のワークから待ち時間が発生します。投入数が増えるに従い（時間が経過するに従い）待ち時間は長くなります。また、ρが高くなるに従いWTｑは長くなります。

図３で、ρ＝1では、時間がいくら経過しても、待ち時間；WTq=0。近似式（式１）では、Cti=0、Cpt=0の時、WTq=0となりますので、図３と一致します。

ところが、Cti≠0 あるいはCpt≠0であれば　ρ/（１－ρ）　が∞となり、WTｑも∞となってしまいますので、近似式は、０≦ρ＜1　の範囲でしか適用できないことがわかります。しかし、実際は、ρが1を超えるときがあり、その時１を通過します。生産ラインでは稼働率をできるだけ高くしようとしますので、そういうことが頻繁に起きます。

近似式ではわからないρが1の時、待ち時間はどうなるのでしょう。次回、ρが1の近辺の動きをもう少し詳しく調べてみたいと思います。