No.100　DBRで見落とされた生産ラインの基本特性　

4工程直列ラインの各工程処理時間がバラツク場合、平均値で予定した完了時刻以内で完成する確率は6.25％だっていう話、DBRの説明にはよく出てくるんですよね。これを正しいと思っている人は結構います。TOCのコンサルタントは全員、正しいって信じ切っているようです。もちろん、これは、正しくありません。

じゃ、何％かというと、バラツキの大きさにもよるんですが、負荷率100％では、ほぼゼロ％、という話を前回しました。

今回は、なぜそうなるのか、そのメカニズムを、シミュレーション結果などを交えて解説してみようと思います。

図１　直列4工程生産ライン

図１をご覧ください。条件を簡単にするため、A～D工程の処理時間の平均は10分、標準偏差は2分の釣鐘状分布形状としましょうか。ワークの投入は在庫から行うことにします。A工程では1番目のワークの処理が終了したら直ちに2番目のワークの処理を始めることができますので、手空き時間はなく、稼働率は100％となります。

A工程の処理時間はバラツキますので、A工程の終了時刻もそれに沿ってバラツキます。このバラツキはB工程への投入時間間隔のバラツキとなります。A工程を終了してB工程に投入される時、B工程が手空き状態であれば、ただちに処理を始めることができます。B工程がビジィー状態（前のワークの処理中）であれば、ワークはB工程の処理が終わるのを待たなければなりません。B→C、C→Dも同様なメカニズムで流れていきます。

つまり、A工程での処理開始からB工程、C工程、D工程と工程ごとに待ち時間と処理時間が加算されていきます。ここでは、工程を流れる時間をフロータイムと呼んでおきます。

フロータイム＝処理時間＋待ち時間

となります。（その他現実では、段取り時間とか、部品不良とか、機械故障とか、、様々な時間が発生しますが、ここでは、生産ラインの原理についての説明ですので省略します）

当然ですが、フロータイムはワークごとにバラツキます。どんなふうにバラツクのか、一例を図２に示します。

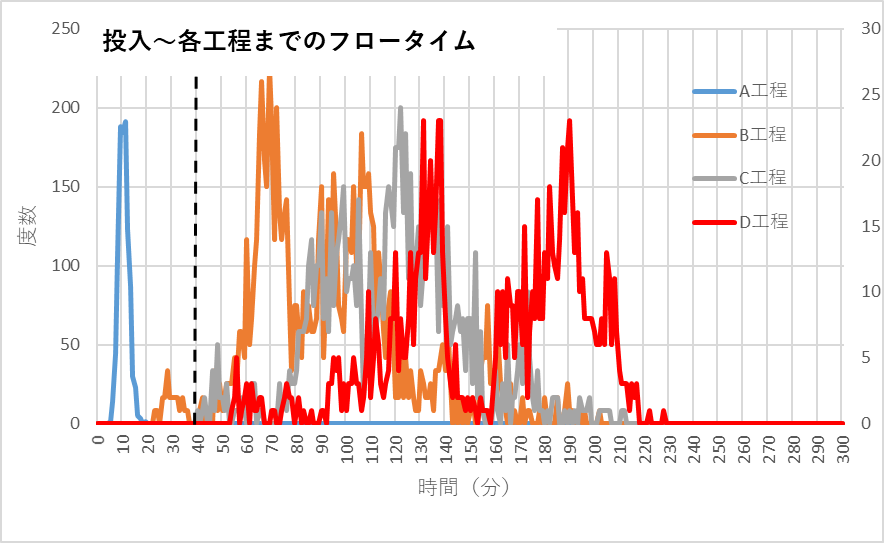
図２　投入から各工程の終了時間の分布の一例

A工程終了時間は、待ち時間はゼロですので処理時間だけで、処理時間の平均10分、標準偏差2分の分布となります。B工程～D工程の終了時間は通過工程の（処理時間＋待ち時間）の累積となり、工程を経るごとに平均、バラツキとも大きくなります。

このようなシミュレーションは市販の生産ライン・シミュレータで簡単に行うことができますが、ここでは、エクセルを用いて行いました。どちらも同じような結果が出ます。

フロータイムの分布形状ですが、正規分布とはかけ離れ、かなりバラついています。さらに始末の悪いことには、この分布形状、シミュレーションを行うごとに、大きく変化します。ですから、分布形状がこうなる、と言い切ることができません。シミュレーション回数を増やして、傾向をみることはできるかもしれませんが、、。

図２の縦破線がD工程の平均終了時間；40分です。実際の終了時間は赤線の分布です。赤線の分布が40分以下の領域にはありませんので、予定時間内に終わる確率は“ゼロ”となっています。必ずゼロとなるわけではありませんが、この条件下ではほとんどの場合ゼロとなります。決して6.25％やその近辺の値ではありません。

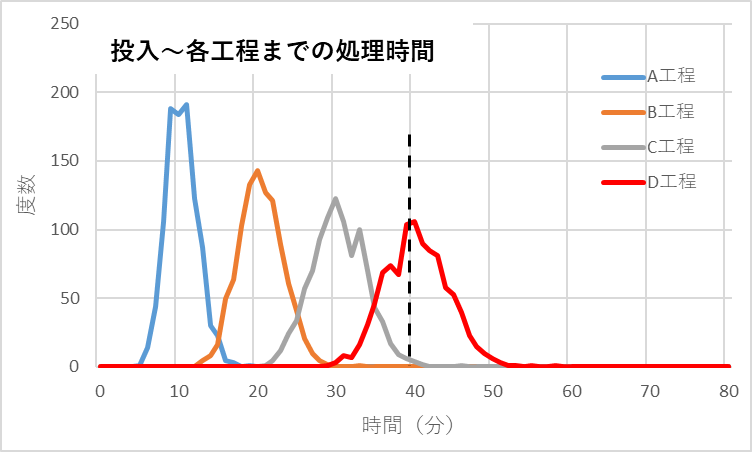
図３　投入～各工程までの処理時間の分布

図３は工程ごとの処理時間の分布です。投入～D工程終了までのフロータイムの平均と標準偏差は次のように計算できます。

平均；10分＋10分＋10分＋10分＝40（分）
標準偏差；　√(2^2+2^2+2^2+2^2 )=4（分）

図２と図３を比べると、フロータイムと処理時間の差が大きいことがわかります。

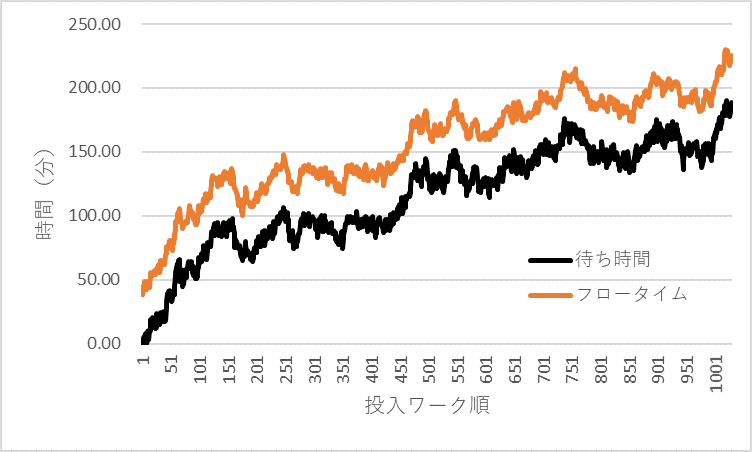
図４　フロータイムと待ち時間の推移の一例

図４は各ワークのフロータイムと待ち時間の推移です。フロータイムに占める待ち時間の比率が大きいことがわかります。また、時間の経過とともに待ち時間とフロータイムが長くなっているのがわかります。理論的には、稼働率100％では、待ち時間もフロータイムも経過時間とともに、無限に長くなります。

ゴール・システム・コンサルティング株式会社のDBR （http://www.goal-consulting.com/solution/s-dbr.html）の説明とはまったく異なることがわかります。このページに、ちょっと違和感のある説明があります。抜粋します。

TOCではまったく違う考え方を取ります。すなわち"早期完了を伝播させる仕組みを作るため"に、能力のアンバランスを「好ましい」ものとして積極的に活用するのです。それぞれの工程を、
l 「遅れ」を発生させる工程と（ボトルネック工程）
l 「進み」を伝播させる（非ボトルネック工程）
に分けて考え、「遅れ」と「進み」の両方が伝播するように組み立てれば、全体を最適にコントロールできると考えるのです。

この説明、わかりにくいんですよね。ここでの「遅れ」の意味は、平均処理時間より長くかかったとき、「進み」は平均処理時間より短いとき、という定義のようです。そして、

“ボトルネック工程は「遅れ」を発生させるが、非ボトルネック工程は「進み」を伝搬させる”

と言ってるように思われます。直列生産工程の特性から言いますと、ボトルネックでも非ボトルネックでも同様に、処理時間、待ち時間が累積されていきます。そして処理時間と待ち時間とは切り離して計算できます。ボトルネックであろうが非ボトルネックであろうが、区別する必要はありません。上記の説明は誤解を招きかねません。

ポイントは、待ち時間です。じゃ、この待ち時間って、どのぐらいなのか、、ですが。最も象徴的な式は、投入時間間隔も処理時間の確率分布も指数分布するとき、

平均待ち時間＝工程の処理時間平均×稼働率÷（１-稼働率）

となります。ボトルネック工程の稼働率は高くなりますので、待ち時間は非常に長くなります。数値を入れて試算してみればすぐにわかります。処理時間平均を10分のとき、稼働率が95％であれば、

平均待ち時間＝10×0.95÷（1-0.95）＝190　（分）＝3.2（時間）

稼働率が99％であれば、

平均待ち時間＝10×0.9÷（1-0.9）＝990　（分）＝16.5（時間）

病院で3時間待って、診察・治療が10分、とか、コロナワクチンの接種で3時間ならんで接種に要した時間は5分足らず、、なんて言いう話と合いますよね。

非ボトルネックでの待ち時間はどうなるかと言いますと、同じ式で、稼働率を換えればＯＫ。稼働率が50％だと、

平均待ち時間＝10×0.5÷（1-0.5）＝10　（分）

70％では、

平均待ち時間＝10×0.7÷（1-0.7）＝23　（分）

稼働率によって待ち時間が大きく変わります。で、「ボトルネック工程」の稼働率って、何％なんでしょうね。「稼働率何％以上がボトルネック、それ以下は非ボトルネック」。　こんな定義、DBRの説明の中ではどこにもありませんよね。

「遅れ」と「進み」の両方が伝播するように組み立てれば、全体を最適にコントロールできると考えるのです。

処理時間は加法性があり、平均、バラツキとも稼働率に関係なく近似計算はできますが、待ち時間は、既述の計算例でも分かるように、稼働率によって大きく左右されます。ボトルネック、非ボトルネックの稼働率の定義もないまま、それらを区別しても、物理的・論理的整合性が取れないのではないでしょうか。それで、生産ラインの全体を最適にコントロールできる、はずはありません。