前回、トヨタの(生産リードタイム/加工時間)比は200~300であるのに対して、普通のメーカーのそれは2,000~3,000、つまり、トヨタの10倍だ、ということを待ち行列理論で説明してみました。ご納得いただければ幸いです。
待ち行列現象は日常、よく見かけます。スーパーのレジ、銀行の窓口、コロナワクチン接種会場などなど、、で。しかし、生産ラインの工程の前にできる仕掛の溜まり具合が待ち行列理論で説明できる、ということはあまり知られていないようです。知らなくてもいいんです。生産ラインの基本特性をきちんと理解できていれば、、。
実際はどうなんでしょうか。生産現場で働く管理者はどの程度生産ラインの基本特性を理解しているのか。生産ラインの基本特性といってもいろいろありますので、ここでは稼働率とリードタイムの関係に絞って考えてみます。
稼働率とリードタイムの関係をきちんと説明できなくても、経験者の多くは、忙しくなると、つまり生産ラインへの投入が増え、稼働率が高くなると、工程内仕掛が多くなりリードタイムが長くなることを知っています。それを理論的に説明はできなくても、経験則は、日常の生産管理を行ううえで役に立っているはずです。生産現場を切り盛りできるようになるまでに結構長い経験(例えば10年以上)が必要だ、という現場が多いのは、そういうことじゃないかと考えられるわけです。
生産管理に関する書籍は多数ありますが、稼働率とリードタイムの関係についての言及はほとんど目にしません。藤本教授の「生産マネジメントⅠ」で待ち行列問題を取り上げていたことに、新鮮ささえ感じました。但し、肝心の「稼働率vsリードタイム(在庫・仕掛)」の説明がないので、少しがっかり。
で、実際、待ち行列理論は生産管理にどの程度役に立つのでしょうか。生産ラインの基本特性を理解するのに役に立ちそうだとしても、現実的にはどうなのか。ということで、少し、斬り込んでみたいと思います。
ただ、私は待ち行列理論についてはまったくのしろうとです。待ち行列理論の解説をするわけではありません。生産現場の管理にどのように利用できるか、を調べてみようというだけのことです
待ち行列理論を生産ラインで使う場合、一番多いのは、工程前の仕掛数がどのように増減するかとか、待ち時間の長さはどのぐらいか、とかでしょう。で、待ち時間にしても仕掛数にしても、待ち行列理論の一般的な本には平均値を求める式しかありません。当然、前工程から流れてくる時間間隔も工程の処理時間もバラツキますので、待ち時間も仕掛数もバラツキます。そのバラツキがどの程度なのか、現場管理者は知りたくなります。
待ち時間分布(Waiting Time Distribution)をWebで調べるとたくさん出てきますが、どれもややこしくて難しそうなものばかり。その中でひとつ、使えそうなのがありましたので引用します。
M/M/1のときに,待ち時間がtよりも長い確率P>tは次の式で表されます。
P>t=ρ・e-(1-ρ)μt
M/M/1はもっとも代表的な待ち行列モデルです。生産工程では、最初のMは前工程から流れてくるワーク(被処理物)の時間間隔が指数分布、次のMは工程の処理時間が指数分布、次の1は工程の数を示します。
上式でμは平均サービス率、生産ラインでは単位時間当たりの処理数、ρは工程の稼働率、tは経過時間を表します。
μ=1、稼働率ρが0.25,0.5,0.7,0.8,0.9のときの「待ち時間vs待ち時間以上待つ確率」を上記の式で求めた一例を図1に示します。待ち時間0の時の待つ確率は稼働率と同じになります。横軸は平均待ち時間を表します。横軸1上の確率は平均待ち時間以上待つ確率です。横軸2は平均時間の2倍を示し、その時間以上待つ確率を示します。稼働率90%では平均待ち時間以上待つ確率が約80%、平均待ち時間の5倍以上待つ確率が50%強、10倍以上待つ確率が30%強ある、ということです。稼働率50%でも平均待ち時間の3倍以上待つ確率が10%程度である、ことになります。
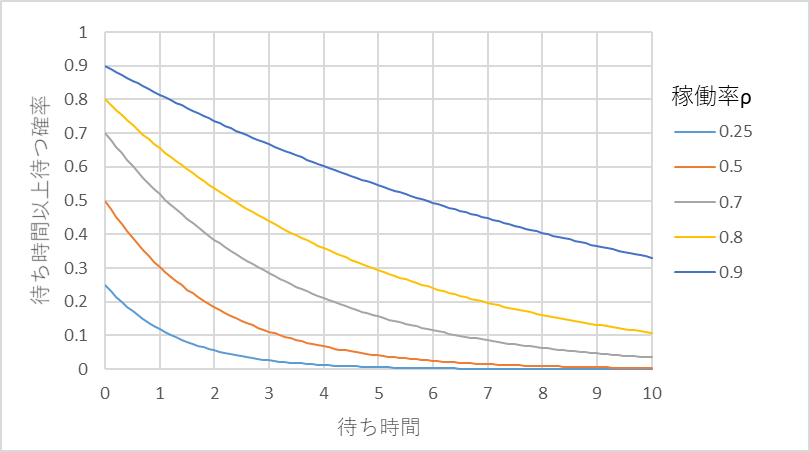
図1 待ち時間vs待ち時間以上待つ確率
非常に広い分布だ、ということはおわかりいただけると思いますが、最もよく使われる正規分布の広がり具合と比べるとより実感できるのではないかと思います。図2に平均0、標準偏差1の正規分布を示します。赤線は(1-累積確率)を示します。
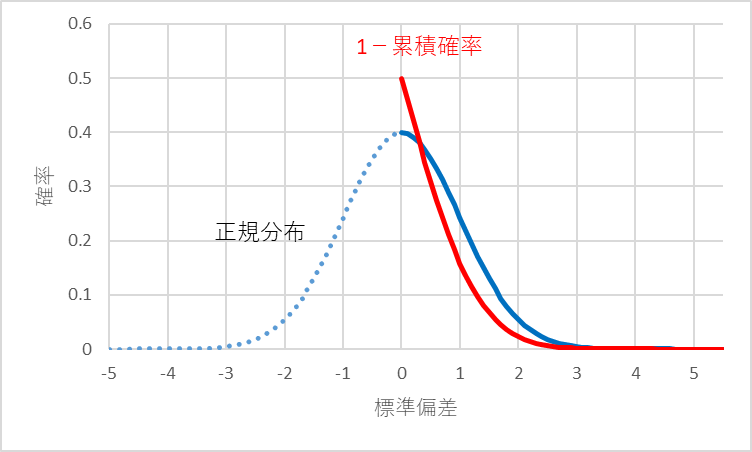
図2 正規分布、平均0、標準偏差1、赤線は(1-累積確率)
図1の待ち時間の分布に図2の正規分布の赤線を重ねたものを図3に示します。正規分布の広がりと比べると待ち時間の分布の広がりの大きさを感じていただけると思います。但しこの比較の数理的な意味については不問としてください。感覚的に待ち時間の分布の広さを感じていただくためのものですので、、。
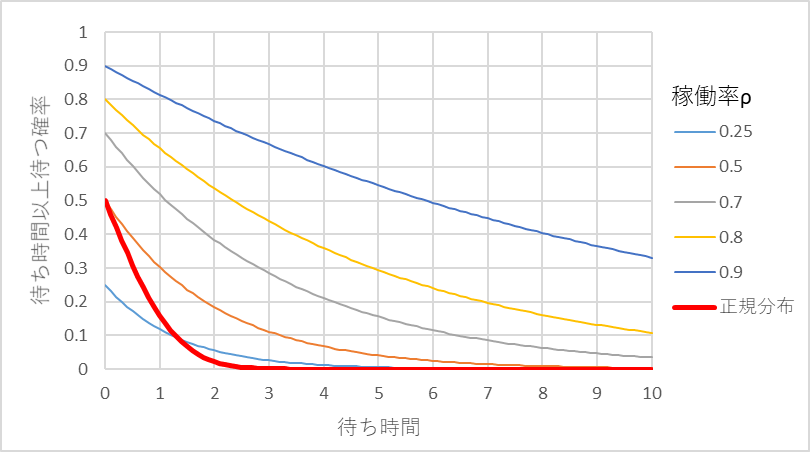
図3 正規分布と待ち時間分布の比較
この数式には隠れた変数がもうひとつあります。それは、
平均到着率;λ
で、単位時間当り処理数です。μ、λ、ρの関係は次のようになります。
ρ=λ/μ
ここで、確認しておきたいことは、μもλも平均値です。従ってρも平均値です。待ち時間;WTも平均待ち時間として次の式で求められます。
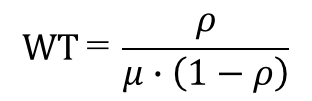
つまり、μ、λ、ρ、WTすべてが平均値です。これは、待ち行列モデルはμ、λ、ρはそれぞれ平均値で、時間とともに変化しない定常状態を条件としています。μ、λそれぞれは独立に変動しますのでρも時間経過とともに変動しますが、平均は一定という状態です。
現実的にこのような状態が存在するかといいますと、多分、ほとんどないでしょう。
もっともよく使われる待ち行列モデルはM/M/1ですが、到着時間間隔も処理時間も指数分布に従う生産工程なんて、まず、ないでしょう。指数分布以外にもアーラン分布、一般分布(平均と分散を指定)、一定分布などもありますが、これらのモデルで待ち時間の分布を求める実用的な数式があるモデルはありません。
ここで検討した待ち時間の分布は、現実的にはありえない特殊な条件でのことです。仮に、実際の状態がその特殊な条件に近いとしても、今度は待ち時間の分布が広すぎるため予測精度が低くなり、使えません。ということで、実際に待ち行列理論を生産ラインの管理や分析に使うことは、ほとんどありません。
それから稼働率なんですが、これもわかりづらい。稼働率って、ある時間間隔の中で、稼働可能時間に対する付加価値稼働時間の比です。観測時間間隔が長ければ比較的安定した稼働率が得られますが、観測時間間隔が短くなってくるとバラツキが大きくなってきます。
8:00~9:00の稼働率は0、9:00~10:00の稼働率は95%、、、なんていうことになります。3割バッターが3試合連続ノーヒット、1割台のバッターが3試合続けて猛打賞なんていう話と似ています。
待ち時間は稼働率が高い領域では特に、稼働率に対して敏感に反応しますが、一方で稼働率として計測されるまでの時間遅れがありますので、それを考慮すると非常に使い難くなります。
というように、待ち行列理論を生産ラインに応用するのは結構大変です。だから、あまり利用されていないんじゃないか、と思うわけです。