藤本教授は待ち行列問題の基本構造が在庫問題のそれと似ていると切り出し、在庫問題と待ち行列問題の関連性を説明していますが、
*対トヨタ生産期間比10倍の差を解消できるか?
*連結機構なしの工程間仕掛・在庫をどのように管理するのか?
の二つの疑問解消には至っておりません。今回は、この疑問解消につながる道筋発見にチャレンジしてみようと思います。
藤本教授の説明で疑問解消に至らなかった理由は何か、その辺りから見直してみましょう。よくわかりませんが、可能性として考えられるのは、在庫問題vs待ち行列問題というくくりに問題があるように感じます。根拠はありません。直観的に、です。
経験則+直観を頼りに捜索開始。
想定する生産ラインのイメージを図1に示すような構成で考えてみます。工程がいくつか連結されている一つのまとまりをセグメントとします。工程から工程へはFIFO(ファーストイン・ファーストアウト)で流れ、搬送方法・時間は考えないことにします。セグメント間は、セグメントを出た仕掛と次のセグメントへの投入用仕掛があり、何らかの在庫管理が行われているとします。最初のセグメント(生産ラインの投入工程)へは原材料在庫(資材倉庫のような)から直接投入することとします。完成品在庫は含めないことにします。つまり、仕掛・在庫を原材料、工程間、セグメント間の3種類にわけて考えようということです。
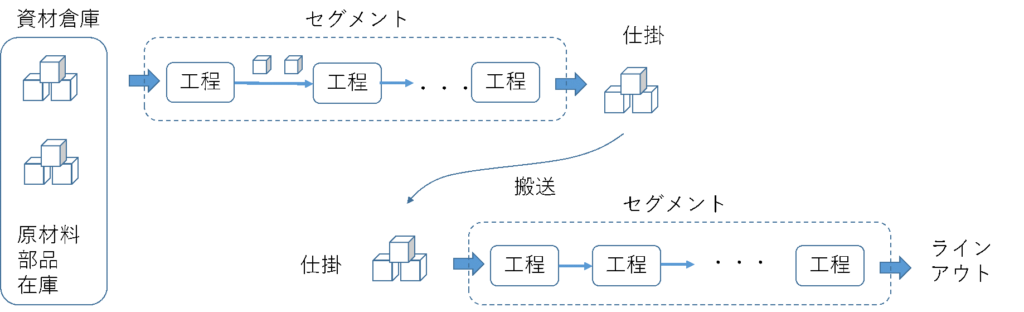
図1 生産ラインのイメージ
こんなイメージを描きながら、待ち行列問題に取り組みます。待ち行列のメカニズムを調べてみましょう。藤本教授が示した数式を使うことにします。行列で待つ時間(平均行列時間)と客数(平均行列長)は次の式で求められます。

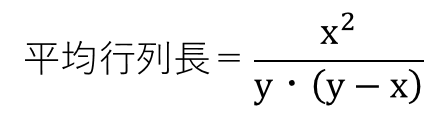
(xはポアッソン分布、yは指数分布とする)
用語、記号の意味を確認しておきます。
x=平均到着率;単位時間あたりに到着する客数
y=平均サービス率;単位時間内にサービスをする客数
平均行列時間;一人の客が行列で待つ時間の平均
平均行列長;行列にいる客数の平均
具体的な事例で考えてみます。
ある銀行の窓口でのサービス時間は一人平均6分。営業時間は8時間で来客数の平均は64人。単位時間を1時間(60分)とします。平均到着率と平均サービス率は次のようになります。
平均到着率;x=64(人)÷8(時間)=8(人/時間)
平均サービス率;y=60(分)÷6(分/1人)=10(人)
平均行列時間と平均行列長は次のようになります。
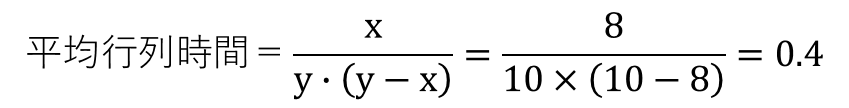
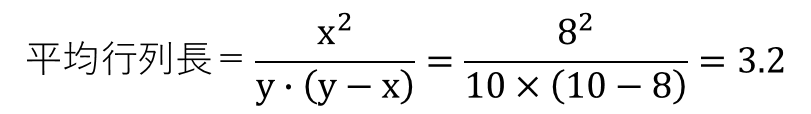
平均行列時間は0.4時間(24分)、平均行列長は3.2人となります。
では、次にサービス時間はそのままで、来客数を1人/時間、2人/時間、、、と変化した時、平均行列時間と平均行列長はどのように変化するかをみてみましょう。計算結果の一例を図2に示します。
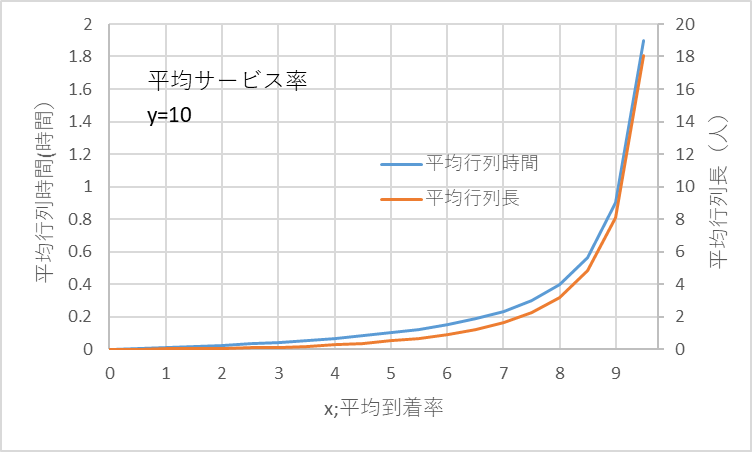
図2 平均到着率に対する平均行列時間と平均行列長
図2をみてわかりますように、平均到着率;xが高くなると、ここでは1時間当たりの来客数が多くなると、平均行列時間も平均行列長も指数関数的に急激に長くなります。xが7人のとき平均行列時間は0.23時間(14分)、平均行列長は1.63人ですが、xが9人になるとそれぞれ、0.9時間(54分)、8.1人と急増します。
平均到着率と平均サービス率を別々に捉えていますが、平均サービス率に対する平均到着率の比で捉える方が便利で、一般的です。この比は窓口(サービス施設)の稼働可能時間に対するサービス時間の比になりますので、窓口利用率などと呼ばれております。生産ラインでは工程の稼働率に相当します。

つまり、工程の稼働率が高くなると平均行列時間も平均行列長も指数関数的に急激に長くなる、ということになります。但し、平均到着率<平均サービス率 の範囲です。平均到着率≧平均サービス率 では平均行列時間も平均行列長も時間の経過とともに無限大まで長くなり続けます。
行列時間も行列長も平均を求める式しかありません。バラツキはどうなるか、分散とか標準偏差を求める式ってあるか、探してみましたが使えそうなものは見つかりません。探し方が悪かったんでしょうか。ご存知の方がおりましたら、ご教示頂ければ助かります。
シミュレーションでおおよその性質はわかります。行列時間も行列長も短いうちはいいのですが、グーンと長くなる辺りからバラツキも急激に大きくなり、分布形状はだだっ広い丘陵状になります。ということは、どの程度のバラツキがあるのかもよくわからないことが多い、ということになります。
このような特性を頭に置きながら、生産ラインのイメージ図に戻ります。
仕掛・在庫の存在は、外部から納入される原材料・部品在庫、工程間の仕掛、セグメント間の仕掛の3種類としました。この3つの中のどれが一番、一般の待ち行列に近いでしょうか? 原材料・部品在庫もセグメント間仕掛も在庫の出入りだけで、サービス施設を含んでいませんが、工程間仕掛は工程というサービス施設を含んでおります。工程間仕掛と一般の待ち行列の基本構造が同じであると考えられます。図3を参照ください。
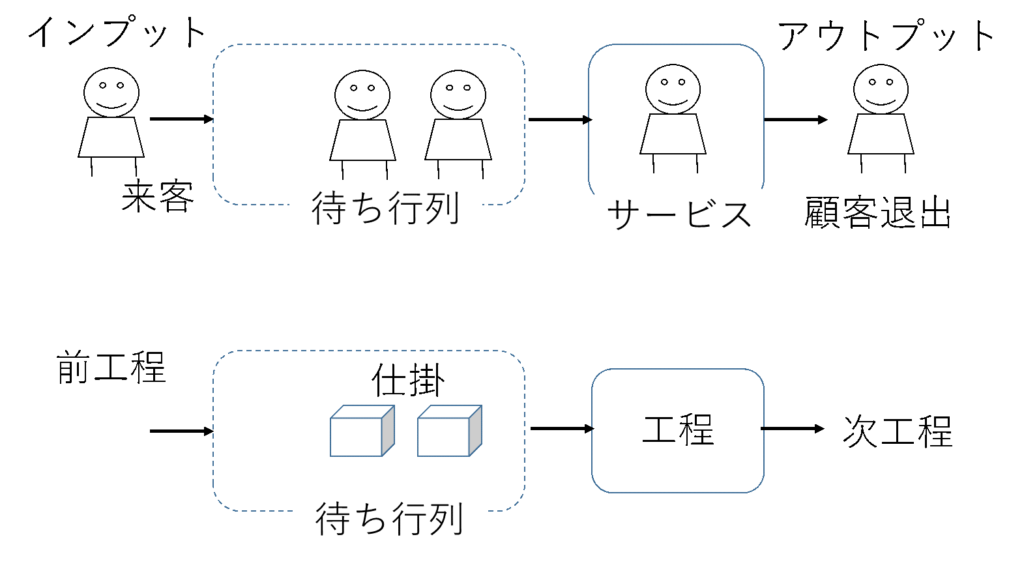
図3 一般の待ち行列(上)と工程間の待ち行列(下)
先に行った試算事例を工程に置き換えると次のようになります。
工程平均処理時間(1/x);6分
前工程からの到着時間間隔(1/y);8分
平均待ち時間;24分
平均仕掛数;3.2個
藤本教授の説明は、EOQや安全在庫などの在庫問題に待ち行列問題を適用しようとしたことが間違いだった、ということになりそうです。持ち行列問題は工程間仕掛の分析に使えば良かった、ということじゃないでしょうか。
藤本教授は次のように説明しています。
・・・正味作業時間:生産期間、トヨタは1:200、普通のメーカーは1:2000。つまり、普通のメーカーの正味作業時間に対する生産期間はトヨタの10倍である・・・
普通のメーカーは生産性を高めるため稼働率をできるだけ高くしようとします。そうしますと行列時間(待ち時間)や行列長(仕掛数)が急激に増大し、正味作業時間の数倍、バラツキを考慮すれば10倍以上になることもありえるのではないでしょうか。
「普通のメーカーの正味作業時間に対する生産期間はトヨタの10倍である」という実態を待ち行列現象で説明できる、と考えるわけです。
*対トヨタ生産期間比10倍の差を解消できるか?
*連結機構なしの工程間仕掛・在庫をどのように管理するのか?
まだ、二つの疑問に対する具体的な解決策が見つかったわけではありません。しかし、「在庫問題」から「工程間仕掛の挙動」に視点をずらすことで、待ち行列現象との因果関係が鮮明に浮かび上がってきました。これで、解決への方向が見えてくるのではないでしょうか。