現場改善会計論(以下、GKC)の“オソマツさ”は、半端じゃありません。なぜ、こんな論文が学会から賞を授与されたのか、理解不能です。こうなると、論文そのものよりも、その背後にある「何か」に関心が向いてしまいます。前にも、「ブログ;現場改善会計論の裏側を覗いてみると、、」で、GKCの背後をみてみましたが、その時は、論理の筋を追いながらあっちに行ったり、こっちに来たりしているうちに、裏口に迷い込んだっていう感じでした。で、今回は意識的に、裏側に光を当ててみようか、と。
GKC関連の論文等を読んで感じることは、本件にかかわる3教授(藤本隆宏、上總康行、柊紫乃)の専門知識レベルの低劣さです。「いかなる経済状況下でも、改善効果を貨幣的に測定できる」とする “しろうと理論” を自信満々に展開する「図々しさ」はどこから来るのか。
それを知る手掛かりは、生産ラインの基本的物理特性を記述するうえで重要な「時間」を彼らはどのように理解、解釈しているのか、そのあたりにありそうだ。ということで今回は、
「製造現場における改善効果測定と2種類の時間概念」柊紫乃、上總康行、2017
にスポットライトを当ててみようと思います。
1、「2種類の時間概念」から探る3教授の時間概念
生産ラインの特性でもっとも重要な次元である「時間」についてGKCはどのように捉えているのか、「製造現場における改善効果測定と2種類の時間概念」(以下、「2種時間概念」と略称)が手がかりになりそうだ。
製造現場で使う時間は、被処理物(以降、ワーク)の加工や組立時間(以下、処理時間)、ワークの待ち時間(以下、待ち時間)、工程がワークの到着を待つ時間(以下、手空き時間)、生産ラインへの投入から完成までの時間(以下、生産リードタイム)等々、ある。「2種時間概念」では「作業時間」と「リードタイム」の2種類に分類し、GKCの理論構築のベース(土台)にしようとしているように思われる。
だが、「2種時間概念」を読んだだけでは、GKCが生産ラインにおける「時間」をどのように捉えているのか、評価しにくい。世の中の雑多な常識的ノイズが多いからだ。そこで先ず、すでに知られている関連知見、理論等の中でもっとも関連が深いと思われる理論を紹介する。それを拠り所として「2種時間概念」とGKCの関係を解きほぐしてみたい。
2、生産ラインの時間特性と「待ち行列理論」
生産ラインの時間に関する理論として利用されているのが「待ち行列理論」である。「待ち行列理論」は20世紀の初めに電話交換機の必要台数を計算するために考え出されたものだが、現在では、情報通信、計算機などのネットワークなどに幅広く使われている。在庫、生産システムの設計や運用に関しても、1980年代以後、製造業の復権をめざす米国を中心に「待ち行列理論」を駆使した理論的研究が精力的に行われてきた。
しかし、一見すると簡単な構造にみえる生産ラインだが、不確定要因がある偶然現象を内在しているために、統計理論も限定的にしか使えない。「待ち行列理論」で生産ラインのメカニズムを記述できる範囲は限られていることに留意する必要がある。
偶然現象を再現する方法としてシミュレーションがある。生産ラインの条件を設定すれば、工程ごとの処理時間、待ち時間、手空き時間そして生産リードタイムなどなど、結果は得られる。それぞれの平均値や分布形状もわかる。ところが、処理時間以外の待ち時間、手空き時間、生産リードタイムについては、それらの分布形状が右肩下がりでだだっ広く、統計理論で確率計算しても実用的な解をみつけることは難しいのである。
「待ち行列理論」も、その数理モデルやシミュレーションも万全ではないが、生産ラインの特性を時間という切り口で理解するうえでは有用である。作業時間とリードタイムの関係を、GKCはどのように理論構成の土台に使ったのか、の解析にも役に立つのではないか。
先ず、「待ち行列理論」を使って、生産ラインの基本特性を記述してみる。
2.1 「処理時間」と「生産リードタイム」の関係を「待ち行列理論」で解析
生産ラインの物理的、工学的特性を「待ち行列理論」を応用して解析してみる。先ず、図1に示す生産ラインをモデルに、用語、記号を整理しておく。
「2種時間概念」では「直接作業時間」としているが、ここでは、工程での処理が開始してから終了するまでの時間を「処理時間」とし、記号はTpとする。「処理時間」は、その工程の生産能力を占有している時間と考え、「ムダ時間等」を含む。生産ラインに投入されてから完成するまでの時間を「生産リードタイム」とし、記号はLTとする。投入や前工程から流れてくるワークの時間間隔をTi、工程前でワークが待つ時間をWT、工程が手空き(手待ち)になる時間をFrTとする。

図1 5工程生産ライン
2.1.1 時間に変動がないとき
最も単純な例から始める。表1を参照。表中のケース1では、工程A~Eの処理時間(Tp)はすべて10分。投入間隔(Ti)も10分。バラツキはない。ある時刻に工程Aにワークが投入される。10分後に処理が終了しワークは移動し工程Bの処理が始まる。説明を簡単にするため移動時間はゼロとする。工程Aの処理が終了すると同時に投入された次のワークの処理が始まる。これを繰り返し、工程Eの終了で完成。この流れの中で、Tiと工程AのTpが同じで、それ以降の工程終了時刻と次工程の開始時刻が同じなので、すべての工程で待ち時間(WT)も手空き時間(FrT)もゼロとなる。生産リードタイム(LT)は各工程のTpの合計50分となる。表1参照。

表1 投入間隔(Ti)、工程処理時間(Tp)にバラツキがないとき
ケース2は工程CのTpを10分から8分に短縮した場合である。最初に①が投入される時刻を0分として、各工程の通過時刻を追ってみる。工程Bの終了時刻は20分、工程Cへの到着時刻も20分。工程Cでは8分で処理が終わるので終了時刻は28分。工程Dへの到着時刻は28分、処理は10分かかるので、工程Dの終了時刻は38分。工程Eへの到着時刻は38分で終了が48分。
工程Cでは28分に処理を終了するが、工程Bから流れてくるのが30分なので、2分間の手空きが生ずる。完成までのTpの合計は48分、LTは、工程Cで2分間の手空きが生じるがその影響はなく48分。LTはワークが生産ラインを流れる時間である。手空きにより待つのは工程(作業者)であり、ワークが待つわけではない。従って工程で生じる手空きはLTには関係しない。手空きにより工程Cの稼働率は100%から80%に下がることに留意。図2参照。
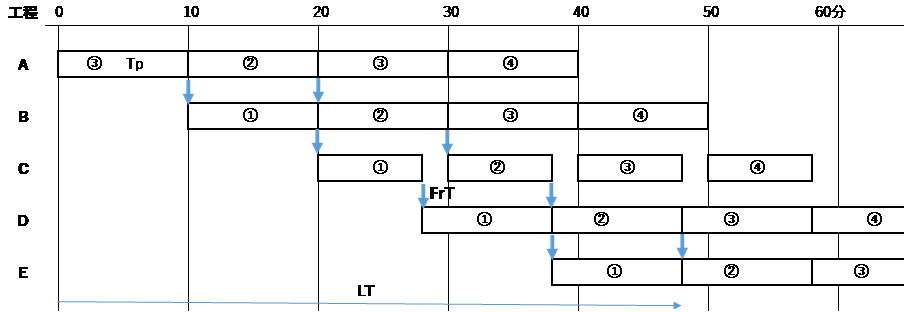
図2 ケース2;工程CのTpが短縮するとLTが短縮し、FrTが生じる
ケース3は工程B、C、DのTpが各々8分に短縮した場合である。工程B、C、Dでそれぞれ2分の手空きが生じる。Tpの合計は6分短縮されたので44分。LTも44分となる。工程B、C、Dの稼働率がそれぞれ、100%から80%に下がる。図3参照。
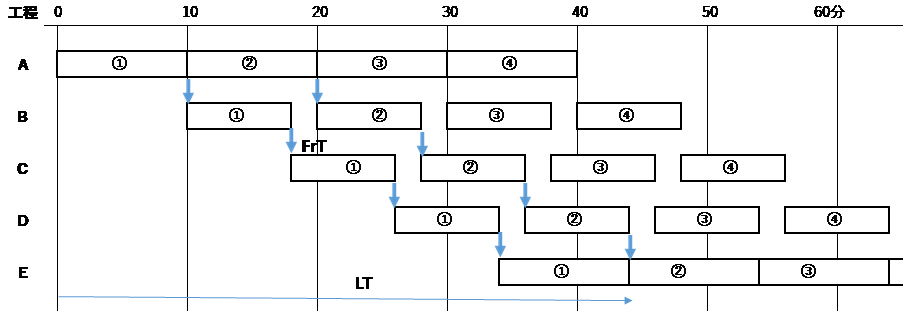
図3 ケース3 工程B、C、DのTpが各々8分に短縮
次に、工程Cが10分から12分に長くなった場合を考えてみる。表2を参照。工程Aの終了と工程Bへの投入が時刻10分。工程Bの終了と工程Cへの投入時刻が20分。工程CのTpは12分なので、工程Cの終了時刻は32分。工程Dの投入時刻も32分、終了が42分。工程Eの投入時刻は42分、終了が52分。

表2 工程CのTpが12分の場合
10分後に②が投入される。工程A、工程Bでは待つことなく処理されるが、工程Bが終了したとき工程Cではまだ①を処理中なので、ワークは待たなければならない。②が工程Bを終了し工程Cに到着する時刻が30分、工程Cで①の処理が終了する時刻が32分なので、2分間待つことになる。
③が工程Bを終了する時刻は40分。その時、工程Cでは②を処理中で終了するのが44分なので③は4分待たなければならない。同様に、④は6分、⑤は8分待つことになる。
①が工程Dで処理が始まる時刻は32分、終了が42分。②が工程Cから流れてくるのが44分なので、工程Dは2分間手空き状態となる。工程Dでの②の処理開始時刻は44分、終了が54分。工程Eも②以降、同様に手空きが生じ、②の開始時刻が54分、終了が64分となる。
LTは、①は工程Cの前で2分の待ち時間があるので、(Tpの合計50分+WTが2分)で52分。②のLTはWTが2分長くなり4分となるので54分となる。③のLTは56分、④のLTは58分、⑤のLTは60分となる。各工程の稼働率は工程A、B、Cは100%だが、工程D、Eは83%となる。図4を参照。
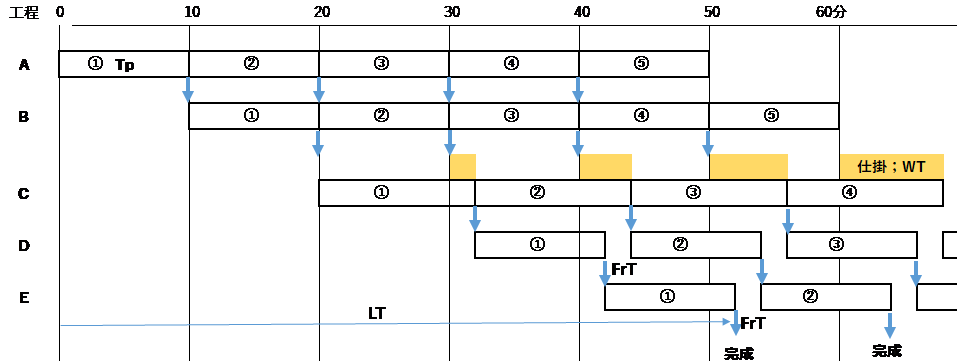
図4 表2で各ワークの工程の流れを示すガントチャート
では、工程Bと工程Dの2つの工程で処理時間が12分となった場合どうなるか。Tpは4分長くなりTp合計は54分、WTは投入毎に累積され増えていき、LTは表3のようになり、そのガントチャートは図5のようになる。稼働率は、工程A、B、Dが100%、工程C、Eが83%となる。

表3 工程Bと工程DのTpが12分の場合
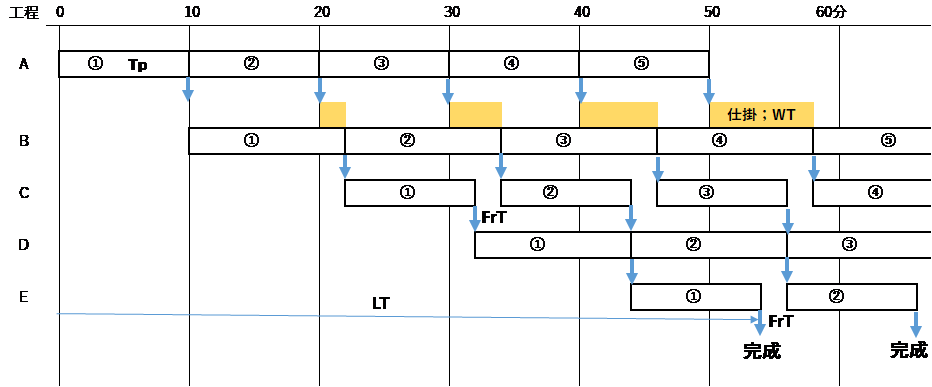
図5 表3で各ワークの工程の流れを示すガントチャート
2.1.2 生産ラインの特性をザックリとみると
生産ラインの特性をザックリとまとめてみると、表1は、投入間隔(Ti)≧最長処理時間(最大Tp)の条件である。その時、待ち時間(WT)の発生はないが、FrT=Ti-Tpの手空き時間が発生する。投入から完成までのリードタイム(LT)は、各工程のTpの合計となる。FrTはLTに加算されない。
表2と表3の条件は、Ti<最長Tpである。この条件下では、前工程からの到着Tiが自工程のTpより短いため、自工程の前でワークは待たなければならない。つまりWTが発生する。その状態が続けば、時間(t)経過とともに投入数が増えてWTは長くなる。LTは各工程のTpとWTを合算した時間である。LTにFrTは加算されない。まとめると表4のようになる。
| WT | FrT | LT | |
| Ti>Tp | 0 | Ti-Tp | ΣTp |
| Ti=Tp | 0 | 0 | ΣTp |
| Ti<Tp | 投入ごと長くなる | 0 | ΣWT(t)+ΣTp |
表4 Ti、TpとWT、FrT、LTの関係
2.2 時間に変動があるとき
日本の製造企業の99%以上が中小企業で、その大部分は多品種・少量・変量受注生産だと言われている。このような生産環境では到着間隔(Ti)や各工程の処理時間(Tp)は独立に、且つランダムにバラツく。特にWTは過去の状態の影響を受けるために、解析が難しい。
2.2.1 ひとつの工程で考えてみる
先ずは、基本的なメカニズムを知るために、ひとつの工程に注目して、用いる記号を再確認しておく。
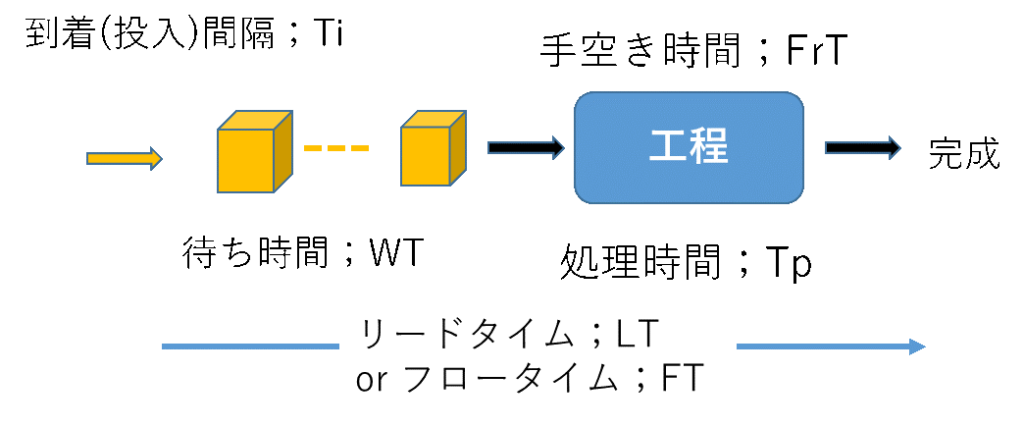
図6 ひとつの工程、用いる記号
それぞれの平均、変動係数および稼働率を以下の記号で表す。
WT;ワークの待ち時間およびその平均
注)WTの変動係数はなし(数理モデルで扱えないため)
Ti;ワークの到着間隔(投入間隔)およびその平均
Sti;Tiの変動係数 (変動係数=標準偏差÷平均値)
Tp;工程処理時間およびその平均
Stp;Tpの変動係数
ρ;稼働率 ρ=Tp÷Ti
FrT;手空き(手待ち)時間およびその平均
LT;生産リードタイムおよびその平均
(LTと同じ意味でFT;フロータイム も併用する)
一般的には、求めたい時間はWTやFrT、LTである。TiやTpがバラツクので、これらの時間も当然バラツク。きちんと理解するためには、その平均とバラツキの程度を示す分散(偏差)を知る必要がある。しかし、WTやFrT、LTの分散を求める数理モデルは、TiやTpの分布を指定しなければならない等、限定的条件付きであり、一般的で実用的なモデルは見つかっていない。
ここでは平均値と分散がわかれば使える近似式を使う。近似式だが、WTやFrT、LTの特性を知ることはできる。待ち時間の平均;WTの近似式は次のようになる。
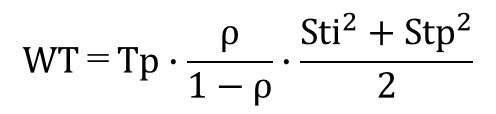
バラツキの大きさや分布形状はシミュレーションで確認することにする。シミュレーターは「SIMUL8」を使う。ただ、今回は簡易的にエクセルでシミュレーションする。エクセルの結果はシミュレーター「SIMUL8」とほぼ一致することは確認済み。
シミュレーションは以下の条件で行ってみる。
Tp=10、Stp=0.15(ガンマ分布を使用)
Ti=16.7、14.3、12.5、11.1、10.5、10.1 (ρ=0.6、0.7、0.8、0.9、0.95、0.99)Sti=1(指数分布を使用)
(時間の単位は付けていないが、分でも時間でもなんでもかまわない)
シミュレーション結果をみてみる。図7は稼働率が0.6のときのTp、WT、FT(Flow Time; LTと同じ)の分布である。Tpの分布にWTの分布が加わりFTの分布になっていることが分布形状から推察できる。
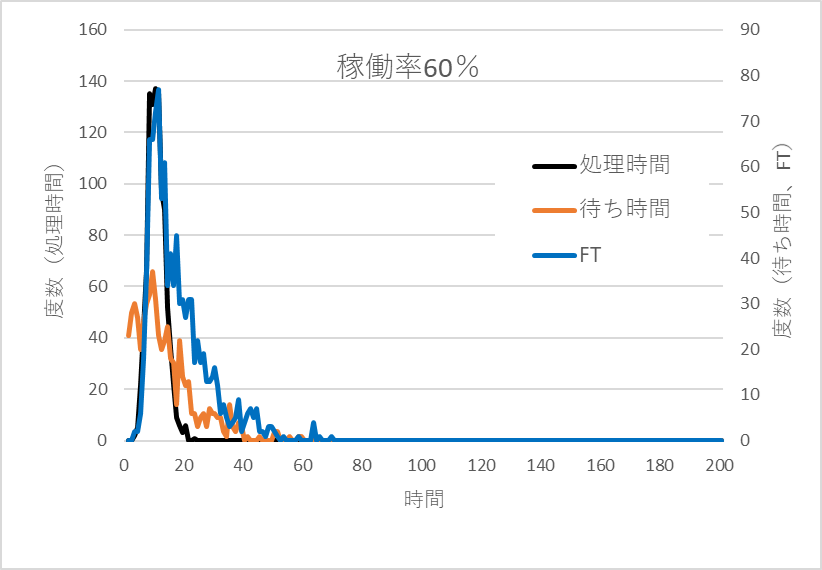
図7 稼働率60%での処理時間(Tp)、待ち時間(WT)、フロータイム(FT)の分布
図8は稼働率が0.8のときのTp、WT、FTの分布である。Tpの分布は稼働率が変わっても変化しないが、WTとFTの分布が右方向に広がっているのがわかる。
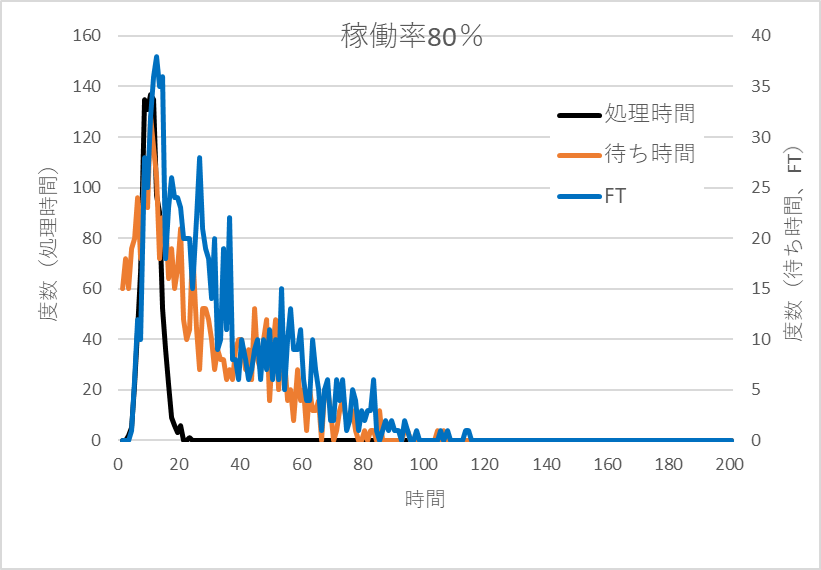
図8 稼働率が80%のときのTp、WT、FTの分布
図9は稼働率が90%のときのTp、WT、FTの分布である。WTおよびFTの分布はさらに右方向に広がり200を超えている。
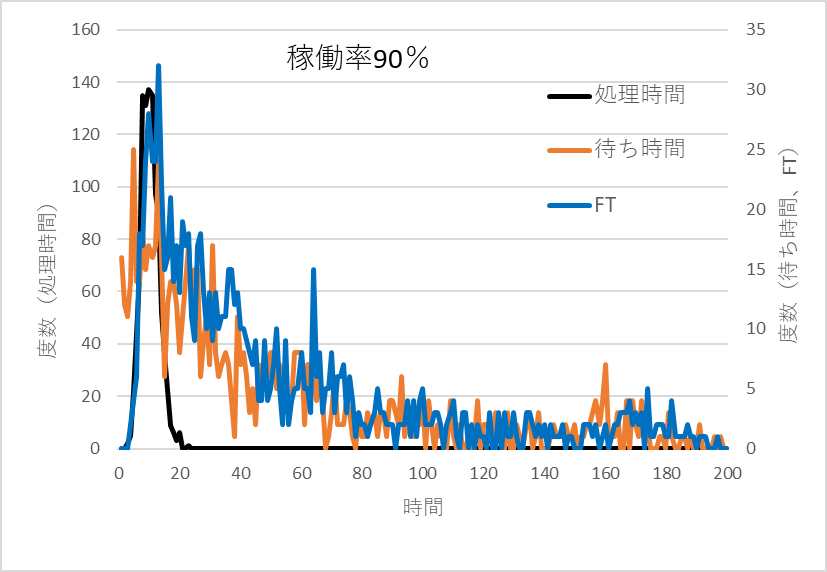
図9 稼働率が90%のときの Tp、WT、FTの分布
図10は稼働率が0.5~0.99のときのWTの分布を重ねて示している。稼働率が高くなるに従いWTが長くなる様子がわかる。Tpが10に対してWTが500だとWTはTpの50倍ということになる。
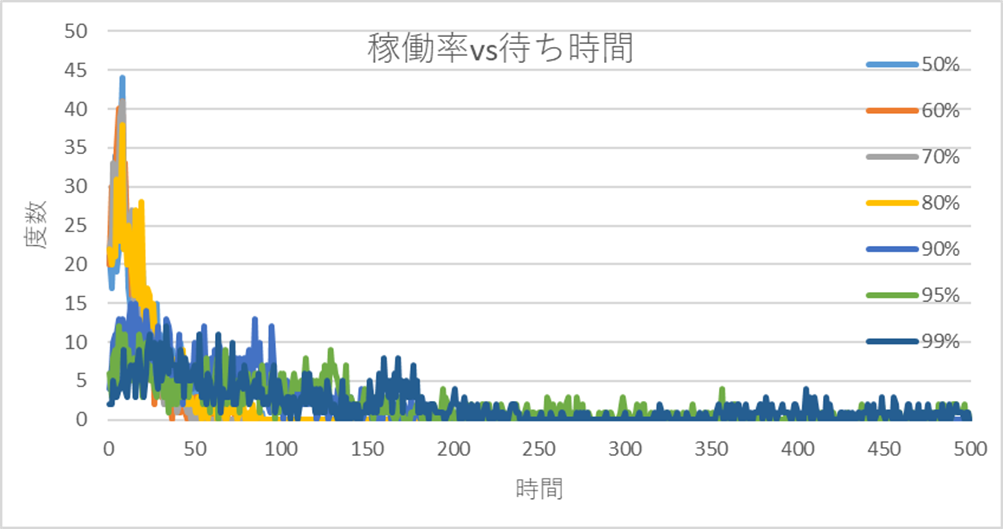
図10 稼働率に対する待ち時間(WT)の分布
図11は稼働率に対するWTの変化を示している。ひとつは、先に示したWT平均を求める近似式で計算したもの、二つめは、シミュレーション結果の平均、三つめは得られたデータの最大値である。稼働率が高いところでシミュレーションのデータが小さい値になっているのは、シミュレーション時間が十分に長くないことが原因だと考えられる。
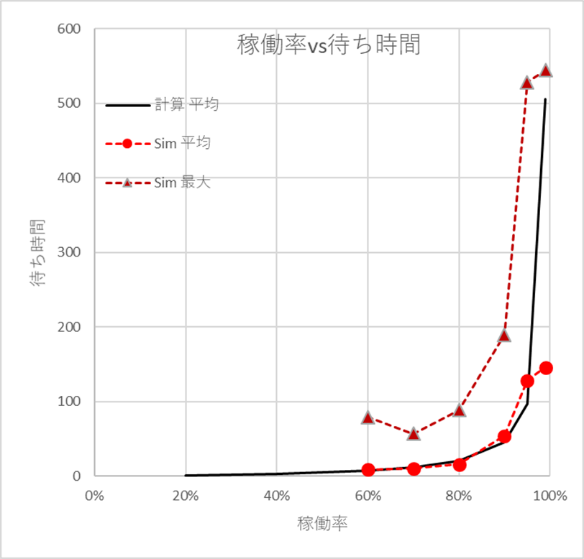
図11 稼働率v.s.WT
2.2.2 複数の工程がある場合はどうなるか
図12に示す5工程から成る生産ラインを例に、生産リードタイム(LT);[フロータイム(FT)と同じ]がどうなるか、シミュレーションで確認してみる。Tpは工程Bと工程Dが平均12分、他は平均10分で、全工程 変動係数0.5のガンマ分布とする。Tiは指数分布で、稼働率を60%、80%、90%の3種類とするため、それぞれTiの平均は①稼働率60%では20分、80では15分、90%では13.3分と設定する。(生産ラインのボトルネック工程の能力を基準として設定)

図12 5工程生産ライン;TiおよびTpが変動する場合
図13にシミュレーション結果の1例を示す。図の最上段は各工程終了時の累積処理時間(Tp)の分布である。工程を経るごとに加算されていくのがわかる。バラツキは分散の加法性が成り立つ。稼働率が変わってもTpの分布は影響を受けない。
上から2番目は工程を経るごとの待ち時間(WT)の分布である。WTは工程を経るごとに左方にダラダラと尾を引くような形状であることが特徴である。但し、これを定量的に記述する実用的な数理モデルはない。
上から3番目はフロータイム(FT)の分布である。FTは各工程のTpとWTが累積された時間である。分布形状は山形ではあるがピークに対して非対称で、TpとWTが合算されたことが読み取れる。
最下段は生産ラインの投入から完了までのTpとWTおよびFTの分布形状である。
図14は稼働率が90%のときのTp、WT、FTの分布を示す。Tpの分布は稼働率の影響は受けないが、WTの分布はだだっ広く広がり、どこにピークがあるかもわかりづらい。WTのバラツキ(分散、標準偏差、)を定量的に求めることができないうえに、分布形状が非常に広く確率計算も難しいことが推察できる。
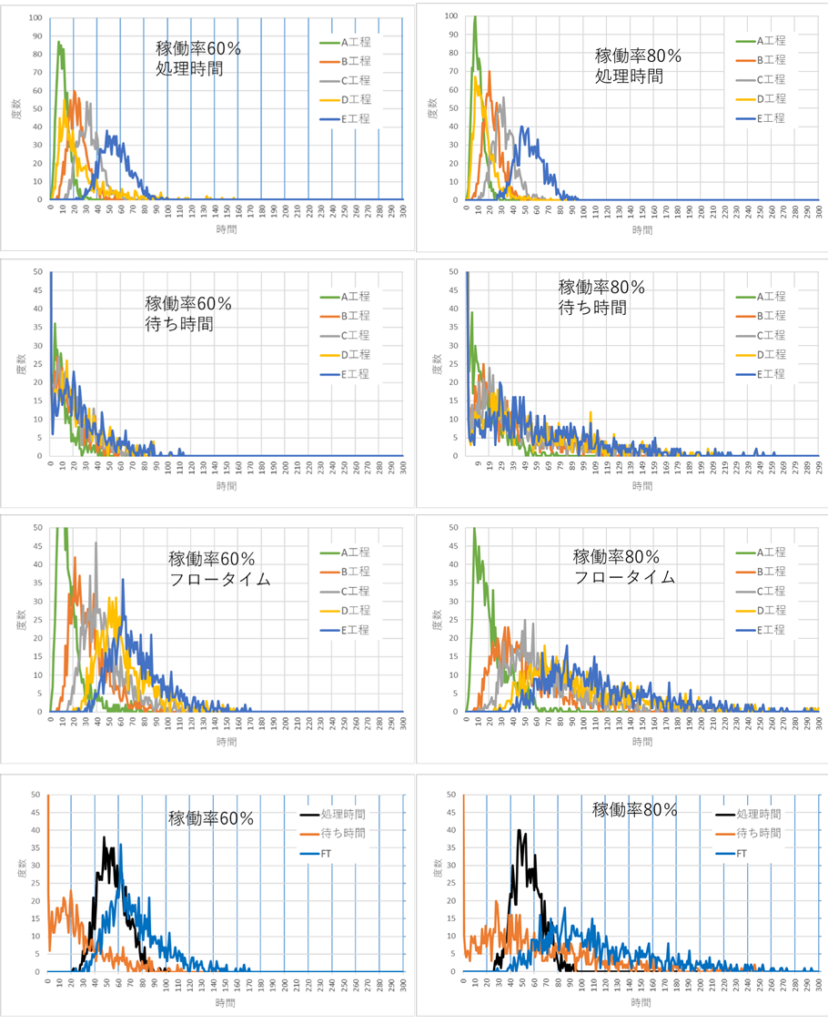
図13 稼働率60%と80%の各工程終了後の処理時間(Tp)、待ち時間(WT)、フロータイム(FT)および投入から完成までのTp、WT、FTの分布
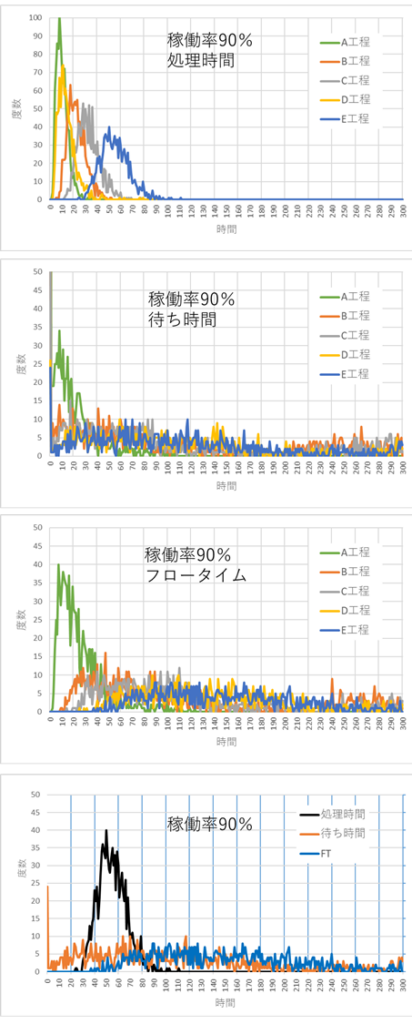
図14 稼働率90%の各工程終了後の処理時間(Tp)、待ち時間(WT)、フロータイム(FT)および投入から完成までのTp、WT、FTの分布
2.3 手空き時間(FrT)はどうなるか
手空き時間(手待ち時間)は代表的なムダと言われ、現場改善のターゲットとなっている。FrTがどのような特性、特徴があるのか、みておく。基本的な特性をみるために工程がひとつ、Tiの分布は指数分布、Tpの分布は変動係数0.5のガンマ分布を使う。結果の1例を図15に示す。稼働率が低いときはFrTが長く、稼働率が高くなるに従いWTが長くなる様子がわかる。
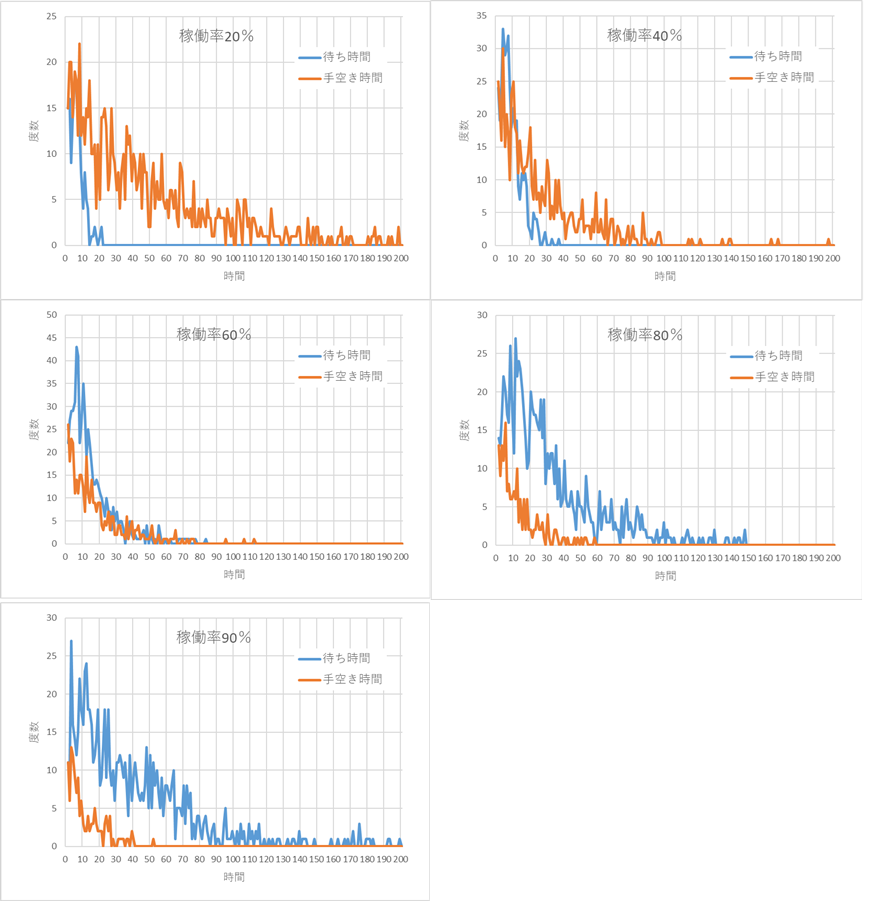
図15 待ち時間(WT)と手空き時間(FrT)、稼働率 20%、40%、60%、80%、90%
図16は、5工程生産ラインにTiは12.5分、一定、各工程のTpはすべて同じで平均10分(稼働率80%)、Stp(変動係数)は0.5のガンマ分布としたときの、FT、WT、FrTの分布状態である。
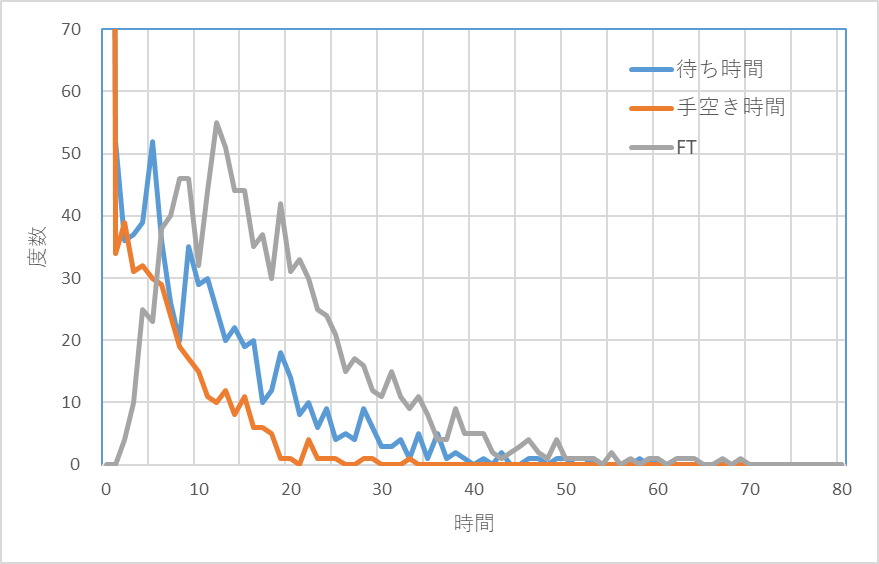
図16 5工程生産ライン、Ti;12.5分一定、Tp;平均10分、Stp;0.5のガンマ分布
WTとFrTは分布形状が似ている。稼働率が高くなるとWTが長くなりFrTが短くなるが、稼働率が低くなるとWTは短くなりFrTは長くなる。この関係を見やすくするために、それぞれの平均をみてみる。Ti、Tp、FrTの間には次の関係がある。
Ti=FrT+Tp
ρ=Tp/Tiで変換し、整理するとFrTは次のように表される。
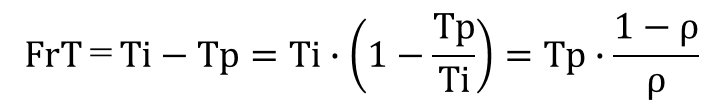
Ti、Tpの変動係数Sti、Stpを考慮したFrTは、WTの近似式を援用して、次のように記述できる。
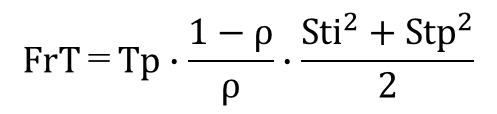
ここで、WTとFrTの関係を見やすくするために、Tp=1、Sti=1、Stp=1とすると、
FrT=(1-ρ)/ρ
WT=ρ/(1-ρ)
となる。図17にρに対するWTとFrTの特性カーブを示す。点は、シミュレーションで求めた結果である。
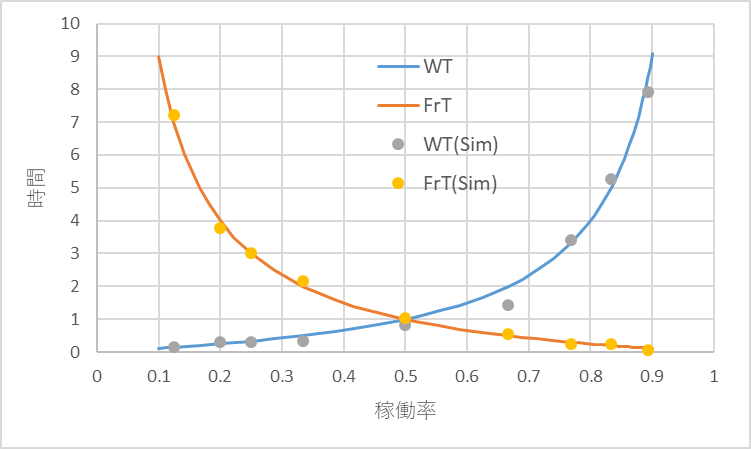
図17 稼働率(ρ)に対するWTとFrT
FrTの特性を概観してみた。主な特徴は以下のようである。
- 稼働率に対して、ほぼ反対の特性である。
- FrTの近似式は次のようになると考えられる。
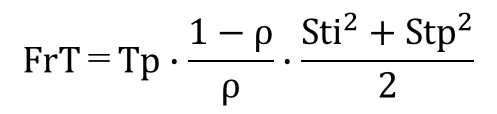
- 近似式(曲線)とシミュレーション(点)はよく一致する。
- FrT、WTの分散を求める式はないが、両者の分布形状は酷似している。
2.4 まとめ
*n工程直列ラインの平均生産リードタイム(LT)は、各工程の平均WTの合計と各工程の平均Tpの合計を加えた時間となる。
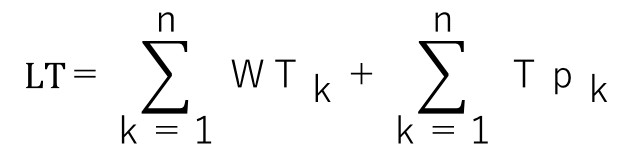
*生産ラインの総処理時間は工程ごとの平均Tp(Tp1、Tp2・・・Tpn)の合計である。
*WTとFrTの平均を求める近似式は次の通り。
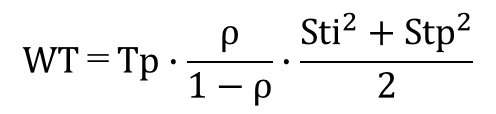
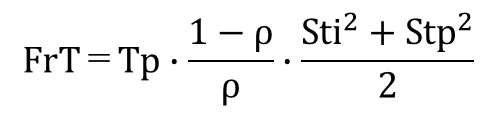
*WTおよびFrTの分散を求める数理モデルはないが、シミュレーションにより分布形状や分散を求めることはできる。
*WTおよびFrTの分布形状は右肩下がりでだだっ広い。統計理論を援用しても実用的な確率で解を求めることは困難。WTやFrTのバラツキを抑制する策を併用し、その抑制程度に合った管理方法を模索することになる。
3、トヨタ生産方式と設計情報転写論に依拠した「2種時間概念」
「2種時間概念」の「作業時間」と「生産リードタイム」の2つの時間について論じる時、必要な時間要素は、
- 生産ラインへの投入間隔と工程への到着間隔;Ti とそのバラツキ(変動係数)Sti
- 工程での処理時間(加工、組立、);TpとそのバラツキStp
この二つの要素から、
- 工程前でワークが待つ時間;WT
- 工程がワークの到着を待つ時間;FrT
が決まる。つまり、Ti、Tp、WT、FrTの4つの要素で生産ラインの時間特性を記述することができる。
ところが、「2種時間概念」を繰返し読み返しても、上記のような生産ラインの時間特性に関する言及はない。関連するそれらしき説明として、次の記述はあるのだが、、。
「現場改善会計を体系的に展開するため、改めて基本原理を確認する。」
GKCの体系化で、基本原理として依拠した理論は「トヨタ生産方式」と「設計情報転写論」(藤本隆宏)である。「トヨタ生産方式」(以下、TPS)の特徴は、Just In Time。工程で作業が開始する時刻に間に合うようにワークが到着し、作業が終わると同時に次工程の作業が始まる。これを上記の記号を使って記述すれば、
WT=0、FrT=0
であり、それを実現する条件は、
Ti=Tp、Sti=0、Stp=0
である。つまり、稼働率100%、生産リードタイム=Σ各工程処理時間である。
具体的には、平準化、標準時間の維持管理、ムダ取りなどの改善、混乱の拡大を防ぐ自働化などなど。一朝一夕に出来上がったものではなく、原型ができあがるまでには20年近くの年月を要している。TPSが世に知られるようになって40~50年たつが、TPSを再現できた企業はごくわずか。多くの企業は失敗している。つまり、TPSは生産システムのお手本とはなっても、世の一般企業を対象として、改善効果の金額評価方法確立のために依拠する普遍的な生産方式にはなりえないのである。
さらに、「設計情報転写論」に依拠したことは愚行を決定づけるダメ押しとなっている。提唱者の藤本隆宏元東大教授著「生産システムの進化論」(1997)はトヨタに焦点を当てた企業進化論である。そのなかで、生産リードタイムを次の式で説明する。
生産リードタイム=1/(情報受信スピード×情報受信密度)
この式をどのように使って、生産ラインのリードタイムを解析し、その短縮の改善策に結び付けるのか、工学的、物理的な説明はない。生産ラインの特性を理解できていない証左である。
彼の“進化論”の結論めいたものは、「トヨタの進化は怪我の功名」だ、と。この「迷論」は歴史に残しておく価値がありそうだ。
「現場改善会計論」の裏側に広がる“闇”は思ってた以上に広く、深い。もう少し、“暗黒”の中をさまよってみるか、、、