藤本隆宏教授が主張する設計情報転写論。開発は設計情報の創造 、 調達は媒体確保 、 生産は媒体への転写 、 販売は構造設計情報の発信 、 サービスは機能設計情報の発信であると説きます。そのような付加価値を担う設計情報の流れを一貫して分析し、「広義のものづくり経営学」として体系化しようとしているようです。
ところが、設計情報転写論は生産現場では使えないことがわかりました。サービス業、具体的には医療現場にも適用できるという藤本教授の動画をみましたが・・・やっぱりダメ、使えません。
1、建築現場なら使えるかも・・・
で、Webをググっていたら、こんなファイルが見つかりました。
ものづくり産業論からみた建築 これは、建築研究開発コンソーシアム の創立20周年記念講演会(2023年2月8日)で藤本教授が講演したとき使ったもののようです。
建築現場なら使えるかも・・・。というよりは、建築現場で使えないのなら、設計情報転写論を適用できる分野はあるの? となってしまいます。そう思った理由について簡単に触れておきます。
先ず、生産現場も建築現場も“モノ”(材料、部品、加工対象物、製品、家、ビルディング、、)があり、その“モノ”をつくる“リソース”(人、機械、設備、、)があります。
生産現場はリソースが工場内にほぼ固定されていて、そこをモノが流れ、完成品となります。共通のリソースを使ってたくさんのモノをつくる工場の基本形ですね。
一方、建築現場では決められた場所に、材料を運び込み、リソースが入れ代わり立ち代わり入りモノをつくります。
生産現場はリソース基準でモノが流動。建築現場はモノが基準でリソースが流動。
もちろん、実際は、きれいに分けられない部分もありますが、ザックリとみればモノとリソースの関係はこんなふうにみることができるのではないかと思います。
2、事例で考える
次のような一戸建て住宅の建築を例に、もう少し掘り下げて考えてみたいと思います。
着工(地盤調査~水道工事);3週間
基礎工事(配筋検査~木造積上) ;4週間
棟上(屋根工事~外装);3週間
仕上(内装~外構);3週間
完成・引渡(竣工検査~引渡);2週間
着工~完成まで15週間で1軒が完成する計画です。これと比較しやすいような、第1工程~第5工程から成る生産ラインの例を図1に示します。工程の処理時間の数値は同じですが単位は分とします。投入から完成までの生産リードタイムは15分となります。ボトルネックは第2工程で処理時間が4分ですので、4分間隔で材料が投入されれば、1日当りの生産個数は480(分)÷4(分)=120(個/日)となります(立ち上がり期間は除く)。
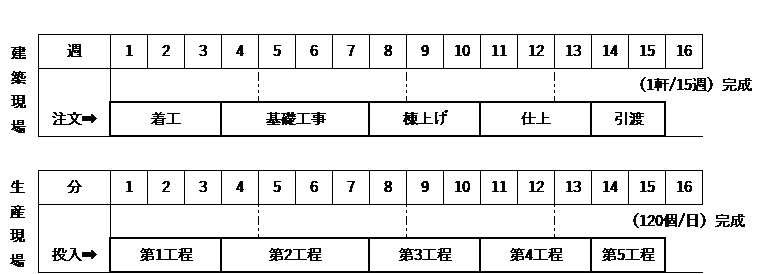
図1 建築現場と生産現場のスケジュール例
この計画にいろいろな条件を設定して、シミュレーションや数式を使ってその結果がどうなるかをみてみます。
2.1 バラツキがある場合
では、工事期間や工程処理時間がバラツク場合はどうなるでしょうか? 各工事、工程のバラツキを一律に変動係数(標準偏差/平均)0.3でバラツクとします。シミュレーション結果を図2に示します。着工~完成・引渡は平均で15週間、最短10週間~最長22週間ぐらいにバラツクようです
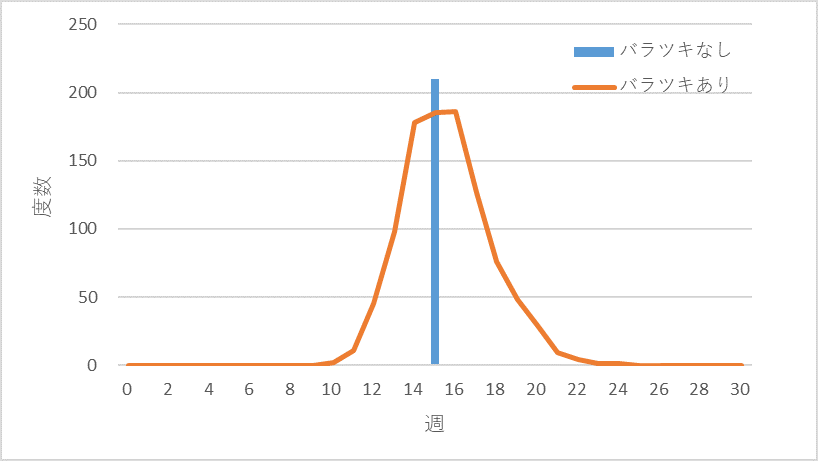
図2 着工~引渡の期間、バラツキがない場合とある場合
2.2 計算式で求める
計算式で求めることもできます。着工から完成までの工期の平均と分散は加法性があるので、その性質を利用して次のように計算できます。
平均工期=着工平均+基礎工事平均+棟上げ平均+仕上平均+引渡平均
分散=着工の分散+基礎工事の分散+棟上げの分散+仕上の分散+引渡の分散
数値を入れて計算すると、
平均工期=3+4+3+3+2=15
分散=(3+4+3+3+2)*0.3=4.5
シミュレーション結果と計算で得られた平均15、分散4.5の分布(ここではガンマ分布を使います)を重ねると図3のようになり、計算値とシミュレーション値がほぼ一致することが判ります。
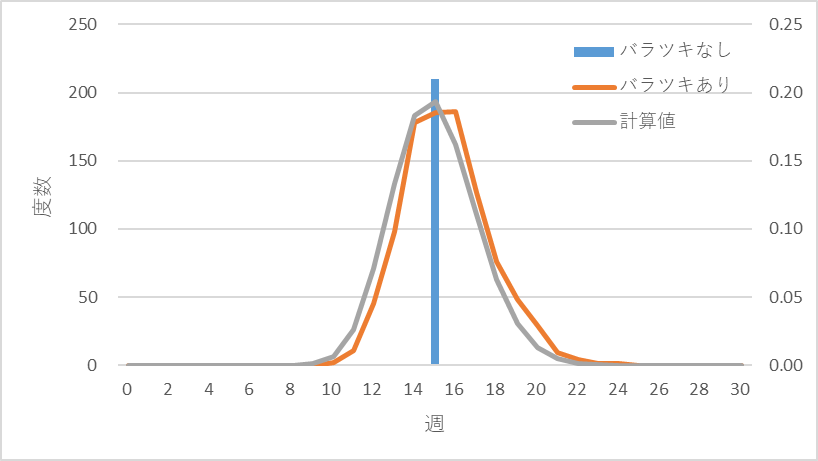
図3 シミュレーションと計算結果
2.3 生産ラインではどうなるか
生産ラインではどうなるかをみてみます。建築現場では一軒一軒個別で管理しますが、生産ラインでは連続して材料を投入し、ある時間、例えば1日8時間とか、連続して稼働します。このような稼働状態のとき、生産ラインの能力に対してどの程度の負荷をかけるかが重要なポイントになります。生産能力に対する投入負荷の割合(負荷率や稼働率)を75%、85%、95%としたとき、処理時間、待ち時間、リードタイムのシミュレーション結果を図4~図6に示します。
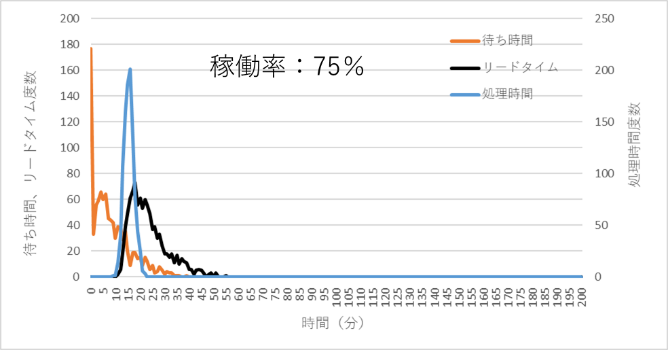
図4 稼働率75%での処理時間、待ち時間、リードタイムの分布
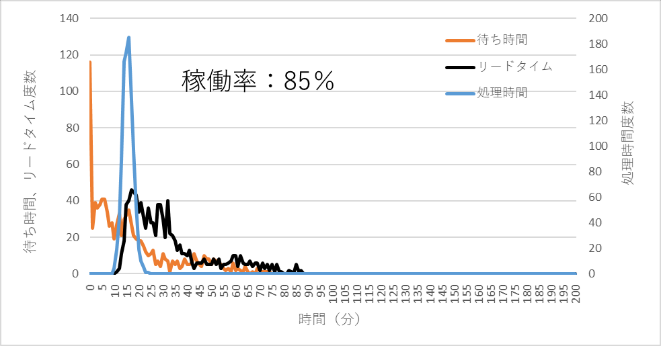
図5 稼働率85%での処理時間、待ち時間、リードタイムの分布
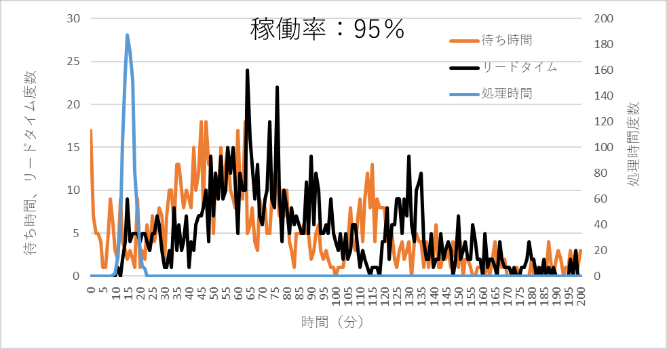
図6 稼働率95%での処理時間、待ち時間、リードタイムの分布
同様の図は前にも紹介しておりますので、詳細な説明は省きますが、稼働率が高くなるとリードタイムがダラダラと長くなるのがわかります。リードタイムは各工程の処理時間と各工程の前でワークが待つ時間の合計ですが、待ち時間の影響が大きいことは一目瞭然です。
2.4 生産現場;見込生産を想定
前の条件は、注文がランダムに飛び込んでくる受注生産をイメージして投入間隔は指数分布を使いましたが、見込生産の場合は一定間隔で投入することができます。投入間隔はボトルネックの能力に合わせて4分(稼働率100%)一定としてシミュレーションした結果を図7に示します。4分一定間隔で投入する方が分布の広がりも狭くなり、リードタイムは短くなります。
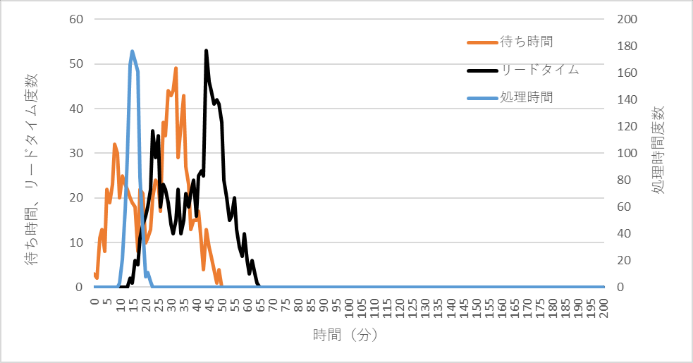
図7 4分一定間隔で投入(見込生産を想定)
2.5 建築現場;前の工事が早く終わっても次の工事は予定通り始める
建築現場では前の工事が早く終わっても、工事ごとに予定が決められていて、予定にしたがって工事を始めるケースが多いと思われます。また、予定に対して実際の工期の平均は短いのが普通です。平均値を1σ分だけ短かくして(表1参照)、予定より早く終わっても次の工事はあらかじめ立てた予定通り始めて、予定より遅れた場合は前工事が終了後直ちに始めるという条件でシミュレーションしてみます。
| 工事 | 予定期間(週) | 平均(週) | 変動係数 |
| 着工 | 3 | 2.1 | 0.3 |
| 基礎工事 | 4 | 2.8 | 0.3 |
| 上棟 | 3 | 2.1 | 0.3 |
| 仕上げ | 3 | 2.1 | 0.3 |
| 完成・引渡 | 2 | 1.4 | 0.3 |
表1 実際の工期を想定した設定例
シミュレーション結果は図8のようになります。実際の工事期間は短くなりますが、工事と工事の間が休みとなり、前の工事が遅れた影響で後ろにズレますが、図3と比べると工事期間のバラツキは小さくなります。実際は、こちらに近いのではないでしょうか。
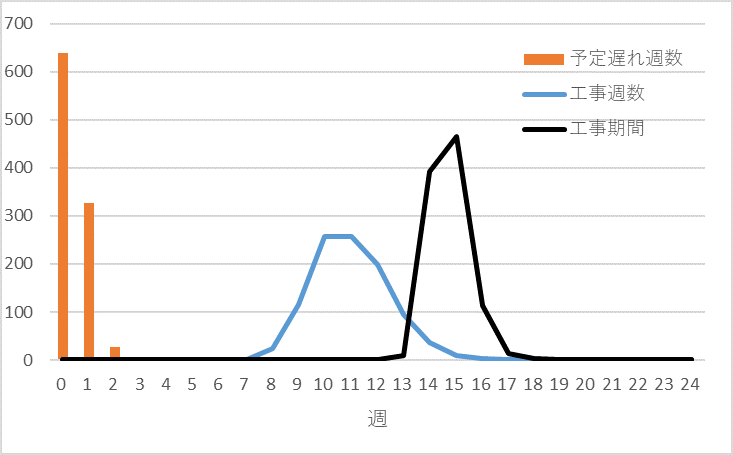
図8 予定より早く終わっても予定通り始める場合
図8の水色が前の工事が終わったら直ちに次の工事を始める場合の工事期間(リードタイム)の分布、橙色が予定以内(横軸;0)と予定より遅れる(横軸;1以上)確率の分布、黒色がリードタイムの分布です。
3、建築現場と生産現場の違いは、なぜ生じるか?
建築現場の仕事の流れと生産現場のそれとを比べてみました。大きな違いがあることが判ります。“モノづくり”という視点からみれば、どちらも材料・部品があり、作業員が機械・道具を使ってつくる。同じようにみえます。しかし、「流れ」という視点から、流れの良し悪しの目安となるリードタイムをみれば、より正確には正味処理時間合計に対するトータル・リードタイムの長さをみれば、明らかな違いがあります。なぜ、このような違いが出るのか考えてみたいと思います。
3.1 リソースとモノ(家屋、製品、)の相対的位置関係
図1をみれば、建築も生産も同じようなチャートで仕事の流れを表すことができますが、リソース(作業員、機械、道具、、)とモノ(家屋、製品、、)の相対的位置関係に違いがみられます。冒頭、言及したことですが、重要なことなので、再度確認しておきます。
建築現場では、リソースが入れ替わり立ち代わり入り、家屋がつくられる。一方、生産現場では、設置された多工程から成る生産ライン(リソース)の中を被加工物が流動し、製品がつくられる。
つまり、
建築現場では、家屋(つくるモノ)が固定されていて、リソースが流動するが、生産現場では、リソースが固定されていて、製品(つくるモノ)が流動する、と解釈できます。
3.2 リソースの流動性、管理時間粒度の違い
例えば生産現場で、工程前の仕掛が急に増えだしたとき、どのような手を打つでしょうか? 調べてみたら注文が増えて、しかも工数の喰う品種が多いことが判ったとします。リソースの追加をしたいところですが、必要な技能のある作業員を追加するのはたやすいことではありません。機械設備を追加するとなったら月単位の時間がかかります。残業等でカバーするとか、ある程度の挽回策は打てますが、残業が恒常化してれば効果も限定的。営業と丁々発止の優先順調整で現場の混乱は常態化してしまいます。
一方、建築現場。例えば、工事中に機械が故障して、修理に1~2週間かかりそうだとなったとき、ハウス・メーカーや工務店によって対応はさまざまだろうと思いますが、代替の機械なり、対応可能な業者なりを手配して遅れを最小限に抑えるというようなことはよくあることではないかと思います。工場内にほぼ限定された生産現場よりも、リソースの調整範囲が広いといえるのではないでしょうか。
また、管理時間粒度も、生産現場は“分”、建築現場は“時間~日”という違いも影響するかもしれません。
3.3 建築現場のリードタイムは計算できるが、生産現場のリードタイムは計算できない
建築現場でも工事業者ごとにみれば、忙しい工事業者もあれば比較的余裕のある業者もあります。忙しい業者は掛け持ちで工事を行っていて工事期間のバラツキも大きいとか、中には経験の少ない業者がいて工事期間が不安定だということもあるでしょう。ただ、このような場合でも、先々の予定を計画することはできます。なぜかと言えば、各工事期間の平均と分散をそれぞれ合計することで全体のリードタイムの平均と分散が求められるという加法性があるからです。
しかし、生産現場での投入から完成までのリードタイムは計算では簡単に求められません。各工程の平均と分散を加算して求めることができるのは正味処理時間の合計、つまり、完成品1個の正味処理時間だけです。リードタイムを求めるためには、各工程で待つ時間を加える必要があります。ところがこの待ち時間、平均を求める近似式はありますが、バラツキを求める数式はありません。平均を求める式も、定常状態という生産現場ではありえない状態を条件としていますので、参考程度にしか使えません。
シミュレーションで求めることはできますが、シミュレーションごとに結果がかなり異なり、また、だだっ広い分布となるために実用的な推定値を求めることも困難となります。
このようなことが、建築現場と生産現場の違いが生じる要因と考えられます。
4、設計情報転写論はまったく、使いものにならない
生産現場や医療現場では待ち行列による待ち時間が発生しますが、設計情報転写論では待ち行列現象をまったく考慮していません。それが、設計情報転写論が生産現場や医療現場で使えない理由です。
建築現場では待ち行列現象の発生はあっても、実用上は無視できる程度です。であれば、待ち行列現象を考慮しない設計情報転写論は建築現場では使えるのではないか、と思われるわけです。
で、ものづくり産業論からみた建築 に「良い流れ」度の基本公式っていうのがあります。設計情報転写論の裏付けとなる数理モデルのようです。

図9 設計情報転写論;「良い流れ」度の基本公式(ものづくり産業論からみた建築より引用)
リードタイムに関する公式を再掲します。
1/リードタイム=設計情報受信の速度×受信密度
で、この式、どうみても理解できません。シミュレーション結果からわかるように、上式が生産ラインのリードタイムを記述していないことは明らかだし、建築現場のリードタイムを記述しているわけでもないし、いったいこの公式って、何なんでしょうね?
建築現場の流れでは、待ち行列現象は無視できる程度なので、設計情報転写論は使えるのではないか、という期待はありました。
しかし、設計情報転写論は重要な基本特性を捨象しているだけではなく、「流れ」の基本的なメカニズムも正しく取り込めていません。「良い流れ」を実現するための拠り所である「設計情報転写論」の説明は “お粗末” 極まりなく、その論理は“デタラメ”です。
設計情報転写論は “お粗末” で “デタラメ” です。