No.66 新たな段階に入った在庫管理論の本質
受注件数Nの平均 
と分散Vn、１件当り受注数(以下、量/件)の平均
と分散Vqがわかっているとき、受注量の平均
と分散Vdは次の式で求めることができます。
-------(式１)
-----(式2)
この式、これまでの在庫管理論を一新するほどのインパクトがあることがわかってきました。実際は、この式だけでそうなるわけではありません。もうひとつ、重要な要素が加わります。と言っても、それって、珍しくもなんともない、生産管理、在庫管理に携わっているかたならだれでも知っているやつ。何かって？、、、 それは、かんばん方式。
かんばん方式と上式で、在庫管理論が一変する？ って。そう、そうなんですよ。うさん臭く感じますか？ 生産管理や在庫管理では、不可解な説明があふれていますからね。そのたぐいの、嘘だか本当だかわからない、怪しきものと受け取る方が多いのはやむをえません。でも、中には、もしかすると、と、興味を示される方もいらっしゃるのではないか、と期待もしたいところです。
いずれの方も読み進めていただければうれしいです。
かんばん方式についてはよく知られていますように、平準化やバラツキの排除という条件の下でしか成立しない、と言われています。かんばん方式の失敗事例が後を絶ちませんが、その主な原因は、平準化ができていない、バラツキが大きいというものだそうで。ですから、かんばん方式はトヨタ生産方式でしか使われない、特殊な在庫管理方法だ、というのが大方の理解ではないかと思います。バラツキの大きい一般の在庫管理には使えない、これが通説ではないでしょうか。
かんばん方式のメカニズムはいたって簡単です。仕掛けかんばんとか引き取りかんばんとか、その他にもいろいろあるようですが、詳しいことは、解説書がいっぱい出てますので、そちらをご覧ください。ここではかんばん方式の基本メカニズムに注目します。
かんばん方式の基本的メカニズムは、ものが消費され、かんばんがはずれ、はずれたかんばんが供給元へ送り返され、部品とともに戻ってくる、ということではないかと思います。つまり、前工程が使った分だけ後工程が供給する。あらかじめ設定した枚数のかんばんがぐるぐる回るだけですから、在庫、仕掛の増加もなし。これほど簡単で理にあった在庫補充の方法はありません。トヨタ生産方式が優れている理由のひとつがかんばん方式である、という解釈に抗う人もいないのではないかと思います。
必要なかんばん枚数はどのぐらいかといいますと、単純にするために収容数（かんばん１枚当たりの数）を1、バラツキなし（安全係数０）としますと、
かんばん枚数＝補充時間の間の消費量
ここで、補充時間というのは、ものが消費されてから手元に戻ってくるまでの時間です。まとめますと、かんばん方式の基本メカニズムは、次の２点です。
①消費した分を補充発注する
②必要かんばん枚数は補充時間の間の消費量分
補充時間は外れたかんばんが戻るまでの時間の他に、収容数が消費される間の待ち時間やかんばん回収作業の時間なども含みます。様々な変動がありますので、実際は安全係数を加え、かんばん枚数は次のようになります。
かんばん枚数＝｛平均消費量ｘ（補充時間＋安全係数）｝/収容数
安全係数は3%以内でないとかんばん方式はうまくいかない、なんて説明されています。3％って、どういう意味なのか定かではありませんが、ここでは変動係数（標準偏差/平均値）と解釈しておきます。
かんばん方式が優れているのは上記の①と②のメカニズムにあるわけですが、そのメカニズムが機能するためには、変動係数が3%以下であることが条件ですよ、と。かんばん方式の失敗事例の大部分はこの条件を満たしていなかった、というわけです。変動係数が3%以下なんていう条件は、普通の在庫管理の環境では、限られたところしかできないと思いますよ。かんばん方式と一般の在庫管理の間には、とてつもなく分厚く、高い壁が存在するんですね。
かんばん方式（①と②の方法）が優れた方法であることはトヨタ生産方式が証明したことです。しかし、変動係数3%以内でないとだめですよ、といっているのもトヨタ生産方式です。少し、視点を換えてみましょう。変動係数3%は、①と②を実現するための絶対条件なんですか？ と。
実は、この条件を外すことは、簡単ではありません。これまでも数々の研究がされてきて、たくさんの論文があるようです。いくつかをパラパラとみてみましたが、難解な数式が紙面を埋め尽くし、読む気力も萎えいでしまうような論文が大半。いまなお、一般の在庫管理に①と②が広く適用されていないところをみると、幾多の論文もこの壁を乗り越えてはいないのではないか、と思うわけです。
この分厚く、高い壁を超えることができるようにしたのが、（式１）と（式２）だというわけです。
かんばん方式の優れたメカニズムである①と②を使えない理由は、ひとつ。変動係数が大きい（３％を超える）から。
トヨタ生産方式の特徴の一つは、変動の排除です。ですから、生産ラインの管理でも在庫管理でも、トヨタ生産方式の理論にはバラツキ、変動が考慮されていないんですね。３％というのは、トヨタ生産方式の理論が崩れない範囲だとも解せるわけです。
で、この変動にチャレンジ。５％ならどうなのか、10%なら、、。いやいや、変動の程度で線引きするケチな考えは止めましょう。世の中の変動をありのまま受け入れてはどうか。そんな野望を抱きながら、、。
かんばん方式の変動条件を外すためには、次の項目に変動要素を組み込む必要があります。
＊かんばん枚数の変動
＊収容数の変動
＊補充時間の変動
この３要素がランダム変動したら、それは、かんばん方式とは言えませんね。ですから、一般の在庫管理では次のような言葉になります。
＊かんばん枚数 → 受注件数；N
＊収容数 → 受注１件当り受注数量 (量/件；Q)
＊補充時間 → 納入リードタイム；T+(発注間隔、定量発注時間間隔など)
ある時間での受注量（需要）はNとQで決まります。需要は変動しますので、その変動を取り込みます。Nの分散をVn、Qの分散をVqとすると、下記の（式１）と（式２）となります。
-------(式１)
-----(式2)
次に、補充時間の変動を取り込みます。補充時間の中の納入リードタイムをT、その平均を
、その分散をVt、T間の受注件数の平均をとすると、
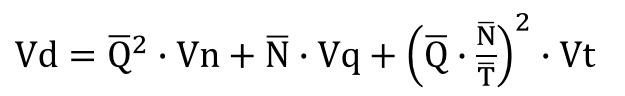-----（式3）
発注間隔、定量発注時間間隔などがどのように取り込まれるかは省略します（詳細は「在庫流動管理の基礎」や「STIC発注方式」を参照ください）。
一般の在庫管理でのかんばん枚数に相当する補充時間の間の需要は、変動がありますから、需要の最大Dmaxとなって、次の式で求めることができます。
-----（式４）
αは安全係数で、許容できる欠品率を考慮して決めます。
いかがでしょうか。かんばん方式の簡便さと在庫補充の合理性はそのまま引き継いで、平準化は困難だ、バラツキを避けることはできないというような一般の在庫管理環境でも使えるようにしたのが、（式１）～（式４）。これで、在庫管理論が新たな段階に入った、ということになります。
新在庫論とは、まとめると、こんな感じになるのではないでしょうか。
１、在庫管理論の新たな論理構成を提供する
在庫管理の主要構成要素（受注件数、量/件、納入リードタイム等）の変動を受け入れ、受注・出荷の両方向で共通の理論構成となっているため、サプライチェーンのあらゆるリンクをつなぐ共通理論となりうる。
２、在庫管理ユニット間で最適条件を見つけやすい
在庫管理ユニットの出（受注→出荷）と入り（補充発注→入庫）を共通の式で捉えることができるので、取引両者の最適な受・発注条件を求めることができる。
３、受注件数が増減する場合と１件当り注文量が増減するときの違いが判る
例えば、販売地域を広げる場合（来客数の増加）やBuy one, get one free等の販促（１人当り買上数増加）など、異なる需要増加に対する必要在庫量をより正確に見積もることができる。
４、需要に追従する見込生産の実現
自社の生産ラインから在庫補充が行われる場合、生産計画によらない需要追従型の見込生産が実現できる。工場内の部品や中間製品の仕掛管理にも適用できる。
５、不定期不定量発注（適時適量発注）の実現
最も理想的だと言われている不定期不定量発注（適時適量発注）が、定件発注で簡単に実現できる。
６、将来の需要変動に対する対策をとりやすい
対応できる需要変動範囲を明確に設定し、管理基準とすることで、将来の需要変動に対する対策が容易となる。
７、在庫の総量を把握しやすい
各SKUにそれぞれ流動インベントリーを設定するので、その総量、実在庫が常時把握できる。
８、在庫管理が簡単になる
かんばん方式の補充発注方法と同じであるため、在庫管理のオペレーションが簡単で、自動化がしやすくなる。