No.62 適正在庫を維持せよ、、というけれど

前回は流動インベントリー（STI）とその中の実在庫がどのような分布をするのかをみてみました。STIは（発注待ち＋注残＋実在庫）ですから、大きさだけみれば、流動インベントリーの大きさ（SSTI）≧実在庫　の関係があります。注目したいのは、STIに対する実在庫の位置です。

これまでの在庫管理で注目してきたのは実在庫ではないかと思います。在庫管理の目的は欠品を出さない最少の在庫をいかに維持するか、ですから具体的には、実際の在庫が倉庫に常にあるようにしながら、それをできるだけ少なくする。目前の在庫に関心が向くのは自然の流れなんでしょうね。

で、そのような在庫量を適正在庫と呼んでいるようです。定義めいた表現をすると、
「欠品の発生をある率以下にするために必要な最少の平均在庫」
とでもなるんでしょうか。平均在庫で表しているんですね。倉庫の必要面積を知るんだったら最大値の方がいいような気もしますが。

在庫関連本をペラペラめくると、「適正在庫」という言葉がやたら、目につきます。在庫は多くても少なくてもダメ。「だから適正在庫を維持しなければならない」　これに反論する人はいないでしょうね。在庫管理に携わる方々の共通認識となっているようです。

ところが、です。在庫管理の目標たる適正在庫なんですが、捉えにくいんです。実際の在庫は、入庫・出庫が繰り返されますので常に変動してます。１例を図１に示します。出荷ごとの在庫数を示しています。流動インベントリーの大きさ（SSTI）と平均（適正在庫）も示しておきます。

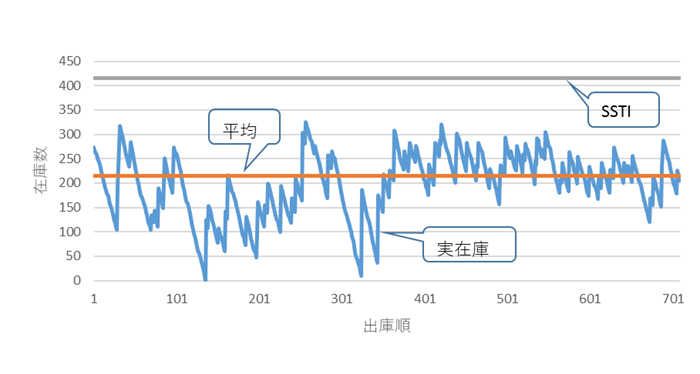
図1 実在庫の推移

適正在庫を維持しろ、ということなんですが、日常の在庫管理ではどうすればいいんでしょうね。平均値（適正在庫）を目標にするといっても、実在庫が平均値と一致するのは瞬間的というか、たまたまというか、、。実在庫が目標値（適正在庫）と合っているかどうか、よくわかりません。適正在庫を下回ったら発注量を多くして、逆の場合は少なくする、、なんてことではないし、、。入庫・出庫ごとのデータをある期間集め、平均値を計算することになるんでしょうか。やろうと思えばできないことではありませんが、、。

従来の在庫管理で代表的な定期発注と定量発注。定期発注では（納入リードタイム＋発注サイクル）間の需要量を毎回予測して、発注量を調整します。予測ですから、まぁ、おおむねはずれます。定量発注では、多くの場合、発注点を設定し、在庫がそのレベル以下になったらあらかじめ決めた量を補充発注します。調整は発注点の上げ下げで行います。このような在庫管理方法の中で、適正在庫という目標はどの程度認識されているんでしょうか。

まぁ、ありていに言えば、変動する在庫レベルをみて適正在庫かどうか判断することは至難の業。適正在庫かどうかわからないのに「適正在庫を維持しろ」とはこれいかに。在庫管理がスッキリしない一因になっているように思います。

適正在庫を維持するためにはどうすればいいかを考えてみましょう。需要の母集団は変わらないとします。

在庫管理がスッキリしない理由のひとつは、在庫から出荷され、補充発注し入庫されるまでの納入リードタイム分の時間遅れがあるからではないか、と。定量発注、定期発注、定件発注など、まとめて補充発注しますので、さらに待ち時間分の遅れも加わります。この遅れ時間も考慮しなければならないのではないか、、。

遅れ時間を考慮に入れるといっても、いちいち時間を計るのは現実的ではありません。具体的には、実在庫だけではなく、納入リードタイム間の発注残数と発注待ち状態にある数量も合わせて捉える必要があるのではないか。それを流動インベントリー（STI）と呼ぶことにします。

欠品の発生をある率以下にするための必要在庫量は、実は、実在庫ではなくて、流動インベントリーの大きさ（SSTI）なんです。つまり、在庫だけをみていてはダメ。SSTIの決定原理は、いたって簡単で、例えば定期発注方式では次のようになります。

SSTI＝（納入リードタイム＋発注サイクル）間の最大需要量

具体的なSSTIの計算方法については、「STIC発注方式」、「在庫管理；STICの定理」を参照ください。その時の実在庫が適正在庫となります。在庫分布およびその近似計算式を前回示したわけです。

適正在庫を維持しろ、と言われると、在庫そのものに注意が行ってしまいますが、在庫そのものをいじってもダメなんですね。発注待ち、注残もあわせて、STIとして捉え、その大きさを設定することで適正在庫が維持できるわけです。STIは常に一定であることにもご留意頂きたいと思います。これまでの在庫管理では、発注待ちや注残はわきに置かれていたんじゃないでしょうか。適正在庫を維持するうえで、STIは絶対に必要な要素なんですね。

少し、話が変わりますが、TOC（制約理論）が提唱する在庫管理方法にダイナミック・バッファー・マネジメント（Dynamic Buffer Management；DBM）というものがあります。TOCが主張する適正在庫維持管理方法です。

TOCの在庫補充は、STIC発注方式と同じで、出荷した分を補充発注する方法です。在庫と注残を合計したものを在庫バッファーと呼んでいます。（発注待ち分を含むかどうかは明示されてないようですが、流動インベントリーと概略同じとみていいと思います）図2を参照ください。

在庫バッファーを３等分して、赤、黄、青とします。在庫が赤ゾーンに入ってくると在庫バッファーを大きくして補充発注量を増やします。在庫が青ゾーンになると在庫バッファーを小さくして、補充発注量を少なくします。こうすることで在庫は中央の黄ゾーンになるように調整されます。在庫が黄ゾーンにあれば適正だ、ということになります。

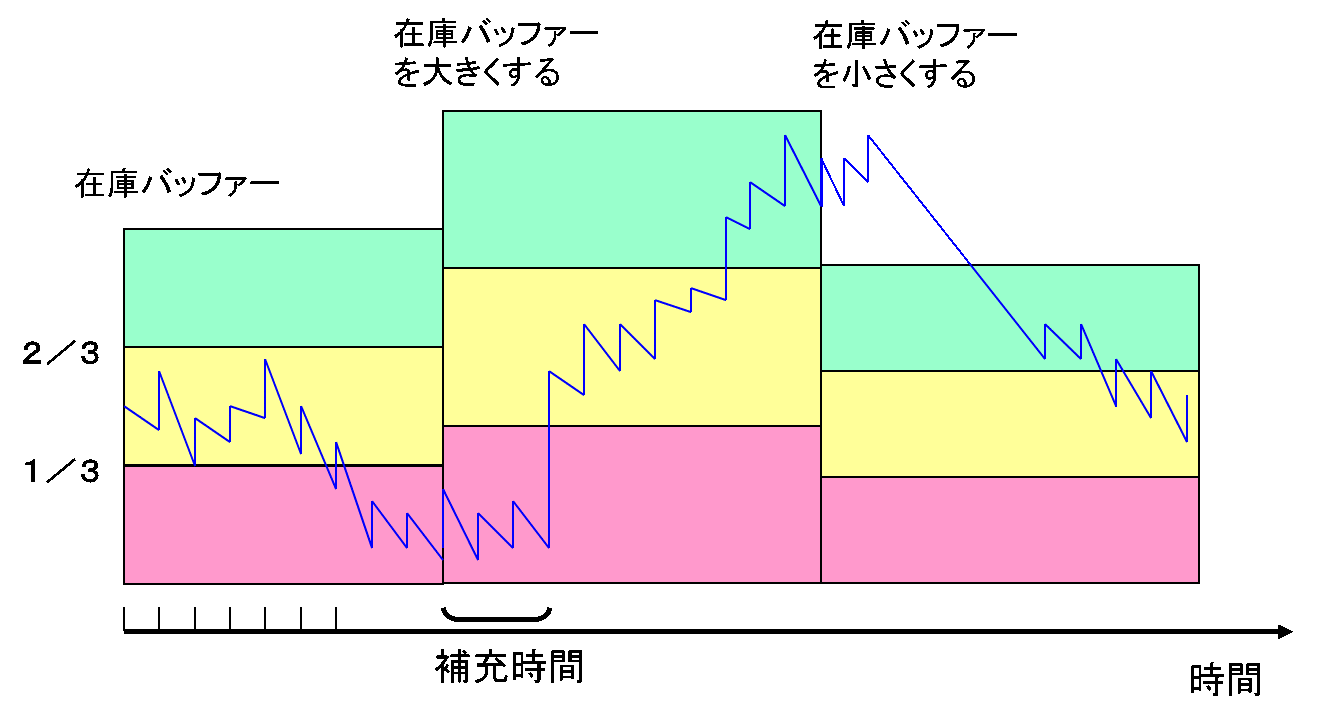
図2 ダイナミック・バッファー・マネジメントの概要

在庫レベルが赤ゾーンや青ゾーンに移動したとき、黄ゾーンになるように調整するわけですから、DBMの前提条件は、在庫の分布は在庫バッファーの中央にあるとき適正在庫状態である、としている、と考えられます。

で、在庫バッファーに対する実在庫の分布状態はどうなのか、ですが、これは前回調べたデータをみれば分かります。その中から３点、選び出して、赤、黄、青の３ゾーンを重ねたものを図3に示します。

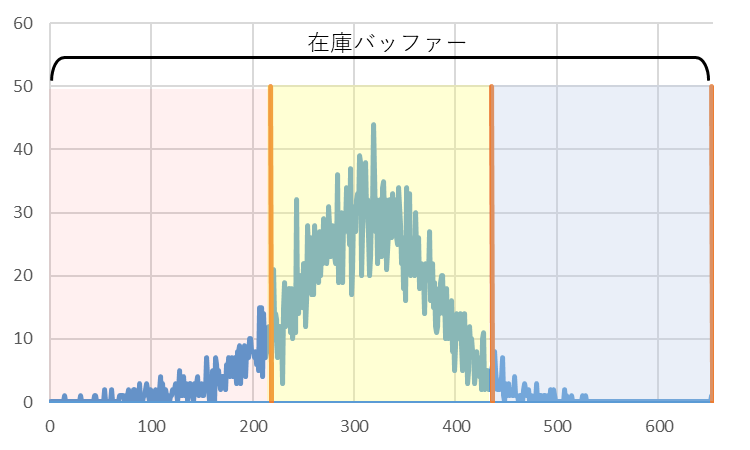
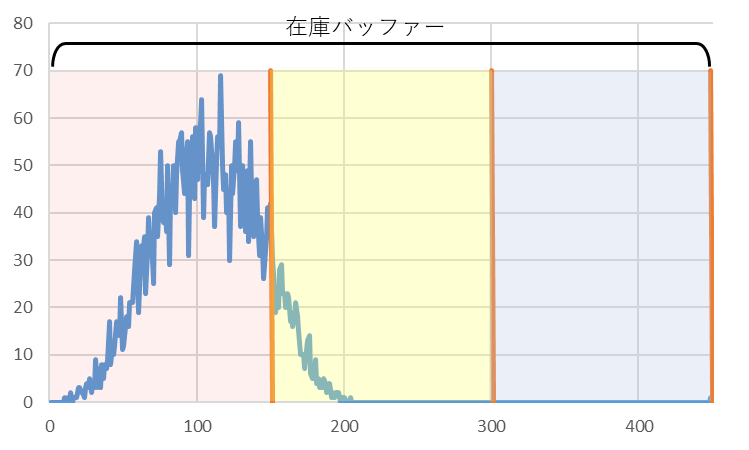
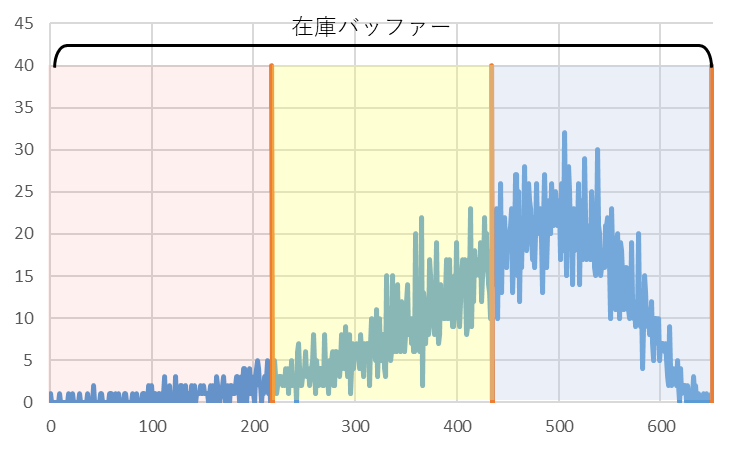
図3 在庫バッファーに対する実在庫分布のいろいろ

上段の場合はいいんでしょうが、中段や下段の場合はどうなるんでしょうか。中段の場合、在庫レベルは赤ゾーンにありますので在庫バッファーを大きくすることになります。その１例を図4に示します。在庫バッファーを大きくすると、注残、発注待ちはそのままで在庫だけが増えます。増えた在庫は余分な在庫です。適正在庫にしようとして在庫分布を中央にもってくると、無駄な在庫が増えるだけ、という結果に、、。

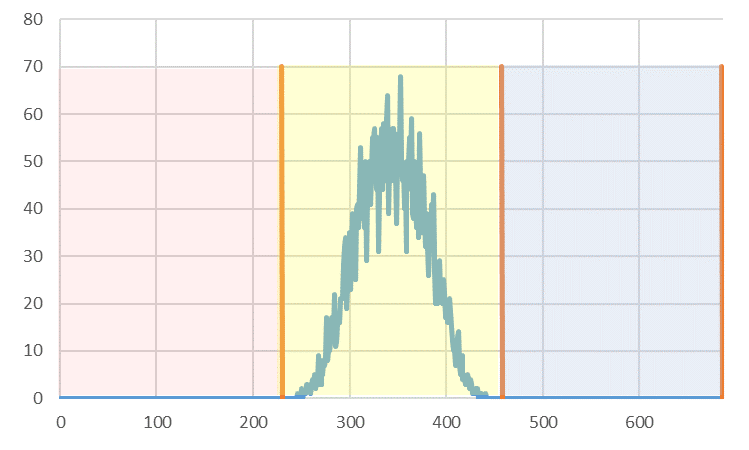
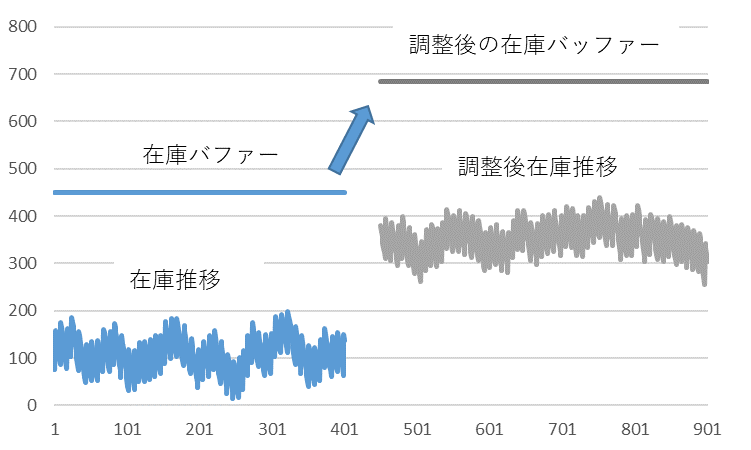
図4 在庫バッファーを大きくして在庫分布を黄ゾーンに調整する

図3の下段のような場合、在庫バッファーを小さくすると、、、今度は欠品がバカバカ出ることになります。

DBMも、在庫バッファー（流動インベントリー）と実在庫の関係を見落としているんじゃないかと思います。市販されている在庫管理用ソフトにDBMの機能を組み込んでいるものが散見されますが、お使いになるときは、お気をつけください。

じゃ、どうしたら、適正在庫を維持できるんでしょうか、、、