No.31　在庫管理統一理論；STICの定理

在庫管理は適正在庫とか発注点という基準ではなく、常に変動し、つかまえどころのない需要を基準としなければならない、と前回申し上げました。多分多くの方々は、疑問を感じられるかもしれません。変動する需要が在庫管理の基準となりうるのか？そんなことをしたら、在庫管理はますます複雑になり、難しくなるのではないか？、、と。

結論から言いますと、需要基準の在庫管理の方がはるかに簡単なんです。これまでの、適正在庫や発注点を基準とした在庫管理に慣れ親しんできた方々には、理解しにくいのは止むを得ないかもしれません。これから、ステップ・バイ・ステップで解説していきますが、部分の説明に入る前に、その要点を「STIC発注方式」と題して、まとめてみました。理論的な面に焦点を当て、論文調にまとめましたので、少々わかりづらいかもしれません。さらっと読んでいただいて、理論のイメージを思い浮かべていただければよろしいかと思います。

需要基準の在庫管理のコアになる部分は「STICの定理」です。この定理から導き出された発注方式がSTIC発注方式です。その骨子は次のようになります。

＊ 定期不定量発注；予め決められた発注間隔で、その間に受注した量を補充発注する。発注量の決定に在庫量や需要予測量は不要。
＊ 定量不定期発注；受注量が予め決めた量に達したとき、その量を補充発注する。発注点を設定する必要はない。調達リードタイムに関係なく補充発注量を決めることができるため、在庫レベルの変動は定期不定量発注と同等の滑らかさになる。
＊ 不定期不定量発注（適時適量発注あるいは即時発注）；受注時に受注した量を直ちに補充発注する。適時適量の決定は在庫管理側が決めることではなく、市場が決めること。だから、「時期も量も定まらない」。

これまでの発注方式と比べると、STIC発注方式は非常に簡単です。しかも、保持する在庫量は従来の発注方式と比べると、ほとんどのケースで少なくなります。つまり、変動する需要に基準を置いた方が、在庫管理は簡単になり、スッキリする、というわけです。

ちょっと、脱線しますが、需要に基準を置いた方が管理は簡単になるのは、在庫管理だけではありません。生産管理もそうなんです。受注生産でも見込み生産でも、あるいはその混合でも、市場の需要に基準を置いた方が管理は簡単になります。その具体的な例が「動的生産管理」です。これは、このWebsiteのメインテーマでもあります。

在庫管理と生産管理は切っても切れない関係にあります。生産管理も在庫管理も需要が基準となっている、というのは当たり前といえば当たり前です。市場に価値あるもの（製品やサービス）を提供する機能が生産管理であり在庫管理ですから市場（需要）を基準とするというのは、概念的に正しいのではないかと思います。

では、部分の説明に入りたいと思います。初めに、「需要」について考えてみます。在庫から出てゆくのは需要があるからです。需要が変動しなければ、つまり、一定の時間間隔で在庫から出てゆけば在庫管理は非常に簡単になります。ところがそうではない。変動します。しかもランダムに。ランダムに変動する需要をどう捉えるか。これが最初の課題です。

ランダムとは、ランダムの中に入るとカオスの世界で何の秩序もないようにみえますが、高所から俯瞰すると、ある規則性があることがわかります。例えば、ある店に来る客の時間間隔をみてみましょう。12:00時に一人の客が来て弁当を買いました。次の客は12時10分に来てジュースを買いました。12時16分に次の客が来てパンを買いました。夫々の時間間隔は10分、6分となります。この時間間隔はランダムにバラツクだろうと考えられます。

この時間間隔のデータを、横軸に時間間隔、縦軸に頻度をとり集計します。そうすると、店により、時間帯により異なりますが、どれも似たようなカーブになります。ランダムも見方によって規則性がみえてきます。このカーブは指数分布と呼ばれています。その一例を図1に示します。

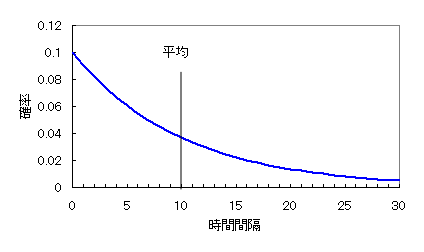
図１　平均10の指数分布の例

来客の頻度を時間間隔で捉えることは理に合っていますが、人間の感覚にはなじまないところがあります。時間間隔ではなく、ある時間、例えば1時間に何人の客が来るか、という見方もできます。平均10分間隔で客が来るのであれば、1時間では平均6人の客が来る、ということになります。1日（24時間）では平均144人、1週間では平均1,008人の客が来る、と。

製品の売れ行きをみたり、欠品しないように仕入れたりする在庫管理では、ある時間の来客数で把握するほうがわかりやすいと思います。ある時間を集計時間と呼んでおきます。来客数は集計時間にほぼ比例することがわかります。

話を一般的にまた簡単にするために、来客数を受注件数とし、商品は1種類とします。また来客一人はひとつの商品を買う、つまり受注件数と受注量は等しい、とします。正確性を期すために、最小限の数式は使わざるを得ません。ご了解ください。時間間隔の平均を、集計時間をTgとすると、受注件数の平均は次のようになります。

この式は非常に簡単です。来客（受注）の頻度を来客数（受注件数）に変換する式です。

ここまでは簡単なのですが、では、バラツキはどうなるか。受注の時間間隔がバラツキますので、集計時間での受注件数も当然バラツキます。どのような分布でバラツクのか、これを知りたいわけです。

ランダムに到着する注文がある集計時間ではどのような分布となるかは、指数分布とポアッソン分布の関係にあることが知られております。

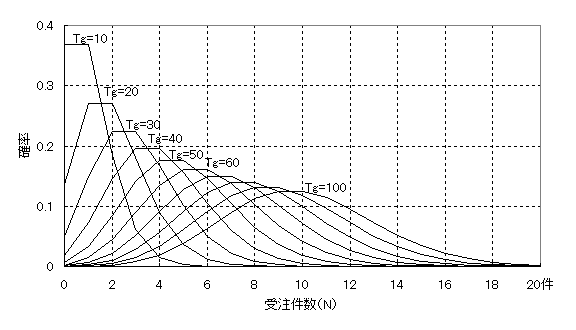
図２　受注件数の分布（ポアッソン分布）

図2は平均10の指数分布で到着する注文の分布です。集計時間Tgが10のとき、受注件数Nの平均は1ですが、分布形状は対称ではありません。Tgが50～60以上になるNの分布形状は対称形に近くなり、また正規分布に似てきます。尚、ポアッソン分布は離散型の分布です。Nは整数でその確率を示しています。

ポアッソン分布にはおもしろい性質があります。それは平均と分散が同じ、ということです。図2のTg=100のポアッソン分布の平均は10、分散も10 です。